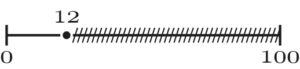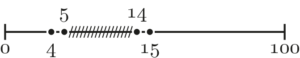Bernoulli und Binomial-Verteilung
Auf diesem Artikel bekommst du Aufgaben, Videos und Erklärungen zur Bernoulli Verteilung:
- Was ist ein Bernoulli Experiment?
- Binomialverteilung
- Typische Binomialrechnungen
- Übersicht typischer Fragestellungen
- δ-Regeln (Sigma-Regeln)
Neu!
Was ist ein Bernoulli Experiment?
Ein Bernoulli Experiment ist ein Zufallsexperiment, bei dem man sich nur dafür interessiert, ob ein Ereignis A eintritt oder nicht. Es wird also nur Erfolg oder nicht Erfolg betrachtet. Die Bernoulli Verteilung ist stets diskret!
Dann heißt $X$ bernoulliverteilt mit Parameter $p$. Man schreibt $X \sim B(1,p)$.
Es sei $p=P(A)$ die Eintritts- oder Erfolgswahrscheinlichkeit. Die Zufallsvariable $X$ kann nun folgende Werte annehmen
\begin{align*}
X=\left\{\begin{array}{ll} 1, \ \textrm{falls A eintritt} \\
0, \ \textrm{falls A nicht eintritt}
\end{array}\right. \notag
\end{align*}
und beschreibt die Anzahl der Erfolge bei $n=1$ Versuchen.
Bemerkungen
Sei $X \sim B(1,p)$. Dann ist die Wahrscheinlichkeitsfunktion:
\begin{align*}
P(X=1)=p \quad \textrm{und} \quad P(X=0)=1-p ~\textrm{Gegenwahrscheinlichkeit}
\end{align*}
Daraus ergeben sich folgende Lage- und Streuungsmaße:
1. Erwartungswert:
\begin{align*}
\mu=E(X)=p
\end{align*}
Der Erwartungswert ist hier die Eintrittswahrscheinlichkeit.
2. Varianz:
\begin{align*}
\sigma^2=V(X)=p \cdot (1-p)
\end{align*}
3. Standardabweichung:
\begin{align*}
\sigma = \sqrt{p\cdot (1-p)}
\end{align*}
Zur Erinnerung: Die Standardabweichung misst, wie schwer es ist, diese Wahrscheinlichkeit zu schätzen.
Beispiele: Geburt (Mädchen/Junge), Münzwurf (Kopf/Zahl)
Daniel rechnet für euch nochmal ein Beispiel zum Thema Bernoulli Verteilung.
Binomialverteilung
Die Binomialverteilung („mit Zurücklegen-Verteilung“) ist eine der wichtigsten diskreten Wahrscheinlichkeitsverteilungen. Eine Binomialverteilung ist die $n$-malige Wiederholung eines Bernoulli Experiments.
Dann heißt $X$ binomialverteilt mit Parametern $n$ und $p$. Man schreibt $X \sim B(n,p)$.
Bemerkungen
- Die einzelnen Wiederholungen sind stochastisch unabhängig.
- Die Erfolgswahrscheinlichkeit ist bei allen Wiederholungen $p$:
\begin{align*}
\textrm{genau }k\ \textrm{Treffer:} \ P(X=k)&= \left( \begin {array} {c} n\\ k\end{array} \right) \cdot p^k \cdot (1-p)^{n-k} \notag \\
\textrm{höchstens }k\ \textrm{Treffer:} \ P(X\leq k)&= \sum_{i=0}^k \left( \begin {array} {c} n\\ i \end{array} \right) \cdot p^i \cdot (1-p)^{n-i} \notag
\end{align*}
- Was ist eigentlich das $n$, $p$ und $k$?
$n$ = Anzahl der Ziehungen
$p$ = Wahrscheinlichkeit
$k$ = Anzahl der Treffer
- Berechnung für genau $k$ Treffer mit GTR/CAS: binompdf$(n,p,k)$
- Berechnung für höchstens $k$ Treffer mit GTR/CAS: binomcdf$(n,p,k)$
- Den Binomialkoeffizienten $\left( \begin {array} {c} n\\ k\end{array} \right)$ ermittelt man mit der nCr-Taste des Taschenrechners oder mit der Formel $\frac{n!}{k! \cdot (n-k)!}$
- Die Summe der Wahrscheinlichkeiten muss wieder 1 ergeben.
- Wichtig: Immer anwendbar beim „Ziehen mit Zurücklegen“. Bei Ziehen ohne Zurücklegen nicht (in diesem Fall ist die Pfadregel hilfreich).
Daraus ergeben sich folgende Lage- und Streuungsmaße:
- Erwartungswert: $\mu=E(X)=n\cdot p$
- Varianz: $\sigma^2=V(X)=n\cdot p \cdot (1-p)$
- Standardabweichung: $\sigma = \sqrt{\sigma^2}= \sqrt{n\cdot p \cdot (1-p)}$
Beispiel
Eine Urne enthält 6 schwarze und 4 rote Kugeln. Es werden 5 Kugeln mit Zurücklegen gezogen.
Grundlegend muss man herausfinden, um welche Verteilung es sich handelt. In der Aufgabenstellung steht, dass die Kugeln „mit Zurücklegen“ gezogen werden und daraus folgt, dass es sich um die Binomialverteilung handeln muss.
\begin{align*}
X \sim B(n,p)
\end{align*}
Jetzt müssen die Parameter $n$ und $p$ identifiziert werden, die zur Berechnung von Wahrscheinlichkeiten für die Binomialverteilung benötigt werden.
- „es wird fünf mal gezogen“: daraus folgt $n=5$.
- $p$: Laplace Wahrscheinlichkeit, also der Quotient aus den günstigen Ereignissen und den möglichen Ereignissen. Daraus folgt: $p=4/10=0,4$.
Wir fassen zusammen:
- Für rote Kugeln gilt $X \sim B(5;0,4)$.
- für schwarze Kugeln gilt $ X \sim B(5;0,6)$.
Es werden die nachstehenden Aufgaben bearbeitet.
1) Berechne den Erwartungswert der roten Kugeln:
\begin{align*}
\mu=n\cdot p=5\cdot 0,4=2
\end{align*}
2) Berechne die Varianz der roten Kugeln:
\begin{align*}
\sigma^2=n\cdot p \cdot (1-p)=5\cdot 0,4\cdot (1-0,4)=1,2
\end{align*}
3) Wie groß ist die Wahrscheinlichkeit genau drei rote Kugeln zu ziehen?
Hier gilt also $X \sim B (5;0,4)$ mit $k=3$:
\begin{align*}
P(X=3)= \left( \begin {array} {c} 5\\ 3\end{array} \right) \cdot 0,4^3 \cdot (1-0,4)^{5-3}=0,2304
\end{align*}
oder mit TR und dem Befehl binompdf$(5;0,4;3)$. Die Wahrscheinlichkeit für genau drei rote Kugeln beträgt 23,04%.
4) Wie groß ist die Wahrscheinlichkeit höchstens zwei rote Kugeln zu ziehen?
Hier gilt also $X \sim B (5;0,4)$ mit $k \leq 2$:
\begin{align*}
P(X \leq 2)&= P(X=0) + P(X=1) + P(X=2) \\
&= \left( \begin {array} {c} 5\\ 0\end{array} \right) \cdot 0,4^0 \cdot (1-0,4)^{5-0} + \left( \begin {array} {c} 5\\ 1\end{array} \right) \cdot 0,4^1 \cdot (1-0,4)^{5-1} \\ &+ \left( \begin {array} {c} 5\\ 2\end{array} \right) \cdot 0,4^2 \cdot (1-0,4)^{5-2}
= 0,68256 \approx 68,26\%
\end{align*}
oder mit TR und dem Befehl binomcdf$(5;0,4;2)$.
5) Wie groß ist die Wahrscheinlichkeit mindestens zwei schwarze Kugel zu ziehen?
Hier gilt also $X \sim B (5;0,6)$ mit $k \geq 2$. Für die Lösung gibt es zwei Möglichkeiten, wobei die zweite Alternative $(II)$ sehr viel Zeit spart und aus diesem Grund auch gewählt werden sollte!
\begin{align*}
(I) \quad P(X \geq 2)&= P(X=2) + P(X=3) + P(X=4) + P(X=5) \\
(II) \quad P(X \geq 2) &= 1- ((P(X=0) + P(X=1))
\end{align*}
Nach Einsetzen der gegebenen Werte ergibt sich die Wahrscheinlichkeit mindestens zwei schwarze Kugeln zu ziehen: $P(X \geq 2)=0,91296$.
Neu!
Typische Binomialrechnungen
Eine Stichprobe besteht aus $n=100$ Schrauben und die Wahrscheinlichkeit einer defekten Schraube liegt bei $p=0,1$.
- Gesucht sei die Wahrscheinlichkeit, dass genau $12$ Schrauben defekt sind:
\begin{align*}
P(X=12)= \left( \begin {array} {c}
100\\
12
\end{array} \right) \cdot 0,1^{12} \cdot 0,9^{100-12} \notag
\end{align*}
Also alle Wahrscheinlichkeiten von $0$ bis $12$ aufsummieren:
\begin{align*}
P(X \leq 12)&= P(X=0)+P(X=1)+…+P(X=12) \notag \\
&= F(100;0,1;12) \notag
\end{align*}
Also alle Wahrscheinlichkeiten von $12$ bis $100$ aufsummieren oder mit der Gegenwahrscheinlichkeit rechnen:
\begin{align*}
P(X \geq 12) &= \underbrace{1}_{\text{Alles}}-\underbrace{P(X \leq 11)}_{0-11} \notag
\end{align*}
- Gesucht sei die Wahrscheinlichkeit für \underline{mehr} als $4$, aber weniger als $15$ defekte Schrauben:
Also alle Wahrscheinlichkeiten zwischen 5 und 14 aufsummieren oder clever mit Gegenwahrscheinlichkeiten:
\begin{align*}
P(5 \leq X \leq 14) &= \underbrace{P(X \leq 14)}_{\text{Alles bis 14}}-\underbrace{P(X \leq 4)}_{\text{Alles bis 4}} \notag
\end{align*}
Schau dir zur Vertiefung Daniels Lernvideo zum Thema Binomialrechnung an.
Zusatzvideo mit Beispielaufgabe von Daniel
Übersicht typischer Fragestellungen
\begin{align*}
\text{genau} \ \ k \ \ \text{Treffer} : \ \ &P(X=k)= \left( \begin {array} {c} n\\ k\end{array} \right) \cdot p^k \cdot (1-p)^{n-k} \notag \\
\text{höchstens} \ \ k \ \ \text{Treffer} : \ \ &P(X \leq k) \notag \\
\text{weniger als} \ \ k \ \ \text{Treffer} : \ \ &P(X < k)=P(x\leq k-1) \notag \\
\text{mindestens} \ \ k \ \ \text{Treffer} : \ \ &P(X \geq k) = 1- P(x \leq k-1)\notag \\
\text{mehr als} \ \ k \ \ \text{Treffer} : \ \ &P(X > k) = 1-P(x \leq k) \notag \\
\text{mind.} \ k, \ \text{aber höchst.} \ \ h \ \ \text{Treffer} : \ \ &P(k \leq X \leq h) = P(X \leq h) – P(X \leq k-1) \notag
\end{align*}
Oft wird auch nach der Anzahl der Ziehungen/Wiederholungen $n$ gefragt. Dabei gibt es einige Dinge zu beachten. Machen wir uns das Ganze anhand eines Beispiels klar:
Wie viele Bälle müsste man mindestens kontrollieren, um mit einer Wahrscheinlichkeit von mindestens 95% wenigstens einen fehlerhaften Ball zu finden? $X$ sei binomialverteilt mit $p=0,1$. Gesucht ist demnach $n$.
Es gilt:
\begin{align*}
\begin{array}{crcll}
&P(X \geq 1) &\geq& 0,95 & \\
\Leftrightarrow &1-P(X=0) &\geq& 0,95 & |+P(X=0) ~ |-0,95 \\
\Leftrightarrow &0,05 &\geq& P(X=0) & \\
\Leftrightarrow &P(X=0) &\leq& 0,05 & | ~\textrm{Formel einsetzen} \\
\Leftrightarrow &\left( \begin {array} {c} n\\ 0\end{array} \right) \cdot 0,1^0 \cdot 0,9^n &\leq& 0,05 & | ~\textrm{bel. Zahl hoch 0 ist immer 1} \\
\Leftrightarrow &0,9^n &\leq& 0,05 & | ~\textrm{beide Seiten logarithmieren} \\
\Leftrightarrow &\ln (0,9^n) &\leq& \ln(0,05) & | ~\textrm{Logarithmengesetze} \\
\Leftrightarrow &n \cdot \ln (0,9) &\leq& \ln(0,05) & |~\textrm{ln(0,9) negativ, daher Vorzeichenumkehr} \\
\Leftrightarrow &n &\geq& \frac{\ln (0,05)}{\ln (0,9)} \approx 28,43 &
\end{array}
\end{align*}
Es müssten somit mindestens $29$ Bälle kontrolliert werden, um wenigstens einen fehlerhaften Ball zu finden.
Beachtet: Bei mal oder durch $(-1)$ dreht sich das größer oder kleiner Zeichen. Wenn wir durch den $\ln$ teilen, müsst ihr aufpassen ob der $\ln$ eventuell negativ ist, dann dreht sich das Zeichen wieder.
δ-Regeln (Sigma-Regeln)
Bei der Binomialverteilung konzentrieren sich die Werte um den Erwartungswert $\mu$. Deshalb untersucht man häufig symmetrische Umgebungen um den Erwartungswert. Den Radius dieser Umgebungen gibt man meist als Vielfaches der Standardabweichung $\sigma$ an. So ist z.B. die $2\sigma$-Umgebung des Erwartungswerts das Intervall $[\mu-2\sigma;\mu+2\sigma]$.
Beispiel
Sei $X \sim B(50;0,3)$. Bestimme die $2\sigma$-Umgebung und die Wahrscheinlichkeit dafür, dass $X$ in dieser Umgebung liegt.
Mit dem Erwartungswert $\mu = 50 \cdot 0,3= 15$ und der Standardabweichung $\sigma=\sqrt{50\cdot 0,3 \cdot 0,7}=3,24$ ergibt sich das Intervall
\begin{align*}
[15-2\cdot 3,24 ; 15 + 2 \cdot 3,24] = [8,52 ; 21,48]
\end{align*}
und die Werte liegen (da diskrete Verteilung, also nur ganze Zahlen) zwischen 9 und 21. Die Wahrscheinlichkeit lautet dann
\begin{align*}
P(9\leq X\leq 21)=P(X \leq 21)−P(X \leq 8)=\sum_{k=9}^{21} \begin{pmatrix}
50 \\ k
\end{pmatrix} 0,3^k \cdot 0,7^{50−k}=0,9566.
\end{align*}
Wir sehen, dass die Berechnung der obigen Wahrscheinlichkeit sehr umständlich ist. Aus diesem Grund wurden für die am häufigsten verwendeten $\sigma$-Umgebungen sogenannte $\sigma$-Regeln eingeführt, die die zugehörigen Wahrscheinlichkeiten näherungsweise bestimmen. Für eine binomialverteilte Zufallsvariable $X \sim B(n,p)$ werden in der $\sigma$-Umgebung gute Werte erzielt, falls die Laplace-Bedingung $\sigma>3$ erfüllt ist.
Wahrscheinlichkeit in $\sigma$-Umgebung, falls $\sigma>3$:
\begin{align*}
P(\mu-\sigma \leq X \leq \mu + \sigma) \ &\approx \ 0,68 \\
P(\mu- 1,64 \sigma \leq X \leq \mu + 1,64 \sigma) \ &\approx \ 0,90 \\
P(\mu- 1,96 \sigma \leq X \leq \mu + 1,96 \sigma)\ &\approx \ 0,95 \\
P(\mu- 2 \sigma \leq X \leq \mu +2 \sigma) \ &\approx \ 0,955 \\
P(\mu- 2,58 \sigma \leq X \leq \mu + 2,58 \sigma)\ &\approx \ 0,99 \\
P(\mu- 3\sigma \leq X \leq \mu + 3 \sigma) \ &\approx \ 0,997 \\
\end{align*}
Woher diese Werte wie 0,68 oder 0,997 kommen, sehen wir bei der Dichtefunktion der Normalverteilung.
Neu!