Die Technische Biegetheorie
Du willst wissen wie du bei der Berechnung von Biegung vorgehen musst? In diesem Artikel geben wir dir Erklärungen zu folgenden Themen:

19,99€
Gerade Biegung ohne Normalkraft
$\rightarrow$ Lastebene = Verformungsebene
Voraussetzungen:
- $S_y=0$: $x$-Achse durch den Schwerpunkt verläuft
- $I_{yz}=0$: Querschnitt hat mindestens eine Symmetrieachse
Formeln:
\begin{align*}
\sigma(x,z)&= \frac{M_y(x)}{I_y} \cdot z \quad \textrm{„Normalspannung“} \\
w“(x) &= – \frac{M_y(x)}{EI_y} \quad \textrm{„Biegelinie“}
\end{align*}
mit $z$ als maximalen Randfaserabstand und $E\cdot I_y$ als Biegesteifigkeit.
Lösungsschritte (vgl. Rolf Mahnken, Lehrbuch der Technischen Mechanik – Elastostatik, Springer Verlag, 1. Auflage, 2015)
(i) für statisch bestimmte Systeme
a. Statisches System
b. Schnittgrößen mittels Gleichgewicht am geschnittenen System $\rightarrow$ TM 1, wobei häufig nur $M_y(x)$ benötigt wird!
c. Querschnittswerte
1. Berechnung der Schwerachse, so dass $S_y=0$ gilt.
2. Überprüfung, ob mindestens eine Symmetrieachse vorliegt, so dass $I_{yz}=0$– Wenn keine Symmetrieachse vorliegt, hat man schiefe Biegung!
3. $I_y$ berechnen.
d. Normalspannungen: maximale Spannung in Randfläche mit größtem Abstand $|z|_{max}$
e. Biegelinie
1. $M_y(x)$ als Funktion der Koordinate $x$ für $n$ Einzelbalken
2. $2 \cdot n$ Rand- und Übergangsbedingungen für $w(x)$ und $\varphi(x)$
3. Integration der Differentialgleichung $w“(x)=-\frac{M_y(x)}{EI_y}$
f. weitere Aufgabenstellungen, z.B. Spannungs-/Verformungsnachweis, Bauteilsicherheit etc.
(iI) für statisch unbestimmte Systeme
a. Statisches System
b. Querschnittswerte
1. Berechnung der Schwerachse, so dass $S_y=0$ gilt.
2. Überprüfung, ob mindestens eine Symmetrieachse vorliegt, so dass $I_{yz}=0$– Wenn keine Symmetrieachse vorliegt, hat man schiefe Biegung!
3. $I_y$ berechnen.
c. Biegelinie, unter Beachtung von $4\cdot n$ Rand- und Übergangsbedingungen für $w(x), \ p(x), \ M_y(x), \ Q_z(x)$ berechnet man für jeden Einzelbalken:
\begin{align*}
EI_y w^{IV}(x)=q_z(x)
\end{align*}
d. weitere Aufgabenstellungen, z.B. $M_y(x)=-EI_y w“(x), \ \sigma(x,y,z) = \frac{M_y(x)}{I_y} \cdot z$, Dimensionierung etc.
Kochrezept bei Aufgaben zum Biegebalken
Vorgehen bei statisch unbestimmten Systemen
Beispiel Biegung ohne Normalkraft
Gerade Biegung mit Normalkraft
- gleichgültig ob statisch bestimmt oder unbestimmt!
- Vorgehen gemäß jeweiligen Lösungsschritten von oben
- Resultierende Verschiebungen und Spannungen über Superposition
- Voraussetzung: $S_y=0$; $I_{yz}=0$
Formeln
1. Normalspannung: $\sigma(x,z)= \frac{N(x)}{A(x)} + \frac{M_y(x)}{I_y} \cdot z$
2. Verschiebung: $EAu'(x)=N(x); \ EI_yw“(x)=M_y(x); \ f=\sqrt{u^2 + w^2}$
3. Gleichgewicht: $N'(x)=-n(x); \ M_y“(x)=-q_z(x)$
Schiefe Biegung
$\rightarrow$ Lastebene $\neq$ Verformungsebene
- Belastung schräg zur Symmetrieachse oder bei unsymmetrischen Querschnitten
- Auch hier gibt es statisch bestimmte und unbestimmte Systeme!
Insgesamt sind 4 Fälle zu unterscheiden:
1. Koordinatensystem im Schwerpunkt
$\rightarrow \ S_y=S_z=0$
$\bullet$ Normalspannung:
\begin{align*}
\sigma(x,z) &= \frac{N(x)}{A(x)} + \frac{M_y(x) \cdot I_{yz} – M_z (x) \cdot I_y}{\Delta} \cdot y + \frac{M_y(x) \cdot I_{z} – M_z (x) \cdot I_{yz}}{\Delta} \cdot z \\
\textrm{mit} \ \Delta &= I_y \cdot I_z – I_{yz}^2
\end{align*}
$\bullet$ Verschiebungen:
\begin{align*}
u'(x) &= \frac{N(x)}{EA(x)} \\
w“(x) &= – \frac{M_y(x) \cdot I_z}{E\Delta} + \frac{M_z(x)\cdot I_{yz}}{E \Delta} \\
v“(x) &= – \frac{M_y(x) \cdot I_{yz}}{E\Delta} + \frac{M_z(x)\cdot I_{y}}{E \Delta}
\end{align*}
$\bullet$ Resultierende Verschiebung: $f= \sqrt{u^2 + v^2 + w^2}$
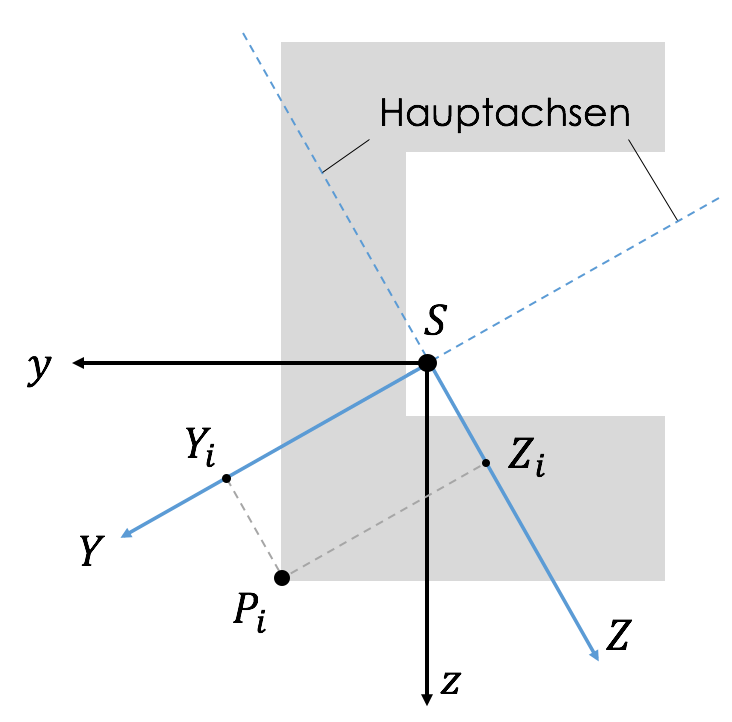
2. Transformation auf Hauptachsen
$\rightarrow$ In Hauptachsen sind $I_y, \ I_z$ maximal und $I_{yz}=0$
(i) Berechnung der Hauptträgheitsmomente $I_Y, \ I_Z$ und der Hauptachsen mit den Winkeln $\alpha_Y^*, \ \alpha_Z^*$
(ii) Transformation der Momente $M_y, \ M_z$ und der Koordinaten bestimmter Punkte auf Hauptachsensystem $Y-Z$.
\begin{align*}
M_Y &= M_y \cdot \cos \alpha_Y^* + M_z \cdot \sin \alpha_Y^* \\
Y_i &= y_i \cdot \cos \alpha_Y^* + z_i \cdot \sin \alpha_Y^* \\
M_Z &= M_z \cdot \cos \alpha_Y^* – M_y \cdot \sin \alpha_Y^* \\
Z_i &= z_i \cdot \cos \alpha_Y^* – y_i \cdot \sin \alpha_Y^*
\end{align*}
$\bullet$ Normalspannung: $\sigma(x,Y,Z)= \frac{N(x)}{A(x)} + \frac{M_Y(x)}{I_Y}\cdot Z -\frac{M_Z(x)}{I_Z}\cdot Y$
$\bullet$ Verschiebungen:
\begin{align*}
u'(x) &= \frac{N(x)}{EA(x)} \\
W“(x) &= – \frac{M_Y(x) }{E I_Y} \\
V“(x) &= \frac{M_Z(x)}{E I_Z}
\end{align*}
Fazit: Berechnung der Spannungen und Verschiebungen wesentlich einfacher, wenn man vorher auf die Hauptachsen transformiert!
3. Koordinatenachsen sind gleichzeitig Hauptachsen
$\rightarrow$ $S_y=0, \ I_{yz}=0$
$\bullet$ Normalspannung: $\sigma(x,y,z)= \frac{N(x)}{A(x)} + \frac{M_y(x)}{I_y}\cdot z -\frac{M_z(x)}{I_z}\cdot y$
$\bullet$ Verschiebungen:
\begin{align*}
u'(x) &= \frac{N(x)}{EA(x)} \\
w“(x) &= – \frac{M_y(x) }{E I_y} \\
v“(x) &= \frac{M_z(x)}{E I_z}
\end{align*}
$\bullet$ Charakteristische Winkel
$\bullet$ $\alpha_M$ $\rightarrow$ Winkel des resultierenden Momentes. Formel:
\begin{align*}
\tan \alpha_M = \frac{M_z}{ M_y}
\end{align*}
$\bullet$ $\alpha_N$ $\rightarrow$ Winkel der Spannungsnulllinie. Formel:
\begin{align*}
\sigma_x&=0 \\
\Rightarrow \quad z&= \frac{M_z}{M_y} \cdot \frac{I_y}{I_z}\cdot y \\
\Rightarrow \quad \tan \alpha_N&= \frac{z}{y} = \frac{M_z}{M_y} \cdot \frac{I_y}{I_z}\cdot y
\end{align*}
4. Gerade Biegung ohne Normalkraft
$\rightarrow$ $y-z$-Hauptachsen im Schwerpunkt; $N(x)=0, \ S_y=S_z=0, \ I_{yz}=0$
$\bullet$ Fall 1: $M_z(x)=0$ (Vergleich Gerade Biegung)
\begin{align*}
\sigma(x,z)&= \frac{M_y(x)}{I_y} \cdot z \\
w“(x) &= – \frac{M_y(x)}{EI_y} \\
v(x)&=0
\end{align*}
$\bullet$ Fall 2: $M_y(x)=0$
\begin{align*}
\sigma(x,y)&= -\frac{M_z(x)}{I_z} \cdot y \\
v“(x) &= – \frac{M_z(x)}{EI_z} \\
w(x)&=0
\end{align*}
Vorgehen bei schiefer Biegung

19,99€