
Binomische Formeln
Es gibt drei binomische Formeln. Diese sind ein wichtiges Hilfsmittel zur Vereinfachung von Termen und können in beiden Richtungen angewendet werden. Das bedeutet, dass sie sowohl zum Ausklammern, als auch zum Faktorisieren verwendet werden können.
Was dich auf dieser Seite erwartet:
- Wie lauten die drei binomischen Formeln?
- Erste binomische Formel
- Zweite binomische Formel
- Dritte binomische Formel
- Wofür brauche ich die binomischen Formeln?
Wie lauten die drei binomischen Formeln?
- Binomische Formel: $ \mathbf{(a+b)^2} = a^2+2 \cdot a \cdot b + b^2 \\ \\ $
- Binomische Formel: $ \mathbf{(a-b)^2} = a^2-2 \cdot a \cdot b + b^2 \\ \\ $
- Binomische Formel: $ \mathbf{(a+b)\cdot(a-b)} = a^2-b^2 $
Erste binomische Formel
\begin{align*}
\mathbf{\left(a+b\right)^2=a^2+2\cdot a\cdot b+b^2}
\end{align*}
Wer sich mit dem Thema Ausklammern befasst hat, kann hier getrost zur 2. binomischen Formel springen. Für alle anderen macht es Sinn sich die Herleitung genauer anzuschauen:
\begin{align*}
(a+b)^2 &= (a+b)\cdot (a+b) \\
&= a\cdot(a+b)+b\cdot(a+b) \\
&= a\cdot a+a\cdot b+b\cdot a+b\cdot b \\
&= a^2+a\cdot b+a\cdot b+b^2 \\
&= a^2+2\cdot a\cdot b+b^2
\end{align*}
Der genaue Beobachter sieht, dass es sich schlicht um das Ausklammern des linken Ausdrucks handelt.
![]()
Da die ganzen Buchstaben viele Leser verwirren, zeigen wir euch das Ganze nochmal anhand von Beispielen.
Grafische Herleitung der ersten binomischen Formel
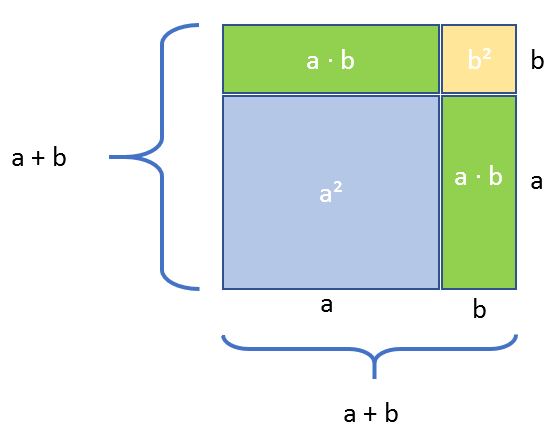
Wie man anhand der Grafik erkennen kann, ist die Seitenlänge des Quadrats a + b. Für die Berechnung des Flächeninhalts dieses Quadrats erhält man folglich $(a + b)²$. Wir können auch händisch alle Flächeninhalte zusammenzählen und erhalten: $a²+ab+ab+b² = a²+2ab+b²$
Beispiele zur ersten binomischen Formel
Beispiel 1
\begin{align*}
\left(2+3\right)^2=2^2+2\cdot 2\cdot 3+3^2=25
\end{align*}
Wie ihr sicher schon erkannt habt, ist das Ergebnis nichts anderes als $5^2$. Doch so einfach machen es euch dann die Lehrer doch nicht, wenn es um binomische Formeln geht. Oftmals werden dann Buchstaben in die Formel eingefügt, wie ihr im Beispiel 2 jetzt sehen werdet.
Beispiel 2
\begin{align*}
\left(2x+3\right)^2={\left(2x\right)}^2+2\cdot 2x\cdot 3+3^2={4x}^2+12x+9
\end{align*}
Die Vorgehensweise ist also recht einfach. Setzt für a und b einfach die entsprechenden Zahlen oder Buchstaben ein und rechnet den oben gezeigten Weg durch.
Hinweis
Der jeweils mittlere Teil der binomischen Formeln muss selbstverständlich nicht bei jeder Aufgabe mit geschrieben werden. Er dient hier nur zur Veranschaulichung und zum besseren Verständnis. Nach einiger Übung werdet ihr sicherlich in der Lage sein, direkt von der Klammer zum endgültigen Term oder umgekehrt zu gelangen.
Zweite binomische Formel
Die zweite binomische Formel sieht auf den ersten Blick viel komplizierter aus, als sie eigentlich ist. Im Gegensatz zur ersten binomischen Formel ändert sich hier nur das Vorzeichen in der Klammer.
\begin{align*}
\left(a-b\right)^2 &= \left(a-b\right)\cdot \left(a-b\right) \\
&= a\cdot(a-b) – b\cdot(a-b)\\
&= a\cdot a – a\cdot b – b\cdot a -b\cdot(-b) \\
&= a^2 – a\cdot b – a\cdot b + b\cdot b\\
&= a^2 -2\cdot a\cdot b + b^2
\end{align*}
Grafische Herleitung der zweiten binomischen Formel
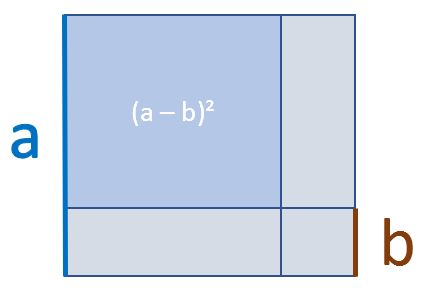
Wir nähern uns von hinten an die 2. binomische Formel an und versuchen die Fläche (a – b)² zu erreichen. Wir gehen also erstmal nur davon aus, dass wir die Seitenlängen $a$ und $b$ haben.
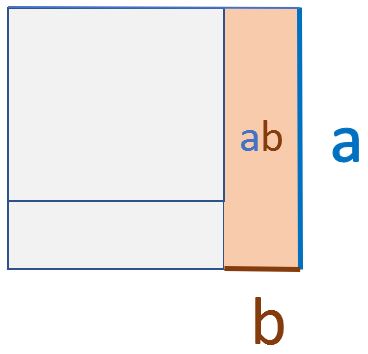
Wie wir sehen, hat das gesamte Quadrat den Flächeninhalt a². Im ersten Schritt ziehen wir die rote Fläche von a² ab und erhalten $a^2- a \cdot b$.
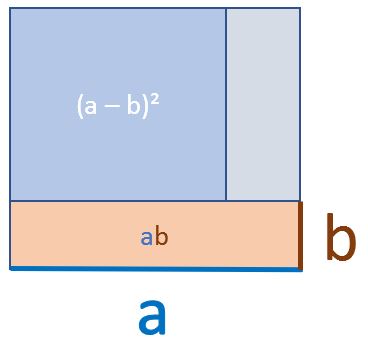
Als nächstes ziehen wir nochmals die Fläche $a \cdot b$ von $a^2- a \cdot b$ ab und erhalten $a^2 – a \cdot b + a \cdot b$. Zusammengefasst also $a^2 – 2\cdot a \cdot b$.
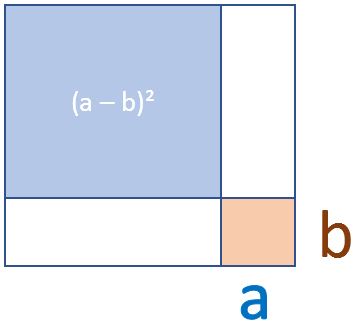
Der genaue Beobachter stellt fest, dass wir das kleine Quadrat $b^2$ unten rechts einmal zu viel abgezogen haben. Deswegen rechnen wir es einfach nochmal „drauf“ und erhalten letztendlich den finalen Ausdruck: $a^2 – a \cdot b + a \cdot b + b^2$.
Auch hier geben wir euch nochmal ein Beispiel zur Vertiefung:
Beispiel zur zweiten binomischen Formel
\begin{align*}
\left(2x-3\right)^2={\left(2x\right)}^2-2\cdot 2x\cdot 3+3^2={4x}^2-12x+9
\end{align*}
Nicht verstanden? Daniel erklärt euch die zweite binomische Formel nochmal in einem seiner Videos.
Dritte binomische Formel
Die letzte binomische Formel zeigt euch, wie ihr zwei Klammern miteinander multipliziert – sprich, hier passiert nichts anderes als einfache Klammerrechnung. Beim Hinschauen fällt direkt auf, dass in der ersten Klammer ein + und in der zweiten Klammer ein – steht.
\begin{align*}
(a+b)(a-b) &= (a+b)\cdot(a-b) \\
&= a\cdot (a-b)+b\cdot (a-b)\\
&= a\cdot a-a\cdot b+b\cdot a+b\cdot (-b) \\
&= a^2-a\cdot b+a\cdot b-b\cdot b \\
&= a^2-b^2
\end{align*}
Grafische Herleitung der dritten binomischen Formel
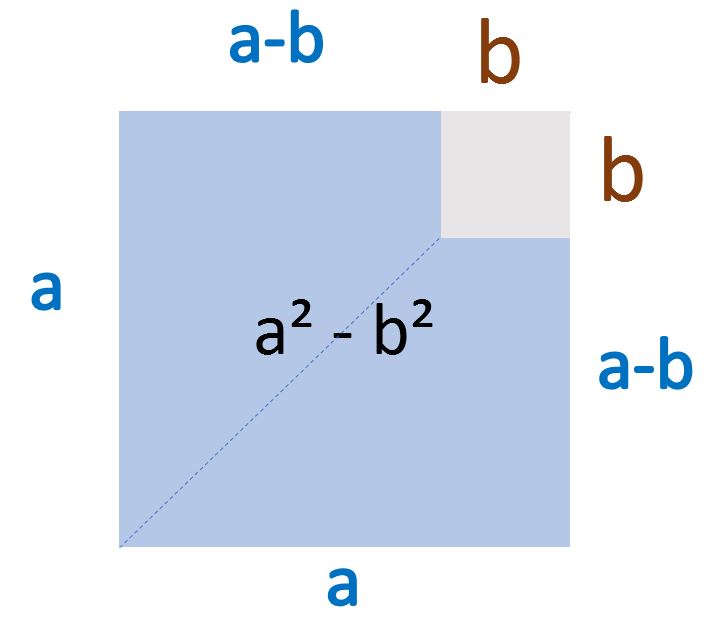
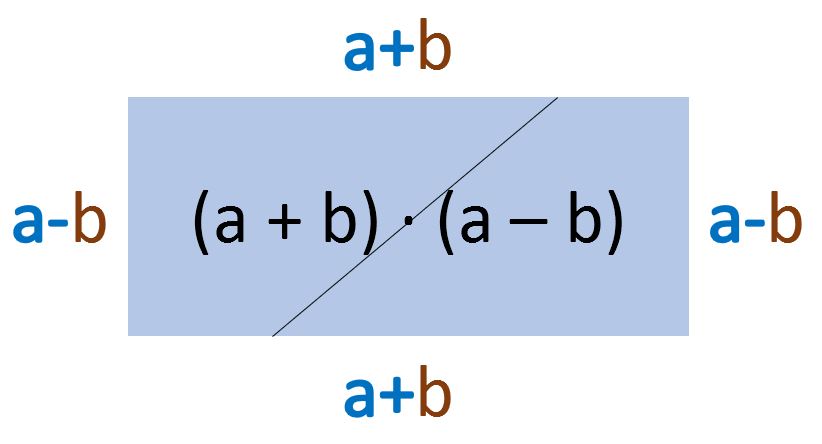
Zum Abschluss habt ihr hier noch einmal ein Beispiel zur dritten binomischen Formel.
Beispiel
\begin{align*}
\left(2x+3\right)\cdot \left(2x-3\right)={\left(2x\right)}^2-3^2={4x}^2-9
\end{align*}
Zur Wiederholung könnt ihr euch dieses Video zur dritten binomischen Formel anschauen.
Wofür brauche ich die binomischen Formeln?
- .. um Klammern schneller und leichter ausmultiplizieren zu können.
- .. zur rückgängigen Ausmultiplizierung. Sprich: Klammern erzeugen.
- .. zur Umformung von Gleichungen.
- .. zur erleichterten Rechnung mit Potenzen.
