Flächen und Flächenberechnung
Nachfolgend seht ihr die wichtigsten Figuren mit ihren Eigenschaften und den dazugehörigen Formeln. Hinweis: Der Umfang $U$ ist die Summe aller außen liegenden Seiten. Wir besprechen nachfolgend diese Themen:
- Übersicht zur Flächenberechnung
- Quadrat
- Quadrat
- Rechteck
- Trapez
- Parallelogramm
- Zusammengesetze Flächen
- Beispielaufgaben
Übersicht zur Flächenberechnung
Quadrat
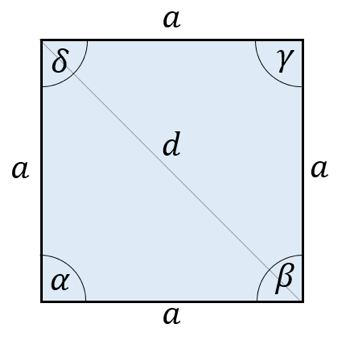
Eigenschaften:
- Alle Seiten sind gleich lang
- $\mathrm{\alpha}\mathrm{=}\mathrm{\beta}\mathrm{=}\mathrm{\gamma }\mathrm{=}\mathrm{\delta}\mathrm{=90{}^\circ }$
- Winkelsumme: $\mathrm{\alpha}\mathrm{+}\mathrm{\beta}\mathrm{+}\mathrm{\gamma}\mathrm{+}\mathrm{\delta}\mathrm{=360{}^\circ }$
Formeln:
- Umfang: $\mathrm{U=4}\mathrm{\cdot }\mathrm{a}$
- Flächeninhalt: $\mathrm{A=a}\mathrm{\cdot }\mathrm{a=}{\mathrm{a}}^{\mathrm{2}}$
- Diagonale: $\mathrm{d=a}\mathrm{\cdot }\sqrt{\mathrm{2}}$
Rechteck
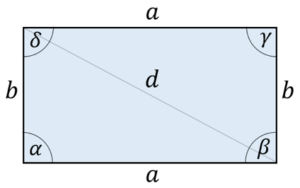
Eigenschaften:
- Die jeweils gegenüberliegenden Seiten sind gleich lang
- $\mathrm{\alpha}\mathrm{=}\mathrm{\beta}\mathrm{=}\mathrm{\gamma }\mathrm{=}\mathrm{\delta}\mathrm{=90{}^\circ }$
- Winkelsumme: $\mathrm{\alpha}\mathrm{+}\mathrm{\beta }\mathrm{+}\mathrm{\gamma}\mathrm{+}\mathrm{\delta}\mathrm{=360{}^\circ }$
Formeln:
- Umfang: $\mathrm{U=2}\mathrm{\cdot }\mathrm{a+2}\mathrm{\cdot }\mathrm{b}$
- Flächeninhalt: $\mathrm{A=a}\mathrm{\cdot }\mathrm{b}$
- Diagonale: $\mathrm{d=}\sqrt{{\mathrm{a}}^{\mathrm{2}}\mathrm{+}{\mathrm{b}}^{\mathrm{2}}}$
NEU
Trapez
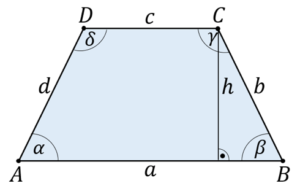
Eigenschaften:
- $\mathrm{a}\mathrm{\parallel }c$
- Winkelsumme: $\alpha \mathrm{+}\beta \mathrm{+}\gamma \mathrm{+}\delta \mathrm{=360{}^\circ }$
Formeln:
- Umfang: $U\mathrm{=a+}b\mathrm{+}c\mathrm{+}d$
- Flächeninhalt: $A\mathrm{=}\frac{\mathrm{(}a\mathrm{+}c\mathrm{)}\mathrm{\cdot }h}{\mathrm{2}}\mathrm{\ }$ oder $\frac{\mathrm{1}}{\mathrm{2}}\mathrm{\cdot }\mathrm{(}a\mathrm{+}c\mathrm{)}\mathrm{\cdot }h$
Parallelogramm
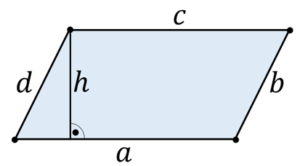
Eigenschaften:
- $\mathrm{a}\mathrm{\parallel }\mathrm{c}$
- $\mathrm{b}\mathrm{\parallel }\mathrm{d}$
- Winkelsumme: $\mathrm{\alpha}\mathrm{+}\mathrm{\beta }\mathrm{+}\mathrm{\gamma}\mathrm{+}\mathrm{\delta}\mathrm{=360{}^\circ }$
Formeln:
- Umfang: $U=a+b+c+d$
- Flächeninhalt: $A=g\cdot h$
NEU
Dreieck
Eigenschaften:
- Winkelsumme: $\alpha +\beta +\gamma =180{}^\circ $
Formeln:
- Umfang: $U=a+b+c$
- Flächeninhalt: $A=\frac{1}{2}\cdot g\cdot h$
Die Grundseite und die Höhe müssen senkrecht zueinander liegen. In unserem Fall wäre die Grundseite die Seite $c$.
Kreis
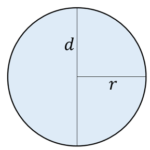
Formeln:
- Radius: $r$
- Durchmesser: $d=2\cdot r$
- Umfang: $U=2 \cdot \pi \cdot r=\pi \cdot d$
- Flächeninhalt: $A=\pi \cdot r^2$
NEU
Zusammengesetzte Flächen
Natürlich kann es auch passieren, dass unterschiedliche Flächen miteinander kombiniert werden. Eure Aufgabe ist es in diesem Fall, selbstständig eine sinnvolle Unterteilung in euch bekannte Flächen durchzuführen. Dazu wollen wir uns das folgende Beispiel einmal angucken:
Um eine solche Fläche berechnen zu können, ist es nötig, diese vorher zu unterteilen. Hier kann das auf zwei verschieden Arten passieren:
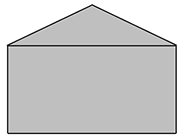
Wie auf dem Bild oben zu sehen ist, haben wir die Fläche in uns zwei bekannte Flächen unterteilt, zum einen in ein Dreieck und zum anderen in ein Rechteck. Für diese beiden Flächen können wir nun die uns bekannten Formeln zur Berechnung anwenden.
Es gibt auch noch eine weitere Möglichkeit der Unterteilung:
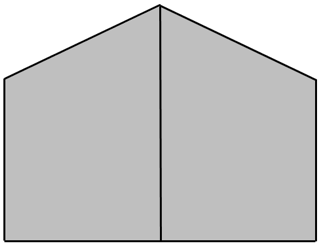
In diesem Fall haben wir die Fläche in zwei gleich große Trapeze unterteilt, deren Flächeninhalt wir nun wieder mit der uns bekannten Formel berechnen können.
Beispielaufgaben
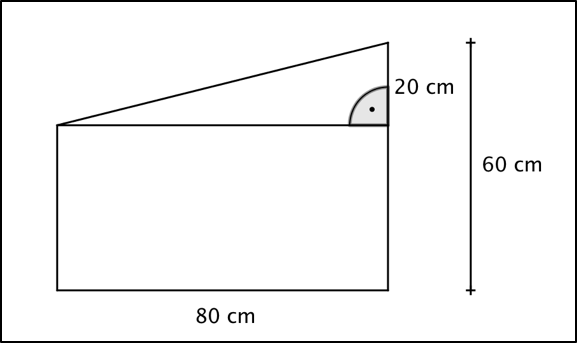
Beispielaufgabe 1 – Zusammengesetze Flächen
Berechne den Flächeninhalt der zusammengesetzten Fläche und gib das Ergebnis in an.
Lösung:
Bei der zusammengesetzten Figur handelt es sich um ein Rechteck (unterer Teil) und um ein rechtwinkliges Dreieck (oberer Teil). Wir berechnen jetzt unabhängig voneinander zuerst den Flächeninhalt des Rechtecks und danach den des Dreiecks. Anschließend werden beide Flächeninhalte addiert und wir erhalten das Gesamtergebnis.
Flächeninhalt Rechteck:
Ganz allgemein gilt für den Flächeninhalt eines Rechtecks immer:
\begin{align*}
A = a \cdot b
\end{align*}
Unser Rechteck hat eine Breite von $80\ cm$. Die Länge bzw. die Höhe unseres Rechtecks erhalten wir durch die folgende Nebenrechnung:
\begin{align*}
60 \ cm − 20\ cm= 40 \ cm
\end{align*}
Jetzt müssen wir unsere beiden Werte nur noch in die Flächeninhaltsformel einsetzen:
\begin{align*}
A=80 cm \cdot 40 cm = 3200 cm^2
\end{align*}
Letztlich müssen wir noch unser Ergebnis in die geforderte Einheit $m^2$ umwandeln:
\begin{align*}
3200cm^2 &= 3200\cdot 1 cm^2 = 3200\cdot \frac{1 dm^2}{100} = 32dm^2 \\
32dm^2 &=32\cdot 1 dm^2 = 32\cdot \frac{1 m^2}{100} = 0{,}32m^2
\end{align*}
Die Fläche unseres Rechtecks hat also eine Größe von $0{,}32m^2$.
Flächeninhalt Dreieck:
Den Flächeninhalt eines Dreiecks berechnet man allgemein mit der folgenden Formel
\begin{align*}
A=\frac{1}{2}\cdot g\cdot h
\end{align*}
In jedem rechtwinkligen Dreieck lassen sich die Grundseite und die Höhe besonders leicht identifizieren. Es handelt sich dabei immer um die beiden Seiten, welche den rechten Winkel bilden. In unserem Fall sind diese beiden Seiten $80\ cm$ und $20\ cm$ lang. Wir setzen unsere Werte in die Formel ein und erhalten:
\begin{align*}
A=\frac{80cm\cdot20cm}{2} = \frac{1600cm^2}{2} = 800cm^2 = 0{,}08m^2
\end{align*}
Zusammengesetzter Flächeninhalt:
Jetzt müssen, wie vorher schon beschrieben, beide Flächeninhalte addiert werden:
\begin{align*}
0{,}32\ cm^2 + 0{,}08\ cm^2 = 0{,}40\ cm^2
\end{align*}
Der gesamte Flächeninhalt hat eine Größe von $0{,}40\ cm^2$.
NEU
Beispielaufgabe 2 – Geometrie Winkelberechnung
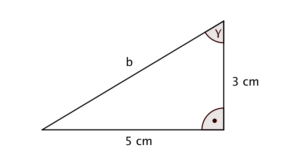
- Bestimme die Größe des Winkels.
- Bestimme die Länger der Seite.
Lösungen:
- Dieser Aufgabenteil lässt sich dem Themengebiet Trigonometrie zuordnen. Vom Winkel $y$ aus betrachtet, handelt es sich bei der $5??$ langen Seite um die Gegenkathete und bei der $3??$ langen Seite um die Ankathete. Es gilt die folgende Winkelbeziehung:
\begin{align*} \tan \gamma = \dfrac{\text{Gegenkathete}}{\text{Ankathete}} = \dfrac{5}{3} \Rightarrow \gamma = \tan^{(−1)} \dfrac{5}{3} \approx 59^o\end{align*}. - Die fehlende Seitenlänge (Hypotenuse) kann mit dem Satz des Pythagoras berechnet werden: \begin{align*} 5^2+3^2=b^2 \Leftrightarrow 25+9=b^2 \Leftrightarrow 34=b^2 \Rightarrow 5{,}8 \approx b \end{align*}.
Schau dir zur Vertiefung Daniels Playlist zum Thema Flächen und Umfang an!