
Bruchrechnung
Das Thema Bruchrechnung begleitet uns unser ganzes Leben. Umso wichtiger ist es, dass die Grundlagen der Bruchrechnung schnell und einfach verstanden werden. Hierfür haben wir euch alle wichtigen Themen rund um die Bruchrechnung zusammengefasst.
Was dich auf dieser Seite erwartet:
- Bruchrechnung Grundlagen
- Bruchrechnung einfaches Beispiel
- Bruchrechnung Regeln
- Unechter Bruch
- Beispielaufgabe Bruchrechnung
Bruchrechnung Grundlagen
Brüche und Dezimalzahlen sind Schreibweisen, um Zahlen zu beschreiben, die Einstieg zwischen den natürlichen Zahlen (also 1, 2, 3, 4, 5 . . . ) liegen. Auf diese Weise können wir z.B. eine Hälfte oder ein Viertel ausdrücken. Der Zähler (oben) gibt an, wie viele Teile davon genommen werden. Beispiel: $\frac{4\ }{5\ }\ \frac{(Zähler)}{(Nenner)}$
Bruchrechnung einfaches Beispiel
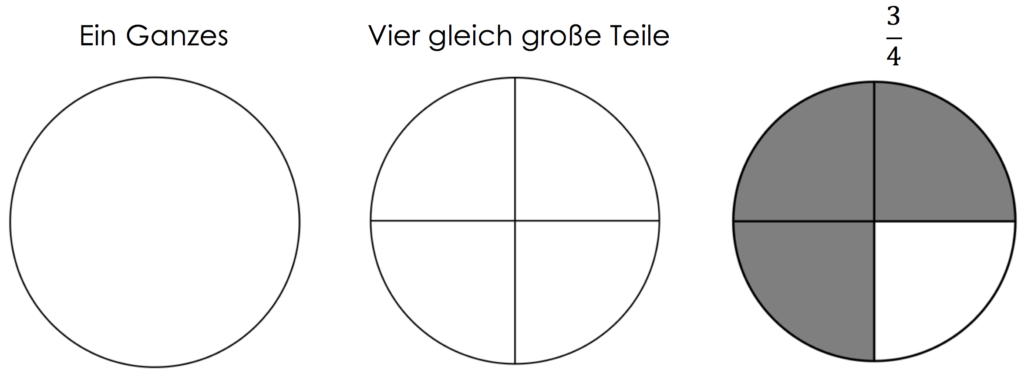
Stellen wir uns vor, dass wir eine Tafel Schokolade gleichmäßig auf vier Personen aufteilen möchten. Hierfür müssen wir die Tafel in vier gleich große Stücke unterteilen. Die Gesamtmenge der Stücke ist in unserem Bruch der Nenner. Die Anzahl an Stücken, die jede Person von der Gesamtmenge bekommt, ist der Zähler. Damit beträgt in unserem Beispiel der Nenner vier und der Zähler eins. Jede Person erhält also $\frac{1}{4}$ der Schokolade. Wenn jetzt eine Person kein Stück möchte und du dafür ihr Viertel bekommst, hast du $\frac{2}{4}$. Da du zwei Stücke von der Gesamtmenge erhältst, beträgt der Zähler nun zwei.
- In wie viele Teile unterteilen wir die Schokolade? $\rightarrow \textbf{Nenner}$
- Wie viele Teile davon bekommt eine Person? $\rightarrow \textbf{Zähler}$
Wenn wir das verstanden haben, können wir Zahlen beliebig fein unterteilen. Je größer der Nenner dabei ist, desto feiner die Unterteilung (wir haben dann ja viel mehr Teile).
Wenn die Anzahl der Stücke (Zähler) mit der Gesamtmenge an Stücken (Nenner) übereinstimmt, sprechen wir von einem Ganzen. Im Bruch können wir ein Ganzes z.B. als $\frac{1}{1}$, $\frac{2}{2}$ oder $\frac{8}{8}$ ausdrücken. Wenn also Zähler und Nenner gleich groß sind, haben wir immer ein Ganzes. Wir können aber auch Zahlen darstellen, die größer sind als eins, z.B. $\frac{3}{2}$ oder $\frac{8}{4}$.
Schau dir zur Vertiefung das Video zur Bruchrechnung von Daniel an!
Bruchrechnung Regeln
Brüche erweitern
Ein Bruch wird erweitert, indem man sowohl den Zähler (oben) als auch den Nenner (unten) des Bruchs mit der gleichen Zahl multipliziert. Die Zahl über dem Pfeil gibt an, dass der Bruch mit 2 erweitert wird:
\[\frac{\mathrm{3}}{\mathrm{7}}\ \ \ {{\stackrel{\mathrm{2}}{\longrightarrow}}}\ \ \ \frac{\mathrm{3}\mathrm{\cdot }\mathrm{2}}{\mathrm{7}\mathrm{\cdot }\mathrm{2}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{6}}{\mathrm{14}}\]
Brüche kürzen
Ein Bruch wird gekürzt, indem man sowohl den Zähler (oben) als auch den Nenner (unten) durch die gleiche Zahl teilt. Die Zahl unter dem Pfeil gibt an, dass der Bruch mit 9 gekürzt wird:
\[\frac{\mathrm{9}}{\mathrm{27}}\ \ \ {{\mathop{\longrightarrow}\limits_{\mathrm{9}}}}\ \ \ \frac{\mathrm{9\div 9}}{\mathrm{27\div 9}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{1}}{\mathrm{3}}\]
Brüche addieren
Stellen wir uns einmal vor, dass wir gerade zu Hause eine Pizza essen. Wir haben das erste Viertel gegessen und haben dementsprechend drei Viertel der Pizza noch übrig. Oder wir könnten sagen, dass wir eine halbe Pizza und noch ein Viertel haben, denn zwei Viertel sind ja das Gleiche wie eine halbe Pizza. Wenn wir das mathematisch ausdrücken, heißt das:
\begin{align*}
\frac{1}{2} + \frac{1}{4} = \frac{3}{4}
\end{align*}
An dieser kleinen Aufgabe sehen wir schon das einzig Schwierige am Bruchrechnen: Der Nenner. Wir erinnern uns: Der Nenner war die Zahl, durch die wir die Pizza teilen. Um Brüche miteinander verrechnen zu dürfen, müssen wir immer beide Nenner auf die gleiche Zahl bringen. In unserem Beispiel würde das heißen: Wir sagen, unser $\frac{1}{2}$ Stück Pizza ist das Gleiche wie $\frac{2}{4}$ Stücke Pizza. Dann würde unsere Gleichung so aussehen:
\begin{align*}
\frac{2}{4} + \frac{1}{4} = \frac{3}{4}
\end{align*}
Wir sehen, dass der Nenner die ganze Zeit gleich bleibt und der Zähler einfach addiert wird. Also: $2 + 1 = 3$ und der Nenner bleibt die ganze Zeit 4.
Brüche subtrahieren
Beim Subtrahieren machen wir genau das Gleiche, nur eben, dass wir $\frac{1}{4}$ von $\frac{2}{4}$ abziehen. Das sieht anschließend wie folgt aus:
\begin{align*}
\frac{2}{4} – \frac{1}{4} = \frac{1}{4}
\end{align*}
Logisch oder? Wenn wir von unserer halben Pizza noch ein Viertel essen, haben wir noch ein Viertel übrig. Das Verrechnen ist also relativ einfach. Schau dir das nächste Teilkapitel genau an. Denn das Schwierige ist, den Nenner richtig zu kürzen oder zu erweitern.
Brüche multiplizieren
Zwei Brüche werden multipliziert, indem wir „Zähler mit Zähler“ und „Nenner mit Nenner“ multiplizieren:
\[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{\cdot }\frac{\mathrm{3}}{\mathrm{4}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{1}\mathrm{\cdot }\mathrm{3}}{\mathrm{2}\mathrm{\cdot }\mathrm{4}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{3}}{\mathrm{8}}\]
Die Brüche sollten, falls möglich, vor der Multiplikation über Kreuz gekürzt werden:
\begin{align*}
\frac{3}{7} \cdot \frac{14}{27} \ \ \ = \ \ \ \frac{1}{1} \cdot \frac{2}{9}\ \ \ = \ \ \ \frac{2}{9}
\end{align*}
Unechter Bruch
Eine gemischte Zahl (Ganze Zahl und Bruch z.B. $\mathrm{2}\frac{\mathrm{1}}{\mathrm{4}}$) kann nach folgendem Schema in einen unechten Bruch (Zähler > Nenner) umgewandelt werden:
\[\mathrm{2}\frac{\mathrm{1}}{\mathrm{4}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{2}\mathrm{\cdot }\mathrm{4+1}}{\mathrm{4}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{9}}{\mathrm{4}}\]
Brüche dividieren
Zwei Brüche werden dividiert, indem man bei dem Bruch, durch den geteilt wird, den Zähler und den Nenner vertauscht (Kehrwert bildet) und danach die beiden Brüche miteinander multipliziert:
\[\frac{\mathrm{3}}{\mathrm{7}}\mathrm{\div }\frac{\mathrm{27}}{\mathrm{14}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{3}}{\mathrm{7}}\mathrm{\cdot }\frac{\mathrm{14}}{\mathrm{27}}\ \ \ \mathrm{=}\ \ \ \frac{\mathrm{2}}{\mathrm{9}}\]
Bitte das Ergebnis bei allen Grundrechenarten immer vollständig kürzen!
NEU
Beispielaufgabe Bruchrechnung
Ordne die folgenden Zahlen nach ihrer Größe. Beginne mit der kleinsten Zahl:
\begin{align*}
0,25; \frac{1}{5}; -0,3 ; 0,225; -\frac{1}{3}
\end{align*}
Lösung Bruchrechnung:
Bevor wir unsere Zahlen der Größe nach ordnen können, empfiehlt es sich, diese in Dezimalzahlen umzuwandeln:
\begin{align*}
\frac{1}{5} = 0,2
\end{align*}
\begin{align*}
-\frac{1}{3} = -0,\overline{3}
\end{align*}
Jetzt können wir unsere Zahlen der Größe nach aufsteigend ordnen:
\begin{align*}
-0,\overline{3} < -0,3 < 0,2 < 0,225 < 0,25
\end{align*}
Weitere Erklärungen inkl. Aufgaben zum Thema Brüche rechnen gibt es im passenden Lernvideo:
NEU
