Folgen und Grenzwerte

In diesem Kapitel beschäftigen wir uns mit den sogenannten $\textbf{Folgen}$ und der $\textbf{Konvergenz von Folgen}$. Dazu starten wir mit einem definierenden Beispiel. Betrachten wir diese Aufzählung von Zahlen:

\begin{align*}
1,~ 3,~ 7,~ 15,~ 31,~ 63,~ ?
\end{align*}

Was wir unter einer Folge verstehen, ist vergleichbar mit Themen bzw. Aufgabenstellungen eines IQ-Tests. Mathematisch gesehen ist es eine Abbildung von den natürlichen Zahlen in einem Zielraum, der meist den reellen Zahlen entspricht. Dies schreiben wir kurz durch:

\begin{align*}
a_n:=a(n):\mathbb{N}\rightarrow\mathbb{R}
\end{align*}

Dabei wird jede einzelne Ausprägung Folgeglied genannt, während die gesamte Abbildung als Folge zu verstehen ist. In unserem Beispiel gilt also:

\begin{align*}
a_1 &= 1\\
a_2 &= 3\\
a_3 &= 7\\
& \text{usw.}
\end{align*}

Wir zählen die einzelnen Elemente ab und geben ihnen eine Bezeichnung.

Die Fragestellung lässt sich nun dahingehend übersetzen, dass wir wissen möchten, welchen Wert das Folgeglied $a_7$ hat.

Zwei existierenden Darstellungsformen von Folgen:

1. explizite Darstellung
2. rekursive Darstellung

Was das bedeutet, werden wir sofort am Beispiel verdeutlichen. Schauen wir uns einmal an, wie wir von einer Zahl zu ihrem Nachfolger gelangen:

\begin{align*}
\underbrace{1,~ 3}_{\cdot 2 + 1},~ 7,~ 15,~ 31,~ 63,~ ?\\
1,~ \underbrace{3,~ 7}_{\cdot 2 + 1},~ 15,~ 31,~ 63,~ ?\\
1,~ 3,~ \underbrace{7,~ 15}_{\cdot 2 + 1},~ 31,~ 63,~ ?\\
1,~ 3,~ 7,~ \underbrace{15,~ 31}_{\cdot 2 + 1},~ 63,~ ?\\
1,~ 3,~ 7,~ 15,~ \underbrace{31,~ 63}_{\cdot 2 + 1},~ ?\\
1,~ 3,~ 7,~ 15,~ 31,~ \underbrace{63,~ ?}_{\cdot 2 + 1}
\end{align*}

Hier erkennen wir schnell, dass sich die Formel, um von einer Zahl zur nächsten zu gelangen, nicht ändert. Wir nehmen immer den Wert des aktuellen Folgeglieds, für z.B. $7$, multiplizieren mit $2$ und addieren $1$ und erhalten mit $2\cdot7+1=15$ den Nachfolger. Bei dieser Methode haben wir, ohne es zu wissen, die rekursive Beziehung der Folge erkannt. Denn mathematisch lässt sich dies wie folgt festhalten:

\begin{align*}
a_1 &= 1 \\
a_n&=2\cdot a_{n-1}+1
\end{align*}

Damit lässt sich auch $a_7$ errechnen, denn es gilt $a_7=2\cdot \overbrace{63}^{=a_6} + 1=127$. So können wir auch direkt die charakteristischen Eigenschaften von rekursiv definierten Folgen festhalten.

Merke:

1. Bei einer rekursiv definierten Folge benötigen wir stets einen oder mehrere Startpunkte (hier: $a_1=1$).
2. Bei rekursiv definierten Folgen lässt sich das $n$-te Folgeglied immer mit Hilfe eines oder mehrerer Vorgänger errechnen (hier: $a_n = 2\cdot a_{n-1}+1$).

Wenn bei der Vorschrift der Rekursion mehrere Vorgänger benötigt werden, werden ebenso mehrere Startwerte gebraucht. Ein sehr bekanntes Beispiel für einen solchen Sachverhalt liefert die Fibonacci-Folge. Diese ist durch

\begin{align*}
a_0&=1 \\
a_1 &= 1\\
a_{n+1}&=a_n+a_{n-1}
\end{align*}

definiert. Wir sehen hier, dass wir für die Berechnung des $n+1$-ten Folgeglieds sowohl das $n$-te als auch das $n-1$-te Folgeglied benötigen. Dementsprechend brauchen wir für eine wohldefinierte Folge auch zwei Startwerte.

Der Vorteil dieser Art der Definition ist, dass sich die rekursive Beziehung meist leichter erkennen lässt. Der Nachteil hingegen liegt darin, dass wir in der Regel alle bisherigen Folgeglieder berechnen müssen, um zukünftige zu erhalten.

Beispiel:
Berechne für die Folge aus diesem Beispiel den Wert von $a_{1234}$. Ziemlich umständlich und zeitraubend, wenn wir sie über die Rekursion lösen möchten. Hier kommt nun die zweite Möglichkeit zum Einsatz: die sogenannte $\textbf{explizite Darstellung}$. Das Erkennen ist bei dieser Methode etwas schwieriger. Da wir in der Rekursion bereits gesehen haben, dass wir den Vorgänger immer mit $2$ multiplizieren müssen, betrachten wir mal die Zweierpotenzen:

\begin{align*}
2^0 = 1,~2^1 = 2,~2^2 = 4,~2^3 = 8,~2^4 = 16,~2^5 = 32
\end{align*}

Es wird ersichtlich, dass die Zahlen aus dem Beispiel immer um $1$ niedriger sind, als die Potenzen. Daher erschließen wir, dass

\begin{align*}
a_n = 2^{n}-1
\end{align*}

gilt. Zur Kontrolle rechnen wir noch schnell zwei Werte nach:

\begin{align*}
a_5 &= 2^5 -1 = 32-1=31 \quad \checkmark\\
a_7 &= 2^7-1 = 128 – 1 = 127 \quad \checkmark
\end{align*}

Merke

1. Der Vorteil der expliziten Darstellung ist, dass wir keinen Startpunkt benötigen und jedes Folgeglied ohne jegliche Berechnung der Vorgänger bestimmen können.

Beispielsweise ist $a_{15} = 2^{15} – 1 = 32768 -1 =32767$. Der Nachteil gegenüber der rekursiven Beziehung besteht hier in der Schwierigkeit, diese Darstellung zu erkennen.

Abschließend können wir noch zeigen, dass unsere beiden Darstellungen der Folge auch zusammenpassen. Dafür setzen wir die Formel der einen in die andere ein und es ergibt sich mit

\begin{align*}
a_n = \underbrace{2\cdot a_{n-1} + 1}_{rekursiv} = 2\cdot (\underbrace{2^{n-1}-1}_{explizit})+1 = 2^n-2+1 = 2^n-1
\end{align*}

eine wahre Aussage.

Eigenschaften von Folgen

Die erste Eigenschaft, die wir betrachten, ist die $\textbf{Monotonie}$. Allgemein können wir die Formel zur Monotonie technisch schnell in einer Tabelle darstellen:

\begin{array}{c|c}
a_n \text{ist monoton wachsend} & a_n \text{ist monoton fallend} \\
\hline
\frac{a_{n+1}}{a_n}\geq 1 & \frac{a_{n+1}}{a_n}\leq 1 \\
a_{n+1}-a_n\geq 0$ & $a_{n+1}-a_n\leq 0
\end{array}

Dazu sei angemerkt, dass wir von strenger Monotonie, also streng monoton wachsend und streng monoton fallend sprechen, wenn statt der Zeichen $\leq$ und $\geq$ in obiger Tabelle, jeweils die Zeichen $<$ und $>$ stehen.

Wir betrachten erneut unser $\textbf{Beispiel}$ $a_n=2^n-1$. Welche der beiden Formeln wir benutzen, ist einerseits Geschmackssache, andererseits hängt es aber auch etwas von der Folge ab, die betrachtet werden soll. Oftmals ist sowohl der Quotient als auch die Differenzbildung möglich und zielführend. In unserem Fall sieht der Quotient von Summen zunächst weniger schön aus, sodass wir uns für die zweite Zeile entscheiden. Wir beginnen daher mit der linken Seite und schauen, ob wir diese $\geq 0$ oder $\leq 0$ zeigen können. Es gilt:

\begin{align*}
a_{n+1}-a_n = 2^{n+1}-1-(2^n-1) = 2\cdot 2^n-1-2^n+1 = 2^n>0.
\end{align*}

Wir sehen, dass unsere Folge streng monoton wachsend ist. Oftmals, mathematisch gesehen erst zu 100\ korrekt, ist es von Vorteil die Monotonie mit der vollständigen Induktion zu zeigen.

\par

Eine weitere mögliche Eigenschaft einer Folge ist die $\textbf{Beschränktheit}$. Diese sagt etwas darüber aus, ob sich die Folge stets oberhalb bzw. unterhalb eines Wertes oder, wenn dies beides erfüllt ist, zwischen zwei Werten befindet. Das Erkennen einer solchen Schranke ist nicht immer leicht. Hier ist es ratsam ein paar Folgeglieder zu betrachten oder mittels Taschenrechner zu berechnen und eine Vermutung aufzustellen. Auch ein genauer Blick auf die Definition der Folge kann hier helfen. Anschließend kann diese Vermutung per Induktion bewiesen werden. In unserem Beispiel $a_n=2^n-1$ sehen wir schnell, dass diese Folge nach oben nicht beschränkt sein kann, da $\lim\limits_{ n\rightarrow\infty}2^n = \infty$ gilt. Daran ändert auch die $-1$ nichts. Für eine untere Schranke gibt es mehrere Möglichkeiten, da diese nicht eindeutig ist. Es kann hier schnell auf die Zahl $0$ als untere Schranke raus kommen. Da wir natürliche Zahlen aber so verstehen, dass diese bei $1$ beginnen, können wir auch $1$ als untere Schranke zeigen.

1. $\textbf{Induktionsanfang}$ $n=1$: $a_1 = 2^1-1 = 1 \geq 1 \quad \checkmark$
2. $\textbf{Induktionsvoraussetzung:}$ Die Behauptung $a_n\geq 1$ gelte für ein $n\in\mathbb{N}$ beliebig.
3. $\textbf{Induktionsschritt}$ $n \rightarrow n+1$: $a_{n+1}=2^{n+1}-1\geq 2^n-1 = a_n~\overset{\text{I.V.}}{\geq}~1$

Konvergenz

Eine sehr wichtige Eigenschaft ist die $\textbf{Konvergenz von Folgen}$. Diese ist erfahrungsgemäß nicht leicht zu verstehen, daher werden wir uns langsam an die Sache herantasten. Zunächst ist zu klären, was wir unter der Konvergenz von Folgen genau verstehen. Ein salopper Definitionsversuch wäre zu sagen, dass eine Folge $a_n$ gegen einen Grenzwert $a$ konvergiert, wenn sie sich diesem im Unendlichen immer weiter annähert. Die Definition halten wir nun mathematisch fest, um Interpretationsspielräume auszuschließen.

Definition Konvergenz
Sei $a_n:\mathbb{N}\rightarrow\mathbb{R}$ eine Folge und $a\in\mathbb{R}$, so sagen wir, dass $a_n$ gegen $a$ konvergiert, in Zeichen $\lim\limits_{n\rightarrow\infty}a_n = a$, wenn
\begin{align*}
\forall~\varepsilon>0~\exists~n_0\in\mathbb{N}:\forall~n\geq n_0:~
\left|a_n-a\right|<\varepsilon. \end{align*} Dies bedeutet, dass egal welchen Wert für $\varepsilon$ wir uns vorgeben, wir immer einen Index $n_0$ finden, der in der Regel von $\varepsilon$ abhängt, sodass alle Folgeglieder mit einem höheren Index einen kleineren Abstand zum Grenzwert $a$ haben als $\varepsilon$. Zudem halten wir fest, dass eine Folge, die nicht konvergiert, $\textbf{divergent}$ genannt wird und wir eine Folge, die gegen $0$ konvergiert, $\textbf{Nullfolge}$ nennen. Betrachten wir die Folge $a_n=1+\frac{1}{n}$.

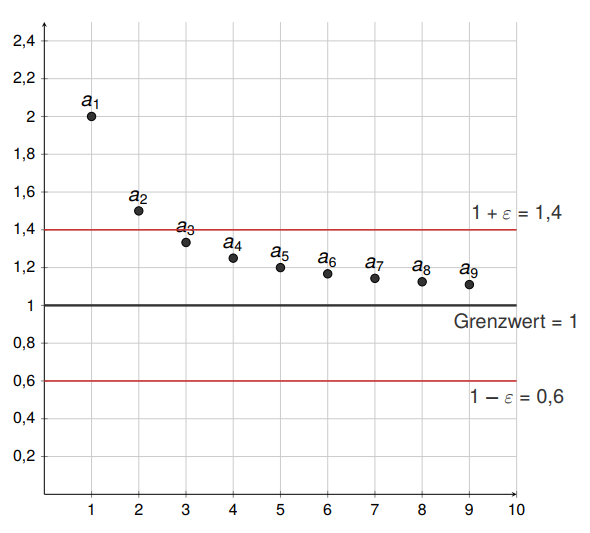
und geben erhalten wir für den Grenzwert $1$ dieser Folge einen $\varepsilon-$Schlauch\grqq{} mit $1+0{,}4 = 1{,}4$ und $1-0{,}4=0{,}6$. Die Definition der Konvergenz sagt jetzt aus, dass egal wie klein wir das $\varepsilon$ wählen, es immer einen Index gibt, ab welchem alle weiteren Elemente der Folge innerhalb dieses Schlauchs landen und auch nicht mehr verlassen! In obiger Zeichnung für $\varepsilon=0{,}4$ ist dies bereits ab $a_3$ erfüllt. Würden wir $\varepsilon$ verkleinern und beispielsweise $\varepsilon=0{,}2$ betrachten, so wären die Folgeglieder erst ab $a_6$ und allen weiteren Elementen innerhalb des Schlauchs. Wir werden mathematisch zeigen, dass der in der Zeichnung behauptete Grenzwert korrekt ist, also dass gilt: $a=1$. Dazu müssen wir obige Definition nachrechnen. Zunächst betrachten wir die Differenz:

\begin{align*}
\left|a_n-1\right| = \left|1+\frac{1}{n}-1\right| = \left|\frac{1}{n}\right|=\frac{1}{n}
\end{align*}

Nun fordern wir, dass $n_0\geq\frac{1}{\varepsilon}$ ist, welches für jedes $\varepsilon>0$ gefunden werden kann. Damit gilt dann für alle $n>n_0$:

\begin{align*}
\frac{1}{n}<\frac{1}{n_0}=\frac{1}{\frac{1}{\varepsilon}}=\varepsilon \end{align*} Insgesamt haben wir nach der Definition der Konvergenz von Folgen also gezeigt, dass $\lim\limits_{n\rightarrow\infty}a_n=1$ gilt. Der große Nachteil bei direktem Nachrechnen der Definition ist, dass der Grenzwert $a$, in diesem Falle $1$, bekannt sein oder zumindest richtig geraten werden muss, um anschließend verifiziert werden zu können. Daher werden wir im Folgenden verschiedene Hilfsmittel besprechen, um die Konvergenz auch mit anderen Methoden zeigen zu können. Als Erstes betrachten wir verschiedene $\textbf{Grenzwertsätze}$. Diese erlauben es, zusammengesetzte Folgen in ihren Einzelheiten zu untersuchen und die Grenzwerte anschließend zusammenzufassen. Beipsiel
Gegeben seien die Folgen $(a_n)_{n\in\mathbb{N}}$ und $(b_n)_{n\in\mathbb{N}}$ mit $\lim\limits_{n\rightarrow\infty}a_n=a$ und $\lim\limits_{n\rightarrow\infty}b_n=b$. Dann gilt:

1. $\lim\limits_{n\rightarrow\infty}|a_n|=|a|$
2. $\lim\limits_{n\rightarrow\infty}a_n+b_n=a+b$
3. $\lim\limits_{n\rightarrow\infty}c\cdot a_n=c\cdot a$ für alle $c\in\mathbb{R}$
4. $\lim\limits_{n\rightarrow\infty}a_n\cdot b_n=a\cdot b$
5. $\lim\limits_{n\rightarrow\infty}a_n^k=a^k$ für $k\in\mathbb{N}$

Gilt $b_n\neq 0$ und $b\neq 0$, dann folgt:
$\lim\limits_{n\rightarrow\infty}\frac{a_n}{b_n}=\frac{a}{b}$

Gilt $a_n\geq 0$, dann folgt:
$\lim\limits_{n\rightarrow\infty}\sqrt[k]{a_n}=\sqrt[k]{a}$

Um diese \qrcodesidestart\qrcodeside{https://stdy.help/r/bcc93d43c7}{Grenzwertsätze}Grenzwertsätze gewinnbringend anwenden zu können, bedarf es einiger bekannter Grenzwerte von Folgen.

1. $\lim\limits_{n\rightarrow\infty}a=a$, für $a\in\mathbb{R}$
2. $\lim\limits_{n\rightarrow\infty}\frac{1}{n^k}=0$, für $k>0$
3. $\lim\limits_{n\rightarrow\infty}\frac{n^k}{c^n}=0$, für $k,~c>0$
4. $\lim\limits_{n\rightarrow\infty}\sqrt[n]{c}=1$, für $c>0$
5. $\lim\limits_{n\rightarrow\infty}\sqrt[n]{n}=1$
6. $\lim\limits_{n\rightarrow\infty}q^n=0$, für $|q|<1$
7. $\lim\limits_{n\rightarrow\infty}q^n=\infty$, für $|q|>1$

Die Folge $q^n$, welche in den Punkten $6.$ und $7.$ beschrieben wird, heißt $\textbf{geometrische Folge}$ und wird im Kapitel über Summen und Reihen ebenfalls eine Rolle spielen. Mit Hilfe der Grenzwertsätze und dieser ersten bekannten Grenzwerte sind wir in der Lage, Folgen zu bearbeiten, die aus diesen Arten zusammengesetzt sind. Daher werden wir einige Beispiele dazu betrachten. Hierbei darf nicht vergessen werden, dass wir uns bei Folgen in den natürlichen Zahlen bewegen und eventuelle Grenzwertmethoden aus dem Kapitel der Funktionen nicht direkt anwendbar sind.

Beispiel: Wir betrachten einen Bruch aus zwei Polynomen.

1. Finde den Summanden im Nenner, der am schnellsten wächst und die anderen dominiert.
2. Klammere sowohl im Zähler als auch im Nenner diese Potenz aus, auch wenn sie größer als die Potenzen ist, die im Zähler vorkommen.
3. Kürze die größte Potenz.
4. Benutze bei Konvergenz die Grenzwertsätze $2.$ und $6.$.
5. Sollte im Zähler ein divergenter Teil vorkommen, so argumentieren wir anders. Dies ist der Fall, falls die größte Potenz des Zählers größer ist, als die größte Potenz des Nenners.

Der Summand, der im Nenner am stärksten wächst, ist $n^2$, sodass wir diesen ausklammern und kürzen.

\begin{align*}
=\lim\limits_{n\rightarrow\infty}\frac{n^2\cdot(3-\frac{4n}{n^2}+\frac{5}{n^2})}{n^2\cdot(\frac{6}{n^2}-5+\frac{9n}{n^2})}=\lim\limits_{n\rightarrow\infty}\frac{3-\frac{4}{n}+\frac{5}{n^2}}{\frac{6}{n^2}-5+\frac{9}{n}}
\end{align*}

Mit Hilfe der Grenzwertsätze können wir nun die Grenzwerte der einzelnen Summanden im Zähler und im Nenner bestimmen:

\begin{align*}
&=\frac{\overbrace{\lim\limits_{n\rightarrow\infty}3}^{\rightarrow~3}-\overbrace{\lim\limits_{n\rightarrow\infty}\frac{4}{n}}^{\rightarrow~0}+\overbrace{\lim\limits_{n\rightarrow\infty}\frac{5}{n^2}}^{\rightarrow~0}}{\underbrace{\lim\limits_{n\rightarrow\infty}\frac{6}{n^2}}_{\rightarrow~ 0}-\underbrace{\lim\limits_{n\rightarrow\infty}5}_{\rightarrow~ 5}+\underbrace{\lim\limits_{n\rightarrow\infty}\frac{9}{n}}_{\rightarrow~0}} =\frac{3-0+0}{0-5+0} = -\frac{3}{5}
\end{align*}

Beispiel: Wir betrachten folgenden Ausdruck: $\lim\limits_{n\rightarrow\infty}\frac{3n^5-3^{n+1}+2}{2^{2n}+n^2+3^n}$
Zunächst müssen wir den Summanden, der im Nenner am stärksten wächst, finden. Dies ist in diesem Falle nicht $3^n$, da wir zunächst $2^{2n}=4^n$ umschreiben und mit $4$ die größere Basis haben. Also klammern wir nun $4^n$ im Zähler und Nenner aus und kürzen:

\begin{align*}
=\lim\limits_{n\rightarrow\infty}\frac{3n^5-3\cdot 3^{n}+2}{4^{n}+n^2+3^n} &= \lim\limits_{n\rightarrow\infty}\frac{4^n\cdot(\frac{3n^5}{4^n}-3\cdot\frac{3^{n}}{4^n}+\frac{2}{4^n})}{4^n\cdot(1+\frac{n^2}{4^n}+\frac{3^n}{4^n})} =\lim\limits_{n\rightarrow\infty}\frac{\frac{3n^5}{4^n}-3\cdot\left(\frac{3}{4}\right)^n+\frac{2}{4^n}}{1+\frac{n^2}{4^n}+\left(\frac{3}{4}\right)^n}
\end{align*}

Anschließend benutzen wir erneut die Grenzwertsätze und erhalten das Ergebnis anhand der bekannten Grenzwerte aus der vorherigen Tabelle:

\begin{align*}
=\frac{\overbrace{\lim\limits_{n\rightarrow\infty}\frac{3n^5}{4^n}}^{\rightarrow~0}-\overbrace{\lim\limits_{n\rightarrow\infty}3\cdot\left(\frac{3}{4}\right)^n}^{\rightarrow~0}+\overbrace{\frac{2}{4^n}}^{\rightarrow~0}}{\underbrace{\lim\limits_{n\rightarrow\infty}1}_{\rightarrow~1}+\underbrace{\lim\limits_{n\rightarrow\infty}\frac{n^2}{4^n}}_{\rightarrow_0}+\underbrace{\lim\limits_{n\rightarrow\infty}\left(\frac{3}{4}\right)^n}_{\rightarrow~0}} = \frac{0+0+0}{1+0+0} =0
\end{align*}

Beispiel: Wir betrachten folgenden Ausdruck: $\lim\limits_{n\rightarrow\infty}\frac{2^n+(-1)^n+4}{n^{10}-\sqrt[n]{n}-1}$
Auch in diesem Fall klammern wir zunächst den am stärksten wachsenden Exponenten im Nenner aus (hier: $n^{10}$) und kürzen anschließend

\begin{align*}
=\lim\limits_{n\rightarrow\infty}\frac{n^{10}\cdot(\frac{2^n}{n^{10}}+\frac{(-1)^n}{n^{10}}+\frac{4}{n^{10}})}{n^{10}\cdot(1-\frac{\sqrt[n]{n}}{n^{10}}-\frac{1}{n^{10}})}=\lim\limits_{n\rightarrow\infty}\frac{\frac{2^n}{n^{10}}+\frac{(-1)^n}{n^{10}}+\frac{4}{n^{10}}}{1-\frac{\sqrt[n]{n}}{n^{10}}-\frac{1}{n^{10}}}.
\end{align*}

An dieser Stelle können wir keinen Gebrauch von den Grenzwertsätzen machen, da $\frac{2^n}{n^{10}}$ divergiert und die Grenzwertsätze nur bei konvergenten Folgen angewandt werden dürfen. Zur Lösung dieses Beispiels betrachten wir daher die beiden Folgen $\frac{2^n}{n^{10}}+\frac{(-1)^n}{n^{10}}+\frac{4}{n^{10}}$ und $1-\frac{\sqrt[n]{n}}{n^{10}}-\frac{1}{n^{10}}$ getrennt. Die erste divergiert gegen $\infty$, da der erste Summand gegen $\infty$ divergiert und die anderen beiden Folgen Nullfolgen sind. Die Folge im Nenner konvergiert gegen $1$, da der erste Summand gegen $1$ konvergiert und die anderen Summanden Nullfolgen sind. Das bedeutet, wir haben einen beschränkten Nenner und einen unbeschränkten Zähler, sodass die Folge insgesamt unbeschränkt ist und damit gilt

\begin{align*}
\lim\limits_{n\rightarrow\infty}\frac{2^n+(-1)^n+4}{n^{10}-\sqrt[n]{n}-1} = \infty
\end{align*}

Ein argumentatives Vorgehen ist nach dem Kürzen immer dann nötig, wenn der am stärksten wachsende Summand im Zähler den am stärksten wachsenden Summanden im Nenner dominiert.

Auch dieses Vorgehen verstehen wir anhand von Beispielen besser. \newline \textbf{Beispiel} Betrachten wir im Folgenden den Grenzwert

\begin{align*}
\lim\limits_{n\rightarrow\infty}\sqrt[n]{2^n+3^n+4^n}.
\end{align*}

An dieser Stelle dürfen wir nicht die Wurzel aus den einzelnen Summanden ziehen. Aber wir finden zwei Folgen, die diese Folge von oben und unten wie ein Sandwich einschließen und uns bei der Lösungsfindung helfen. Zum Einen ist

\begin{align*}
2^n+3^n+4^n \geq 4^n,
\end{align*}

da alle Summanden positiv sind. Auf der anderen Seite gilt aber auch

\begin{align*}
2^n+3^n+4^n\leq 4^n+4^n+4^n = 3\cdot 4^n.
\end{align*}

Mit diesen Abschätzungen erhalten wir nun die Grenzwerte

\begin{align*}
\lim\limits_{ n\rightarrow\infty}\sqrt[n]{4^n} =\lim\limits_{ n\rightarrow\infty} 4 = 4 \qquad \qquad
\lim\limits_{ n\rightarrow\infty}\sqrt[n]{3\cdot 4^n} =4\cdot\underbrace{\lim\limits_{ n\rightarrow\infty}\sqrt[n]{3}}_{\rightarrow~1}=4
\end{align*}

und damit haben wir mit dem Sandwich-Lemma das Ergebnis

\begin{align*}
4 = \lim\limits_{ n\rightarrow\infty}\sqrt[n]{4^n}\leq \lim\limits_{ n\rightarrow\infty}\sqrt[n]{2^n+3^n+4^n}\leq \lim\limits_{ n\rightarrow\infty}\sqrt[n]{3\cdot 4^n}=4,
\end{align*}

sodass $\lim\limits_{ n\rightarrow\infty}\sqrt[n]{2^n+3^n+4^n}=4$ gilt.

Im Anschluss möchten wir eine weitere Klasse von Folgen betrachten, welche mit einem kleinen Trick schnell gelöst werden kann. Dabei handelt es sich um die \textbf{Differenz zweier Wurzeln}. Betrachten wir als \textbf{Beispiel} die Folge $(a_n)_{n\in\mathbb{N}}$ mit $a_n=\sqrt{n}-\sqrt{n-1}$. An dieser Stelle nutzen wir die 3. binomische Formel und erweitern mit der Summe der beiden Wurzeln. Wir erhalten:

\begin{align*}
\lim\limits_{ n\rightarrow\infty}\sqrt{n}-\sqrt{n-1}&=\lim\limits_{ n\rightarrow\infty}\frac{(\sqrt{n}-\sqrt{n-1})\cdot(\sqrt{n}+\sqrt{n-1})}{\sqrt{n}+\sqrt{n-1}}\\
&=\lim\limits_{ n\rightarrow\infty}\frac{\sqrt{n}^2-\sqrt{n-1}^2}{\sqrt{n}+\sqrt{n-1}} =\lim\limits_{ n\rightarrow\infty}\frac{n-(n-1)}{\sqrt{n}+\sqrt{n-1}} =\lim\limits_{ n\rightarrow\infty}\frac{1}{\sqrt{n}+\sqrt{n-1}}
\end{align*}

Mit Hilfe des oben eingeführten Sandwich-Lemmas zeigen wir die Konvergenz dieser Folge gegen $0$ mit den beiden Abschätzungen:

\begin{align*}
\sqrt{n}+\sqrt{n-1}&\geq\sqrt{n}\\
\sqrt{n}+\sqrt{n-1}&\leq\sqrt{n}+\sqrt{n}=2\cdot\sqrt{n}
\end{align*}

Mit $0=\lim\limits_{ n\rightarrow\infty}\frac{1}{2\cdot\sqrt{n}}\leq\lim\limits_{ n\rightarrow\infty}\frac{1}{\sqrt{n}+\sqrt{n-1}}\leq\lim\limits_{ n\rightarrow\infty}\frac{1}{\sqrt{n}}=0$
folgt die Behauptung.

$\textbf{Anmerkung}$: Bei einer Nullfolge ist es genauso korrekt, als untere Abschätzung die konstante Folge $0$ statt $\frac{1}{2\cdot\sqrt{n}}$ zu wählen.