
Der erste Hauptsatz der Thermodynamik
In diesem Artikel lernst du alle Grundlagen zum ersten Hauptsatz der Thermodynamik. Wichtig: Schaue dir zuerst als Einführung das Lernvideo an, damit du danach das Kapitel durcharbeiten kannst.
Wir haben die einzelnen Energieformen sowie die Prozessgrößen Wärme und Arbeit betrachtet. Im ersten Hauptsatz der Thermodynamik werden all diese Größen in einer Systembilanz zusammengefasst. Schauen wir uns nun den ersten Hauptsatz der Thermodynamik an. Zunächst ein Video zur Einführung:
Für ein geschlossenes System gilt
$$W_{V,12} + Q_{12} = \Delta U_{12} + \Delta E_{kin} + \Delta E_{pot}$$
Die Zu- und oder Abfuhr von Wärme und Energie führt zu einer Änderung der Energie des Systems. Der erste Hauptsatz der Thermodynamik kann deshalb als Energieerhaltungssatz verstanden werden: Energie kann nicht vernichtet werden, sie bewegt sich nur in oder aus Systemen und verändert dabei deren Energieniveau.
Im weiteren Verlauf dieses Artikels werden wir die mechanischen Energien (potentiell und kinetisch) vernachlässigen. Potentielle Energie ist bei Anwendungen, die sich näherungsweise auf einem Höhenniveau befinden, vernachlässigbar. Die Systeme, die wir in den Beispielen betrachten werden, bewegen sich nicht, weshalb wir kinetische Energie ebenfalls vernachlässigen. Teilen wir die Gleichung oben durch die Masse, erhalten wir den vereinfachten ersten Hauptsatz der Thermodynamik für geschlossene Systeme in spezifischer Form
$$w_{v,12} + q_{12} = \Delta u_{12}$$
19,99€
Offene Systeme – Ersten Hauptsatz der Thermodynamik erweitern
Für offene Systeme müssen wir den ersten Hauptsatz erweitern. Stellen wir uns die Turbine innerhalb eines Dampfkraftkreislaufes vor, durch die ein Massestrom $\dot{m}$ stationär strömt (die Turbine ist also schon angefahren worden). Neben den bisher besprochenen Energieformen weist dieses System sogenannte Verschiebearbeiten auf.
Es ist Energie notwendig, um vorne in der Turbine bestehenden Dampf zu verdrängen und ihn hinten aus der Turbine herauszudrücken. Diese Verschiebearbeiten müssen zusätzlich berücksichtigt werden. Sie werden definiert als die Änderung des Produktes aus Druck und spezifischem Volumen
Verschiebearbeit an offenen Systemen: $\delta (p \cdot v) $
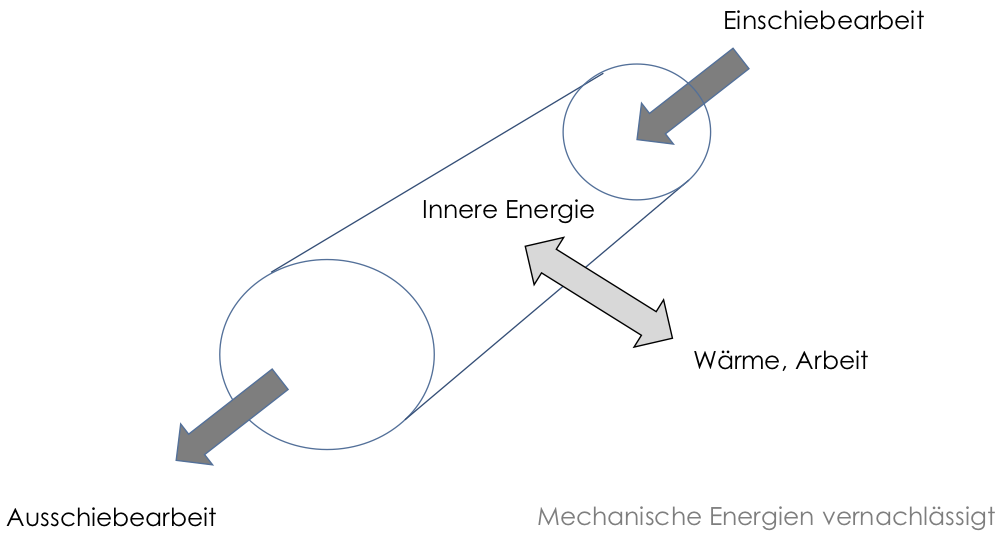
Außerdem werden bei offenen Systemen die Arbeit und Wärme mit dem durchlaufenden Massestrom multipliziert, wodurch sich ein Wärmestrom und die Leistung als Energien pro Zeit ergeben:
Wärmestrom: $\dot{Q} = q \cdot \dot{m}$
Leistung: $P= w_t \cdot \dot{m}$
Damit folgt für den ersten Hauptsatz offener Systeme
$$P_{12} + \dot{Q}_{12} = \dot{m} \cdot [ \Delta u_{12} + \delta(p \cdot v)]$$
Die Verschiebearbeit erscheint in der Gleichung oben etwas unhandlich. Die Summe aus innerer Energie und Verschiebearbeit in einem Zustand des offenen Systems wird deshalb als Enthalpie $h$ definiert
$$h = u + p \cdot v$$
Der Zusammenhang von Enthalpie und innerer Energie ist abhängig von der Zustandsänderung. Allgemein gilt für eine Zustandsänderung
$$\delta h = \delta u + \delta (p \cdot v)$$
Differentialgleichungen bemühen wir hier nur im äußersten Notfall. Für isobare und isochore Zustandsänderungen können wir ausnutzen, dass sich das Produkt aus Druck und spezifischem Volumen jeweils nur in einer Zustandsgröße ändert. Für isochore Zustandsänderungen gilt also beispielsweise
$$\Delta h_{12} = \Delta u_{12} + (v \cdot p_2 – v \cdot p_1 ) = \Delta u_{12} + v \cdot (p_2 – p_1) $$
Das werden wir später wieder nutzen. Verwenden wir die Enthalpie, lautet der erste Hauptsatz für offene Systeme also:
$$P_{12} + \dot{Q}_{12} = \dot{m} \cdot \Delta H$$
Der erste Hauptsatz der Thermodynamik erklärt nicht alles
Der erste Hauptsatz führt Arbeit und Wärme in Systeme und ändert dadurch deren Energie. Im Umkehrschluss kann jede Absenkung der Energie des Systems wieder als Arbeit oder Wärme entnommen werden. Die praktische Erfahrung zeigt, dass das so nicht stimmen kann. Wenn ich einen Topf mit Wasser auf einem Herd zum Kochen bringe, kann ich die Wärme im Topf wieder vollständig als elektrische Energie zurückgewinnen? Wenn ich ein Pendel anstoße, hört es dann von alleine nie auf zu schwingen?
Wir müssen den ersten Hauptsatz einschränken, weil er uns Möglichkeiten suggeriert, die wir technisch nicht umsetzen können.
Technische Prozesse unterliegen Dissipation (von lat.“dissipare“ zerstreuen). In einen Prozess eingebrachte Energie (z.B. die Arbeit, um ein Pendel auszulenken oder die Wärme, um einen Topf voll Wasser zu erwärmen) wird nicht vollständig zu diesem Zweck eingesetzt, sondern geht teilweise „verloren“. So bewirkt die Reibung in der Lagerung des Pendels und gegen die Luft eine Gegenkraft, die über die Drehbewegung zu einer Energieabgabe in Form von Wärme führt und das Pendel damit bis in die Ruhelage abbremst. Analog geht beim Wassertopf die Wärme teilweise über Wärmeleitung an die Luft „verloren“ und wird nicht zum Erhitzen des Wassers genutzt.
Wichtig
Energie geht nur im Sinne der technischen Anwendung verloren! Sie verschwindet jedoch nicht, sondern fließt in eine andere Richtung zweckfremd ab. Dass Energie verloren geht, werden wir als Ausdruck im Weiteren vermeiden und stattdessen von Dissipation sprechen.
In Bezug auf die Dissipation ist ein weiteres lateinisches Fremdwort von Bedeutung: Die Irreversibilität.
Irreversibilität
Die Unumkehrbarkeit (einer Zustandsänderung). Demgegenüber sind reversible Zustandsänderungen idealtypisch. Die Luft in einer Pumpe wird durch Volumenänderungsarbeit verdichtet und ändert dadurch Druck, Volumen und spezifische Dichte. Wird die Zustandsänderung durch Expansion der Luft rückgängig gemacht, wird die eingesetzte Volumenänderungsarbeit zurückgewonnen und die Ausgangszustandsgrößen wieder erreicht.
Reale Zustandsänderungen sind irreversibel, sie können also nicht einfach idealtypisch umgekehrt werden. In einer realen Luftpumpe wird durch Reibung an den beweglichen Bauteilen und innerhalb der Luft (die Moleküle reiben aneinander) ein Teil der eingesetzten Volumenänderungsarbeit dissipiert. Wird die Luft nach der Kompression also expandiert, wird dabei weniger Volumenänderungsarbeit abgegeben als vorher zugeführt wurde, der Rest ist dissipiert.
$$w_{V,ein} = w_{V,aus} + w_{diss}$$
Wir müssen eine Zustandsgröße definieren, anhand deren Änderung wir die Irreversibilität eines Prozesses bemessen können. Mit Hilfe so einer Zustandsgröße können wir die Anwendung des ersten Hauptsatzes um unsere Erkenntnis der Dissipation erweitern.
19,99€

