
Thermische Zustandsgleichung des idealen Gases
Für das ideale Gasgesetz müssen wir uns ein System vorstellen, in dem (vereinfachte) Teilchen eines Stoffes vorhanden sind. Diese Teilchen
- sind ausdehnungslose Punkte, die
- untereinander und mit den Wänden des Systems nur durch Stöße interagieren können
- und keine anderen (z.B. elektromagnetischen) Wechselwirkungen als diese Stöße aufweisen
19,99€
Die Teilchen liegen bei einer geringen Dichte und einem geringen Druck vor. Wir können dann näherungsweise von einem idealen Gas sprechen, dessen Verhalten sich durch das ideale Gasgesetz
$$ p\cdot V = m\cdot R \cdot T $$
beschreiben lässt. Damit liegt ein Zusammenhang zwischen den Zustandsgrößen Druck, Temperatur und spezifischem Volumen vor. Damit das Volumen in der Gleichung spezifisch wird, teilen wir beide Seiten durch die Masse des betrachteten Systems $m$
$$p \cdot \frac{V}{m} = R \cdot T \text{ bzw. } p\cdot v = R \cdot T$$
Das $R$ in der Gleichung ist die sogenannte universelle Gaskonstante in spezifischer Form. Sie wird allgemein molar definiert
$$ \text{Universelle Gaskonstante } R_{m}=8,314 \left[ \frac{\text{J}}{\text{mol K}}\right]$$
Und muss für das ideale Gasgesetz in die spezifische Gaskonstante umgerechnet werden. Hierfür wird die Molmasse verwendet, die wir in Kapitel Zustandsgrößen und Zustandsänderung kennengelernt haben. Die Molmasse gibt an, wie viel etwa $6 \cdot 10^23$ Teilchen eines Stoffes wiegen
$$R \left[ \frac{\text{J}}{\text{kg K}}\right] = \frac{R_m \ \left[ \frac{\text{J}}{\text{mol K}}\right]}{M \ \left[ \frac{\text{kg}}{\text{mol}}\right]}$$
Zustandsänderungen idealer Gase
Mit dem idealen Gasgesetz können wir die Zustandsänderungen idealer Gase berechnen. Solange wir die Annahmen von oben dabei im Blick behalten und kleine Moleküle wie Kohlenstoffdioxid oder Sauerstoff betrachten, liefert das ideale Gasgesetz gute Näherungslösungen.
Wir haben bisher isotherme, -bare und -chore Zustandsänderungen kennengelernt. Die Änderung der Zustandsgrößen können für eine isotherme Zustandsänderung von Zustand 1 nach 2 wie folgt berechnet werden. Zunächst gilt
$$p\cdot v = \underbrace{R \cdot T}_{\text{const.}}$$
Die rechte Seite der Gleichung besteht aus einer Temperatur, die bei isothermen Zustandsänderungen konstant ist und der spezifischen Gaskonstante. Die rechte Seite ist also bei isothermen Zustandsänderungen unveränderlich, das Produkt aus spezifischem Volumen und Druck vor und nach der Zustandsänderung muss demzufolge ebenfalls gleich bleiben, damit die Gleichung erfüllt ist.
$$p_1\cdot v_1 = p_2\cdot v_2$$
durch Umformen folgt
$$\frac{p_1}{p_2} =\frac{v_2}{v_1}$$
Mit Hilfe dieser Gleichung können wir ein Beispiel lösen.
Beispiel 1
Wasserstoffmoleküle als ideales Gas der Molmasse $M_{H_2}= 2,02 \frac{\text{g}}{\text{mol}}$ werden isotherm ausgehend vom Umgebungsdruck verdichtet. 1 $\text{kg} \ H_2$ befindet sich in einem Kolben des Volumens $V = 10 \ \text{l}$, dessen Volumen durch eine Verdichtung halbiert wird. Welchen Wert hat die spezifische Gaskonstante und wie groß ist der Druck nach der Verdichtung?
Wir berechnen die spezifische Gaskonstante von $H_2$:
$$ R_{H_2}= \frac{R_m}{M} = \frac{8{,}314 \frac{\text{J}}{\text{molK}}}{2{,}02 \cdot 10^{-3} \frac{\text{kg}}{\text{mol}}} \approx 4115{,}84 \frac{\text{J}}{\text{kgK}}$$
und den Druck nach der isothermen Verdichtung:
$$ p_2 = \frac{v_1}{v_2} \cdot p_1 = 2 \cdot 1\ \text{bar} = 2 \ \text{bar} = 200000 \ \text{Pa}$$
Die Zusammenhänge der sich ändernden Zustandsänderungen lassen sich für isochore und isobare Zustandsänderungen herleiten, wie wir es für die isotherme Zustandsänderung gezeigt haben.
- Isochore Zustandsänderung: $\frac{T_1}{T_2} = \frac{p_1}{p_2}$
- Isobare Zustandsänderung: $\frac{T_1}{T_2} = \frac{v_1}{v_2}$
Außerdem findet sich eine Zusammenfassung mit Beispielen im Video.
Isotherme Zustandsänderung:
Isochore Zustandsänderung:
Isobare Zustandsänderung:
Polytrope Zustandsänderung
Bisher haben wir mit dem idealen Gasgesetz Zustandsänderungen bei konstantem Druck, Volumen oder konstanter Temperatur berechnet. Wie lassen sich jedoch Zustandsänderungen berechnen, bei denen sich alle drei Zustandsgrößen ändern?
Wir definieren polytrope (von gr. „polus“ mehrere) Zustandsänderungen mit einem sogenannten Polytropenexponenten $n$:
Polytrope Zustandsänderung: $p \cdot v^n = \text{const.}$
Der Polytropenexponent wird für ideale Gase als Materialkonstante angegeben. Für polytrope Zustandsänderungen können wir die Verhältnisse von Druck und Temperatur bzw. Volumen wie folgt berechnen
$$\frac{p_2}{p_1}= \left( \frac{v_1}{v_2} \right)^2 = \left( \frac{T_1}{T_2} \right)^{\frac{n}{1-n}}$$
Reversibel adiabate Zustandsänderung
Bevor wir den Abschnitt zum idealen Gasgesetz mit einem großen Beispiel abschließen, müssen wir eine fünfte Art der Zustandsänderung einführen.
Stellen wir uns vor, wie Luft in einer Pumpe verdichtet wird. Es ist nicht schwer zu glauben, dass dabei in einer realen Pumpe Energie etwa durch Reibung „verloren“ geht (im nächsten Kapitel werden wir sehen, dass Energie nicht verschwinden kann). Reibung wird in Form von Wärme an die Umgebung abgegeben. Bei sogenannten reversibel adiabaten Zustandsänderungen geschieht dies nicht, sie sind idealtypisch. Es gilt:
- reversibel: durch eine Umkehrung des Prozesses lässt sich der Ausgangszustand (verlustfrei) wiederherstellen
- adiabat: es wird keine Wärme während der Zustandsänderung (etwa in Form von Reibungswärme) abgegeben.
Reversibel adiabate Zustandsänderungen sind technisch perfekt, sie existieren aber leider nicht. Trotzdem sind sie nützlich, um anhand des optimalen Prozesses die Wirkung realer Maschinen zu bewerten. Zur Berechnung reversibel adiabater Zustandsänderungen behelfen wir uns wie bei den polytropen Zustandsänderungen einer Materialkonstante, dem Isentropenexponenten $\kappa$ (sprich Kappa).
Es gilt für reversibel adiabate Zustandsänderungen
$$p \cdot v^{\kappa} = \text{const.}$$
und damit analog zu den polytropen Zustandsänderungen
$$\frac{p_2}{p_1}= \left( \frac{v_1}{v_2} \right)^{\kappa} = \left( \frac{T_1}{T_2} \right)^{\frac{\kappa}{1-\kappa}}$$
Übrigens: reversibel adiabate Zustandsänderungen sind gleichzeitig sogenannte isentrope Zustandsänderungen. Das Wort isentrop setzt sich zusammen aus Entropie und der Silbe „iso“ (griechisch für gleich). Die Entropie ist eine Zustandsgröße.
Realgasfaktor
Zu Beginn des Abschnitts haben wir Annahmen getroffen, bei deren Erfüllung näherungsweise das ideale Gasgesetz gilt. Abschließend definieren wir den Realgasfaktor, um prüfen zu können, wie gut das ideale Gasgesetz Zustandsänderungen beschreiben kann.
Realgasfaktor: $z = \frac{p \cdot v}{R \cdot T}$
Für einen beliebigen Stoff und Zustand werden die drei Zustandsgrößen und die spezifische Gaskonstante ermittelt und $z$ berechnet. Liegt $z$ nahe bei 1, verhält sich der Stoff wie ein ideales Gas.
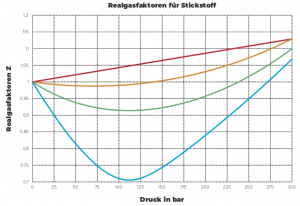
Es kann gezeigt werden, dass für einfache Moleküle bei niedrigen Dichten und Drücken $z$ tatsächlich nahe bei 1 bleibt.
19,99€

