
Zustandsgrößen
In der Thermodynamik wird in Systemen gearbeitet, in denen sich Zustandsgrößen verändern. Dabei gibt es eine Menge unterschiedlicher Systeme und Zustandsgrößen. Das schauen wir uns im ersten Abschnitt an.
Der Druck und die Temperatur sind zwei Zustandsgrößen, die uns in verschiedenen Zusammenhängen begegnen werden. Da Amerikaner und Europäer diese beiden Größen unterschiedlich messen und wir am Ende mit einer ganz anderen Einheit rechnen werden, widmen wir diesen beiden Zustandsgrößen den zweiten Abschnitt.
Die Zustandsgrößen eines Systems sind nicht in Stein gemeißelt. Tatsächlich wird Thermodynamik erst wirklich interessant, wenn sie sich ändern. Hierfür schauen wir uns im dritten Abschnitt Zustandsänderungen an.
19,99€
Ein Unterschied zwischen Volumen und Temperatur
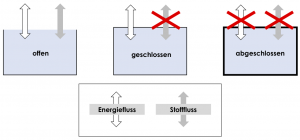
In der Thermodynamik werden üblicherweise Prozesse betrachtet, in denen Energie irgendetwas verändert. Es heißt ja schon Thermo-Dynamik (von griechisch „thermós“ warm und „dynamis“ Kraft). Hierfür definieren wir zuerst drei Arten von Systemen, in dem wir Veränderungen beobachten.
- Offenes System: Ein System, das Energie und Materie mit seiner Umgebung austauschen kann, z.B. ein offener Kochtopf
- Geschlossenes System: Ein System, das Energie mit seiner Umgebung austauschen kann, z.B. ein perfekt dichter Stahlbehälter
- Abgeschlossenes System: Ein System, das weder Energie noch Materie mit seiner Umgebung tauschen kann. Solche Systeme gibt es nur theoretisch, da in technischen Anwendungen ein Wärmestrom in oder aus dem System nie ganz verhindert werden kann. Bei einem abgeschlossenen System reicht es aber vorerst, sich eine perfekt dichte und isolierte Thermoskanne vorzustellen.
In thermodynamischen Systemen befindet sich Materie, deren Zustand wir beschreiben wollen. Dafür nutzen wir konsequenterweise sogenannte Zustandsgrößen. Wir definieren zunächst einige thermodynamische Zustandsgrößen, die wir später um weitere Zustandsgrößen ergänzen werden:
- Druck (Formelzeichen $p$ von engl. Pressure)
- Temperatur (Formelzeichen $T$)
- Volumen (Formelzeichen $V$)
- Masse (Formelzeichen $m$)
Diese Zustandsgrößen werden in sehr unterschiedlichen Einheiten skaliert, je nachdem, wo auf der Welt wir uns befinden. Diese Einheiten sind historisch gewachsen, für uns Europäer aber oft nicht intuitiv. In Bar haben wir ein Gefühl für unseren Reifendruck, in Torr oder Psi aber eher nicht. Wir schauen uns die unterschiedlichen Einheiten im nächsten Abschnitt an und erweitern nun zunächst die Grundlagen.
Intensive und extensive Zustandsgrößen
Wir haben vor uns ein System der Masse $m$ , dem Druck $p$, der Temperatur $T$ und dem Volumen $V$. Was passiert mit diesen Zustandsgrößen, wenn wir das System in der Mitte teilen? Einige Größen bleiben unverändert, wie der Druck oder die Temperatur. Solche Zustandsgrößen werden als intensiv bezeichnet. Zustandsgrößen wie Masse und Volumen, die sich bei einer Teilung des Systems ändern, werden als extensiv bezeichnet.
- Intensiv: unabhängig von einer Systemteilung, wie Druck und Temperatur
- Extensiv: abhängig von einer Systemteilung, wie Masse und Volumen
Spezifische Zustandsgrößen
Um die extensiven Zustandsgrößen unterschiedlicher Systeme zu vergleichen, können diese auf die Systemmasse bezogen werden. Wir können das sogenannte spezifische Volumen als Kehrwert der Dichte $ \rho = \frac{m}{V} \ \left[\frac{\text{kg}}{\text{m}^3}\right]$ definieren:
Spezifisches Volumen: $v= \frac{1}{\rho} = \frac{V}{m} \left[\frac{\text{m}^3}{\text{kg}} \right]$
Wir haben Thermodynamik als Energielehre eingeführt. Es ist deshalb konsequent, an dieser Stelle auch Energie zu betrachten. Ein Maß für die in einem geschlossenen System enthaltene Energie ist die innere Energie $U$, die in Joule gemessen wird. Die innere Energie ist eine extensive Zustandsgröße, die wir spezifisch definieren können.
Spezifische innere Energie: $ u=\frac{U}{m} \left[\frac{\text{J}}{\text{kg}} \right]$
Spezifische Zustandsgrößen werden im Gegensatz zu nicht spezifischen Zustandsgrößen in Kleinbuchstaben dargestellt.
19,99€
Molare Zustandsgrößen
Chemiker berechnen Reaktionsgleichungen gerne in Mol, einer Dimension, die dem Ingenieur erfahrungsgemäß unheimlich bleibt. Ganz ohne das Mol kommen wir in diesem Heft aber nicht aus und definieren es deshalb. Wir stellen uns vor, dass sich jemand die Mühe macht, die Anzahl Atome in $12\ \text{g}$ eines bestimmten Kohlenstoffs zu zählen (ernst gemeint!) und dabei auf folgende Zahl kommt
Dies ist die sogenannte Avogadro-Konstante. 1 Mol eines Stoffes enthält somit $6 \cdot 10^{23}$ Teilchen. Die Stoffmenge $n$ in Mol eines Stoffes erhalten wir, wenn wir die Anzahl Teilchen in einem System durch die Avogrado-Konstant teilen. Die Stoffmenge gibt an, wie viel Mol, also das wie vielfache der Avogadro Konstante an Teilchen in einem System enthalten sind ($n = 3$ Mol wären also etwa $18\cdot 10^{23}$ Teilchen).
Für uns interessant ist insbesondere die Molmasse $M$. Sie gibt an, wie viel ein Mol eines Stoffes wiegt. Da das Mol die Anzahl Teilchen erfasst und diese je nach Stoff unterschiedlich schwer sind, ergeben sich also unterschiedliche Molmassen.
So wie die Masse eines Moleküls pro Mol angegeben werden kann, können extensive Zustandsgrößen wie die innere Energie ebenfalls molar, also pro Mol angegeben werden
Wir können also ein thermodynamisches Problem in ein System stecken und dieses System anhand von Zustandsgrößen beschreiben. Im nächsten Abschnitt schauen wir uns an, in welchen Einheiten (oder Dimensionen) zwei der wichtigsten thermodynamischen Zustandsgrößen, nämlich Druck und Temperatur, gemessen werden können.
19,99€

