
Exergie und Anergie
In diesem Artikel beschäftigen wir uns mit der Exergie und der Anergie. Zusammengefasst kann gesagt werden, dass sie den nutzbaren und nicht-nutzbaren Teil von Wärme beschreiben. Eine genaue Beschreibung von Exergie und Anergie findest du im folgenden Artikel.
Inhaltsangabe
Wir haben bereits kennengelernt, dass Wärme nur von Systemen höherer Entropie zu Systemen niedrigerer Entropie fließen kann. Wärme fließt von wärmeren zu kälteren Temperaturen. Diese unumkehrbare Tatsache hat leider eine Konsequenz für die Verwendbarkeit von Wärme als Energieträger in technischen Systemen.
19,99€
Übersicht Exergie und Anergie
Wir können uns einen Tank mit $40°\text{C}$ warmen Wasser vorstellen. Mit Hilfe der Wärmekapazität können wir näherungsweise bestimmen, wie viel Wärme der Tank enthält (näherungsweise, weil Wärmekapazitäten nur für ideale Gase konstant sind). Die so berechnete Wärmemenge ist aber trügerisch, denn wir können sie technisch nicht vollständig nutzen, um damit einen Raum zu erwärmen. Ist der Raum $25°\text{C}$ warm, können wir das Wasser im Tank durch Wärmeabgabe an den Raum so lange nutzen, bis es im thermodynamischen Gleichgewicht mit der Umgebung steht, die Temperaturen also gleich sind. Die dann noch im Tank befindliche Wärmemenge ist nicht mehr zum Heizen nutzbar! Ist die Umgebungsluft bereits $40°\text{C}$ warm, können wir sogar gar nichts von der Wärme im Wassertank nutzen.
Wärme ist eine entropiebehaftete Größe. Entropiebehaftete Größen wie Wärme sind nicht in jeder Umgebung vollumfänglich in andere Energieformen umwandelbar. Wir müssen deshalb unsere Vorstellung von Wärme präzisieren und teilen die Wärme in zwei Teile:
- Exergie: der Teil der Wärme, der durch Abkühlung bis auf Umgebungstemperatur technisch nutzbar ist
- Anergie: die verbleibende Wärmemenge ist zwar als Energie vorhanden, kann jedoch aufgrund der Bedingung des zweiten Hauptsatzes nicht genutzt werden
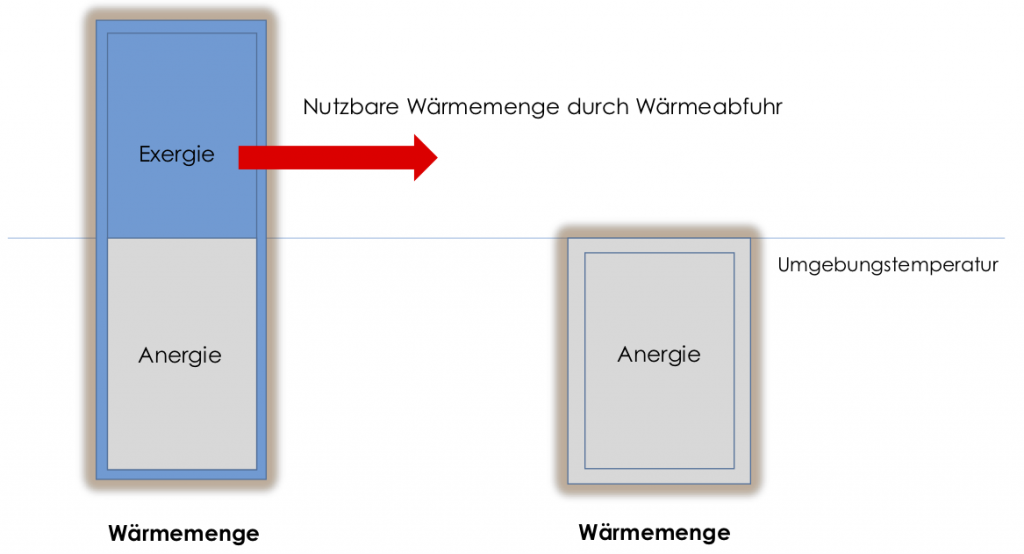
Der Anteil der Exergie an einer Wärmemenge muss berechnet werden. Hierfür stellen wir zwei unterschiedliche Konzepte vor.
Die Exergie eines Stoffstromes
Wer eine Heizung auslegen will, sollte sich mit Exergie beschäftigen. Wir stellen uns eine Rohrleitung im Vorlauf eines Heizkörpers vor, der einen $20°\text{C}$ warmen Raum weiter aufheizen soll. Wie viel Exergie transportiert das Wasser im Vorlauf?
Der erste Hauptsatz für ein offenes System wie den Vorlauf lautet (wie gewohnt unter Vernachlässigung der mechanischen Energieformen):
$$\dot{Q} + P = \dot{m} \cdot \Delta h$$
Der Wasserstrom transportiert Wärme, ohne dabei Arbeit zu verrichten. Der Wärmestrom entspricht also der Enthalpiedifferenz mal dem Stoffstrom:
$$\dot{Q}= \dot{m} \cdot \Delta h$$
Der Exergiestrom $\dot{E}$ muss nun der Wärmestrom abzüglich der mitgeführten Anergie $a$ sein.
$$\dot{E}= \dot{m} \cdot (\Delta h – a)$$
Die Anergie ist die Wärmemenge bei Umgebungstemperatur. Die Wärme ist über die Temperatur mit der Entropie verknüpft:
$$a= T_u \cdot \Delta s$$
Der Exergiestrom eines Wärmestroms ist also
$$\dot{E} = \dot{m} \cdot ( \Delta h- T_u \cdot \Delta s)$$
wobei die Differenz der Enthalpie und Entropie am Ein- und Ausgang des offenen Systems bestimmt werden muss. Für ein ideales Gas kann der Exergiestrom wie folgt berechnet werden
$$\dot{E} = \dot{m} \cdot \left( c_p \cdot \Delta T – T_u \cdot \left[ c_p \cdot \ln \left( \frac{T_2}{T_1} \right) – R \cdot \ln \left( \frac{p_2}{p_1} \right) \right] \right)$$
Die Gleichung zu Berechnung der Enthalpiedifferenz ist die kalorische Zustandsgleichung. Lassen wir also ein ideales Gas durch ein Rohr fließen, können wir berechnen, wie groß die dabei transportierte Exergie ist.
Beispielvideo Exergie eines Stoffstroms
Die Exergie einer Wärmemenge können wir berechnen. Dabei stellt sich die Frage, wie viel Exergie eigentlich in Arbeit steckt. Die Antwort darauf ist sehr einfach, weil Arbeit aus reiner Exergie besteht. Arbeit kann unabhängig von der Umgebungstemperatur aber abgesehen von unvermeidbaren Dissipationsverlusten in andere Energieformen umgesetzt werden.
Wir wissen nun, dass für technische Prozesse, die Wärme nutzen, der Exergieanteil entscheidend ist. Bevor wir uns im nächsten Kapitel Kreislaufprozessen widmen, in denen Wärme genutzt wird, um daraus Arbeit zu gewinnen, schauen wir uns Wärmeübertragung an. Das Wissen über den nutzbaren Anteil von Wärme wird erst dann interessant, wenn wir wissen, wie die Wärme überhaupt von $A$ nach $B$ kommt.
Die Wärmeübertragung hat sich aus der Thermodynamik entwickelt, ist jedoch mittlerweile eine selbstständige ingenieurwissenschaftliche Disziplin und wird hier nur kurz vorgestellt.
Konvektion, Wärmeleitung und Strahlung
In diesem Abschnitt stellen wir die drei Mechanismen vor, über die Wärme übertragen werden kann. Wer sich für seine Klausur nicht mit Wärmeübertragung beschäftigen muss, kann dieses Kapitel guten Gewissens überspringen. Vertiefende Literatur zur Wärmeübertragung findet sich im Anhang.
Den Raum heizen: Konvektion und Wärmeleitung
Wer die Pflanzen auf dem Fensterbrett über einem Heizkörper beobachtet, dem fällt vielleicht auf, dass sich einige Blätter leicht bewegen. Die erwärmte Luft über dem Heizkörper reduziert ihre Dichte (das kennen wir vom idealen Gasgesetz) und wird somit leichter als die Umgebungsluft. In der Konsequenz steigt sie auf und bewegt etwa Blätter einer Pflanze auf der Fensterbank. Beim Aufsteigen kühlt sie durch Wärmeaustausch mit der Umgebungsluft (vor allem am kalten Fenster) ab und sinkt dadurch wieder. Es entsteht eine Luftwalze, die permanent erwärmte Luft durch den Raum bewegt.
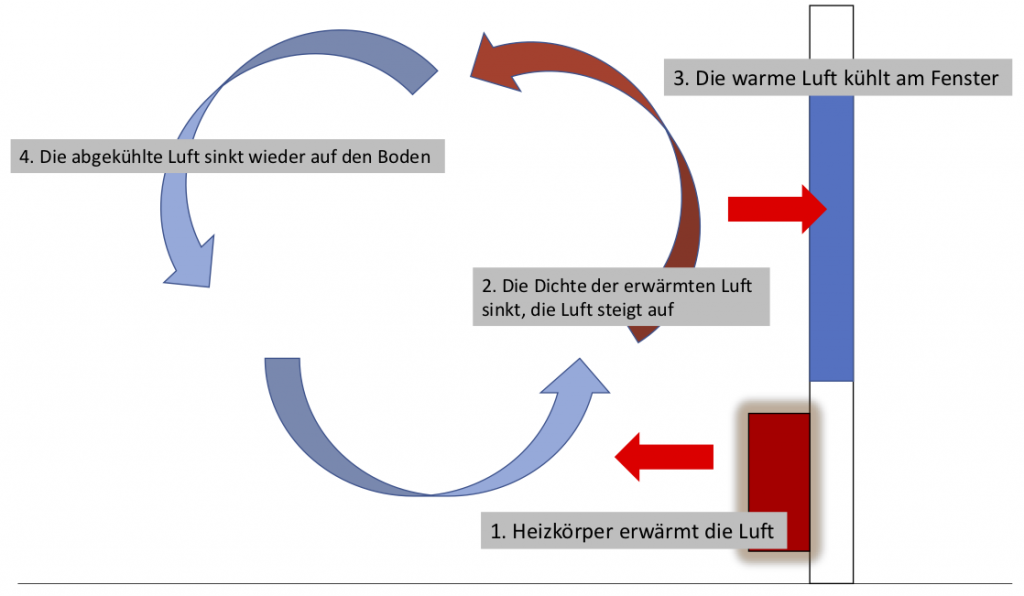
Die Übertragung von Wärme durch die Bewegung von Fluiden wird als Konvektion bezeichnet. Die oben beschriebene Konvektion wird als frei bezeichnet, weil sie selbstständig abläuft. Bewege ich heiße Luft durch ein Gebläse (wie beim Haare föhnen), wird von erzwungener Konvektion gesprochen.
Schauen wir uns die Grenzfläche zwischen Luft und Heizkörper an. Der Wärmestrom, der den Heizkörper an seiner Grenzfläche verlässt, muss gleich dem Wärmestrom sein, den die Luftbewegung an der Grenzfläche (hier definiert als $x=0$) abtransportiert
$$\dot{Q}_{Festkörper} (x=0) = \dot{Q}_{Fluid} (x=0)$$
Der Wärmestrom durch einen Festkörper an einer beliebigen Stelle ist gleich dem Produkt aus seiner Wärmeleitfähigkeit $\lambda$, seiner Querschnittsfläche $A$ und dem Temperaturgradienten $\frac{\delta T}{\delta x}$ an der betrachteten Stelle.
$$\dot{Q}_{Festkörper} = \lambda \cdot A \cdot \frac{\delta T}{\delta x}$$
Die Wärmeleitfähigkeit beschreibt, welcher Wärmestrom pro Temperaturdifferenz über eine Länge übertragen wird und hat die Dimension $\left[ \frac{\text{W}}{\text{Km}}\right]$. Der Temperaturgradient ist die Ableitung der Temperatur nach dem Weg und beschreibt somit die Änderung der Temperatur über der Länge eines Körpers. Ist ein Körper überall gleich warm, ist der Temperaturgradient also null. Anders herum kann auch nur dann Wärme durch einen Körper fließen, wenn es einen Temperaturunterschied gibt. Das passt zu unserem Verständnis des zweiten Hauptsatzes. Der Kehrwert der Wärmeleitfähigkeit ist übrigens der Wärmewiderstand eines Körpers.
Den Transport von Wärme durch einen Festkörper wird als Wärmeleitung beschreiben. Integrieren wir die Differentialgleichung für die Wärmeleitung über eine Länge $L$, erhalten wir die Gleichung zur Berechnung der Wärmeleitung unter Annahme eines linearen Temperaturgradienten:
$$\dot{Q}_{Festkörper} = \lambda \cdot A \cdot \frac{\delta T}{\delta L}$$
Kehren wir zurück zum Wärmetransport an der Grenzfläche von Festkörper und Fluid. Der Wärmestrom wird aus dem warmen Festkörper an das Fluid übertragen und berechnet sich im Fluid mit Hilfe des Wärmeübergangskoeffizienten $\alpha \left[ \frac{\text{W}}{\text{Km}^2}\right]$.
$$\dot{Q}_{Festkörper} = A \cdot \alpha \cdot \delta T$$
Der Wärmeübergangskoeffizient beschreibt, welche Wärmemenge pro Temperaturdifferenz (die Triebfeder jeder freien Wärmeübertragung) über eine Fläche $A$ fließen kann. Setzen wir nun die beiden Gleichungen der Wärmeströme an der Grenzfläche gleich folgt:
$$\lambda \cdot A \cdot \frac{\Delta T_1}{\Delta L} = A \cdot \alpha \cdot \delta T_2$$
Kürzen wir den Querschnitt und setzen $T$ als Temperatur der Grenzfläche und $T_h$ als Temperatur der Heizung, können wir näherungsweise berechnen, wie warm die Luft am Heizkörper wird:
$$T_{Luft} = \frac{\lambda \cdot (T-T_h)}{\Delta L \cdot \alpha} + T_h$$
Der Sonnenbrand: Wärmestrahlung
Wer sich im Sommerurlaub am Strand die Haut verbrennt, kommt dabei nicht mit Stoffströmen in Berührung, die den weiten Weg von der Sonne hinter sich haben und hat die Sonne auch nicht berührt. Wärme kann (auch über sehr weite Distanzen) als Strahlung übertragen werden.
Wir vertiefen die physikalischen Grundlagen (welche Strahlungsformen es gibt und wie sie aussehen) an dieser Stelle nicht weiter, sondern stellen uns Wärmestrahlen vor, die sich von einem strahlenden Körper aus durch die Luft bewegen und dabei Wärme übertragen. Wenn Sie dies tun, lässt sich der durch sie übertragene Wärmestrom annähern durch
$$\dot{Q} = A \cdot \sigma \cdot T^4$$
Die Gleichung wird als Stefan Boltzmann Gesetz bezeichnet, darin ist $T$ die Temperatur des strahlenden Körpers, $A$ der Querschnitt, durch den die Strahlung emittiert (ausgestrahlt) wird und $\sigma$ eine Naturkonstante (wie das Gesetz zur Wärmestrahlung benannt nach ihren Entdeckern). Bemerkenswert ist, dass die Wärmemenge, die ein Körper emittiert, um den Faktor 16 ($2^4$) steigt, wenn sich die Temperatur verdoppelt.
Nach diesem kleinen Exkurs kennen wir nun die grundlegenden Mechanismen der Wärmeübertragung. Vertiefende Literatur für all diejenigen, die sich intensiver mit diesem Themengebiet beschäftigen möchten, findet sich im Anhang.
19,99€

