
Der zweite Hauptsatz der Thermodynamik
Der zweite Hauptsatz der Thermodynamik wird auch Entropiesatz der Thermodynamik genannt. Warum? Das erklären wir dir im folgenden Artikel ganz genau. Hierfür haben wir das Thema so verständlich wie möglich für euch niedergeschrieben und mit Lernvideos ergänzt.
Inhaltsangabe
- Entropieänderungen bei Zustandsänderungen idealer Gase
- Entropieänderungen bei Mischungen idealer Gase
- Das T,s-Diagramm
Schauen wir uns zunächst ein Einführungsvideo zum zweiten Hauptsatz der Thermodynamik an:
Um dies über die Änderung einer Zustandsgröße zu quantifizieren, führen wir die Zustandsgröße Entropie ein. Die Entropie ist eine in der Vorstellung etwas unhandliche Zustandsgröße und wird von Chemikern, Physikern und Ingenieuren manchmal unterschiedlich verstanden. Wir entscheiden uns hier für zwei wesentliche Dinge, für die wir die Entropie einsetzen:
Die Irreversibilität von Zustandsänderungen wird über eine Änderung der Entropie dargestellt. Eine reversible Zustandsänderung führt bei ihrer Umkehrung zur Entropie wie im Ausgangszustand. Irreversible Zustandsänderungen weisen bei einer Wiederherstellung der Ausgangszustandsgrößen (z.B. Kolben der Pumpe wieder auf Ausgangsvolumen verfahren) eine veränderte Entropie auf.
Die Entropie ist eng mit der Wärme verknüpft, wie wir noch sehen werden. Der erste Hauptsatz setzt der Einsetzbarkeit von Wärme keine Grenze: Arbeit kann beliebig in Wärme umgesetzt werden und anders herum. Abgesehen von der Dissipation, mit der wir uns schon beschäftigt haben, ist Wärme noch aus einem anderen Grund nur begrenzt einsetzbar:
Wärme fließt immer nur von höheren zu niedrigeren Temperaturen: eine kalte Dose in meiner Hand führt keine „Kälte“ (ohnehin ein Wort, das wir hier nicht nutzen) ab, sondern es fließt Wärme von meiner Hand (die wärmer ist) in diese kältere Dose. Über die Entropie betrachtet können wir sagen: die Wärme fließt stets von Systemen höherer Temperaturen (und Entropien) zu kälteren Systemen niedrigerer Temperaturen (und Entropien).
Die Änderung der Entropie ist über die Änderung der Arbeit, die an einem System verrichtet wird, mit dem ersten Hauptsatz verknüpft. Diese Verknüpfung führt uns zum zweiten Hauptsatz der Thermodynamik für geschlossene Systeme
$$\text{d}s = \frac{\text{d}u + p\text{d}v}{T}$$
Wir stellen fest, dass der zweite Hauptsatz als Differentialgleichung definiert ist, obwohl doch versprochen war, das zu vermeiden. Das liegt daran, dass die Entropie entgegen der bisherigen Zustandsgrößen nicht messbar ist. Sie ist eher wie ein theoretisches Konzept, um die Dissipation in Zahlen zu fassen und wird stets als Änderung berechnet.
Wir können den zweiten Hauptsatz mit Hilfe des ersten Hauptsatzes auch in Abhängigkeit der Wärmeänderung definieren. Der erste Hauptsatz für ein geschlossenes System lautet in differentieller Form:
$$\text{d}q + \text{d}q = \text{d}u $$
Die in einem geschlossenen System verrichtete Arbeit ändert das Volumen, daher gilt für den ersten Hauptsatz aufgelöst nach der Wärmeänderung:
$$\text{d}q – p\text{d}v = \text{d}u \quad \Leftrightarrow \quad \text{d}q = \text{d}u + p\text{d}v $$
Damit erhalten wir für den zweiten Hauptsatz:
$$\text{d}s = \frac{\text{d}q}{T}$$
Für ideale Gase können wir die kalorische Zustandsgleichung bemühen, die für geschlossene Systeme die Wärmeänderung liefert
$$\text{d}s = \frac{c_v \cdot \text{d}T}{T} \quad \Leftrightarrow \quad \Delta s = c_v \displaystyle\int_{T_1}^{T_2} \frac{1}{T} \ \text{d}T = c_v \cdot \ln \left( \frac{T_2}{T_1} \right)$$
Für ideale Gase ist die Entropieänderung bei einer Wärmezufuhr also handlich zu berechnen. Schauen wir uns den zweiten Hauptsatz für ein offenes System an, bei dem wir die Änderung der Enthalpie berücksichtigen müssen
$$\text{d}s = \frac{\text{d}h – v \text{d}p}{T}$$
Auch hier können wir mit dem zugehörigen ersten Hauptsatz
$$\text{d}w +\text{d}q = \text{d}h$$
die Entropieänderung für eine Wärmezufuhr bestimmen
$$\Delta s = c_p \cdot \ln \left( \frac{T_2}{T_1} \right)$$
Die Frage ist nun, wie wir den zweiten Hauptsatz als Differentialgleichung lösen können, wenn zusätzlich Arbeit an einem System verrichtet wird.
19,99€
Entropieänderungen bei Zustandsänderungen idealer Gase
Die Luft in unserer oft zitierten Luftpumpe wird gleichzeitig erwärmt und verdichtet. Wie ändert sich dabei die Entropie der enthaltenen Luft?
Der zweite Hauptsatz lautet für geschlossene Systeme
$$\text{d} s =\frac{\text{d}u + p \text{d} v}{T}$$
Um die Differentialgleichung integrieren zu können, müssen wir die innere Energie wie gehabt durch die kalorische Zustandsgleichung umformulieren und trennen den Bruch nach den beiden Zählern
$$\text{d} s =\frac{\text{d}u}{T} + \frac{p \text{d} v}{T} = c_v \cdot\frac{1}{T} \text{d}t + \frac{p}{T} \text{d}v$$
Für den zweiten Term können wir das ideale Gasgesetz ausnutzen $p \cdot v = R \cdot T \quad \Leftrightarrow\quad \frac{p}{T} = R \cdot \frac{1}{v}$ und erhalten damit
$$\text{d} s =c_v \cdot\frac{1}{T} \text{d}t + R \cdot \frac{1}{v} \text{d}v \quad \Leftrightarrow \quad \Delta s = c_v \cdot \ln \left(\frac{T_2}{T_1} \right) + R \cdot \ln \left(\frac{v_2}{v_1} \right)$$
Für die Entropieänderung bei Zustandsänderungen idealer Gase in geschlossenen Systeme. Ist das System offen, lautet die Formel
$$\Delta s =c_p \cdot \ln \left( \frac{T_2}{T_1} \right) + R \cdot \ln \left( \frac{p_2}{p_1} \right)$$
Die Entropie ändert sich also gemäß den beiden Gleichungen, wenn wir ein ideales Gas reversibel im Zustand ändern. Zustandsänderungen idealer Gase sind in diesem Heft immer reversibel.
Wichtig
Die Entropie kann sich auch bei reversiblen Zustandsänderungen ändern. Sie ändert sich jedoch bei Hin und Rückzustandsänderung betragsmäßig gleich. Ändert sie sich betragsmäßig unterschiedlich, wird darüber die Irreversibilität der Reaktion bemessen.
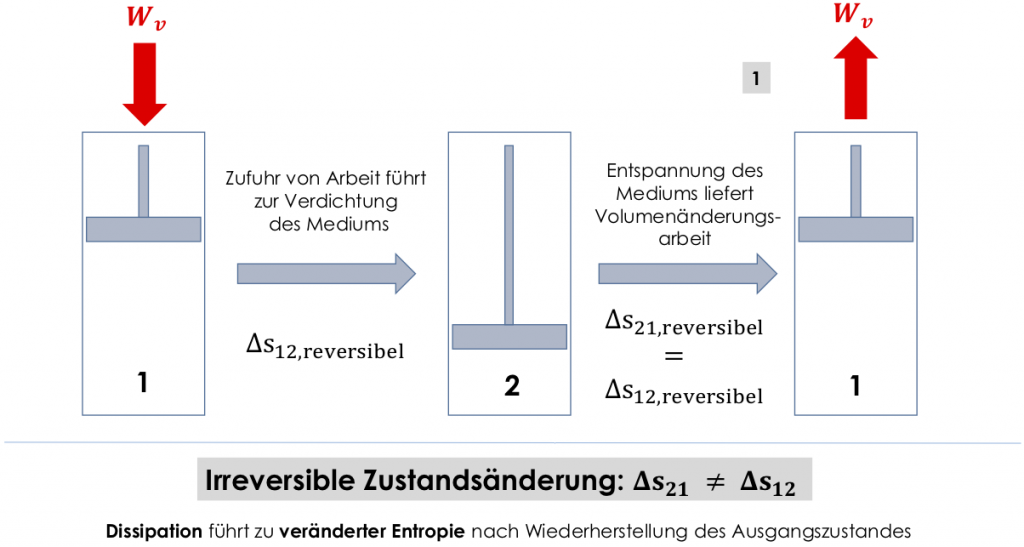
Bevor wir die Entropie anhand eins neuen Diagramms verinnerlichen, das wir später wieder brauchen werden, schauen wir uns kurz Mischungen an. In der Verfahrenstechnik werden ständig Komponenten gemischt. Um sich der Thermodynamik solcher Prozesse (sehr sanft) zu nähern, schauen wir uns die Entropiezunahme bei der Mischung idealer Gase an.
Entropieänderungen bei Mischungen idealer Gase
Werden zwei Substanzen vermischt, können wir zunächst die resultierenden Massen und Energien bilanzieren wie bisher
$$m_{ges}=m_1 + m_2 \quad \text{bzw.} \quad u_{ges} \cdot m_{ges}=u_1 \cdot m_1 + u_2 \cdot m_2$$
Achtung: Es gilt keine „Entropieerhaltung“!
$$S_{ges} > s_1 \cdot m_1 + s_2 \cdot m_2$$
Werden zwei Substanzen vermischt, ist die resultierende Entropie der Mischung also größer als die Summe der Entropien der Einzelkomponenten. Es lässt sich jedoch genau ein Fall herleiten, für den die Entropie der Mischung genau gleich der Entropie der Einzelkomponenten ist. Wir mischen zwei ideale Gase mit konstanter Wärmekapazität
$$S_1+ S_2 = m_1 \cdot \left[ c_v \cdot \ln \left( \frac{T_1}{T_0} \right) + R \cdot \ln \left( \frac{v_1}{v_0} \right) \right] + m_2 \cdot \left[ c_v \cdot \ln \left( \frac{T_2}{T_0} \right) + R \cdot \ln \left( \frac{v_2}{v_0} \right) \right] $$
Die Gleichung ist also nichts anderes als die Summe der Einzelentropien, die jeweils bezogen auf einen Referenzzustand (Index 0) berechnet werden. Mit Hilfe der Massen- und Energiebilanz sowie der Potenzgesetze lässt sich hieraus die irreversible Entropiezunahme bei der Mischung idealer Gase herleiten
$$\Delta S_{irr} = c_v \cdot \ln \left[ \frac{ \left( \frac{m_1}{m_1 + m_2} \cdot T_1 + \frac{m_2}{m_1 + m_2} \cdot T_2 \right) ^{m_1+m_2}}{T_1^{m_1} \cdot T_2^{m_2}} \right] + R \cdot \ln \left[ \frac{ \left( \frac{m_1}{m_1 + m_2} \cdot v_1 + \frac{m_2}{m_1 + m_2} \cdot v_2 \right) ^{m_1+m_2}}{v_1^{m_1} \cdot v_2^{m_2}} \right] $$
Falls Temperaturen und Volumina in den Komponenten gleich waren ($T_1=T_2=T$) vereinfacht sich die Gleichung zu
$$S_{ges} = (m_1 + m_2 ) \cdot \left[ c_v \cdot \ln \left( \frac{T}{T_0}\right) + R \cdot \ln \left( \frac{v}{v_0}\right) \right]$$
Anschaulich: Mische ich ein Fluid im gleichem Ausgangszustand, ist die resultierende Entropie die über die Massenanteile gewichtete Entropie der Einzelkomponenten. Muss die Entropiezunahme für unterschiedliche thermodynamische Ausgangszustände berechnet werden, ist die obere große Gleichung erforderlich.
19,99€
Das T,s-Diagramm
Bisher haben wir die Zustandsänderungen idealer Gase im $p,v$-Diagramm dargestellt. Dort können wir die technische und Volumenänderungsarbeit darstellen.
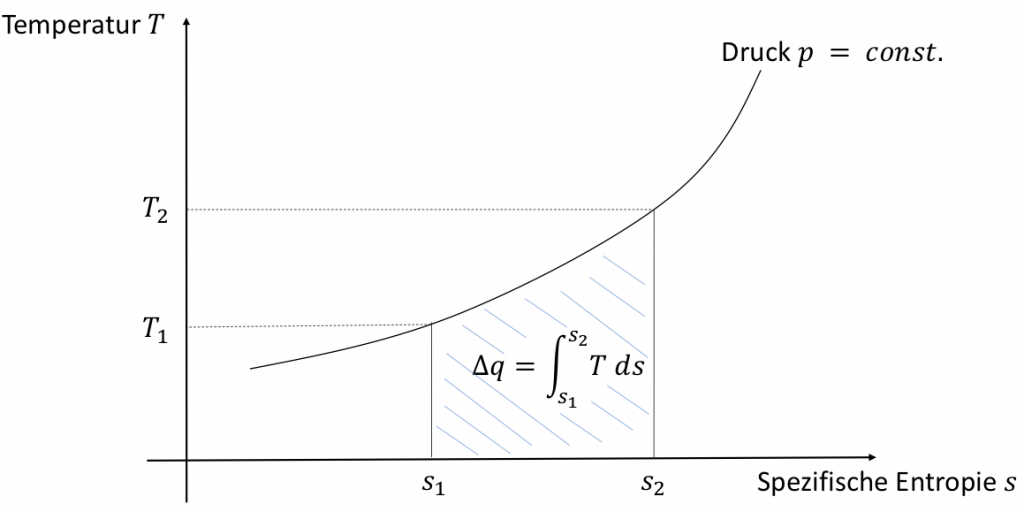
Im vorherigen Abschnitt haben wir gesehen, dass die Entropie mit der Wärme und damit im Fall idealer Gase direkt mit der Temperatur verknüpft ist. Zustandsänderungen idealer Gase können in einem sogenannten $T,s$-Diagramm dargestellt werden. In so einem Diagramm verlaufen Isobaren der Zustandsänderungen idealer Gase wie in der Abbildung zu sehen. Erwärmen wir ein System isobar, können wir die zugeführte Wärmemenge als Fläche unter der Isobare einzeichnen.
$$\text{d}s =\frac{\text{d}u + p \text{d}v }{T} = \frac{\text{d}q}{T} \quad \Leftrightarrow \quad \text{d}q = T \text{d}s \quad \Leftrightarrow \quad \Delta q = \displaystyle\int_{T_1}^{T_2} T \ \text{d}s$$
Nach so viel Theorie und Gleichungen wird im letzten Abschnitt dieses Kapitels Zeit für ein paar Beispielaufgaben zum selbstständigen Vertiefen.
Beispielaufgabe Entropieänderung in einem Rohr

