
Zustandsänderung
Viele komplizierte Zusammenhänge lassen sich in Bildern und Diagrammen einfach darstellen. In der Thermodynamik lassen sich die Zustandsgrößen und deren Änderungen in Systemen in sogenannten $p,v$-Diagrammen darstellen. Der Zustand eines Systems lässt sich mit Druck, Temperatur und spezifischem Volumen eindeutig darstellen.
19,99€
Die Gleichung zeigt, dass der Zustand eines Systems eine dreidimensionale Funktion mit den Parametern $p,v$ und $T$ ist. Das ist unübersichtlich und für unsere Zwecke in Thermodynamik 1 gar nicht nötig. Der Trick ist, für das $p,v$-Diagramm Kurven konstanter Temperatur aus dem dreidimensionalen Diagramm übereinander darzustellen.
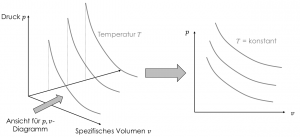
Kurven konstanter Temperatur werden als Isothermen (von gr. „isos“ gleich) bezeichnet. Die Isothermen stehen für das Verhältnis der Änderung von Druck und spezifischem Volumen bei konstanter Temperatur. Für das Beispiel in der Abbildung sehen wir, dass für eine Temperatur bei steigendem spezifischem Volumen der Druck sinkt. Unser Verständnis vom Verhalten von Stoffen werden wir fortlaufend Stück für Stück erweitern.
Ausgehend von einem festen Zustandspunkt können wir jeweils zwei Zustandsgrößen ändern, während wir die dritte Zustandsgröße festhalten. Je nachdem, welche der drei Zustandsgrößen $p,v$ oder $T$ konstant belassen wird, können wir drei Zustandsänderungen definieren und im $p,v$-Diagramm darstellen.
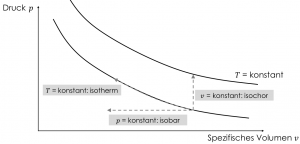
Die drei Zustandsänderungen lauten:
- Isotherme Zustandsänderung: Änderung von Druck und spezifischem Volumen bei konstanter Temperatur
- Isobare Zustandsänderung: Änderung von Temperatur und spezifischen Volumen bei konstantem Druck
- Isochore Zustandsänderung: Änderung von Temperatur und Druck bei konstantem spezifischem Volumen
Das klingt zunächst sehr theoretisch, deswegen schließen wir den Abschnitt mit einem Beispiel.
Zustandsänderungen in einer Kolbenpumpe
Hier geht es direkt zum passenden YouTube-Video:
In einem Behälter der Masse $m$ und des Volumens $V$ (woraus sich ein spezifisches Volumen $v$ ergibt) herrscht ein Druck $p$ bei einer Temperatur $T$. Der Behälter wird nun erwärmt. Um welche Zustandsänderung handelt es sich?
1. Die Temperatur steigt an, allerdings kann die Luft sich in der Pumpe infolge der Wärmezufuhr nicht ausdehnen, das Volumen bleibt also konstant. Es handelt sich um eine isochore Zustandsänderung mit steigendem Druck.
Der Behälter besitzt oben einen verschiebbaren Kolben als Deckel. Es wird weiter Wärme zugeführt. Um welche Zustandsänderung handelt es sich jetzt?
2. Die Wärmezufuhr erhöht die Temperatur der Luft. Der Kolben hebt sich, wodurch sich das Volumen ändert, das spezifische Volumen ändert sich also auch. Die Zustandsänderung ist isobar. Sobald wir Zustandsänderungen berechnen können, werden wir diese Plausibilitätsüberlegung noch mal nachrechnen und belegen.
Der Behälter wird abschließend mit weiter Luft befüllt, wodurch Druck und Temperatur und Dichte steigen. Allerdings wird nun gewartet, bis die durch die Verdichtung gestiegene Temperatur wieder auf das Ausgangsniveau gesunken ist. Ist die Zustandsänderung isotherm?
3. Es wird Luft in den Behälter gepumpt. Das spezifische Volumen und der Druck ändern sich also. Da der Vorgang so lange dauert, bis die Luft wieder auf dem Ausgangsniveau ist, kann der Vorgang (näherungsweise) als isotherm betrachtet werden.
Mit diesem Beispiel beenden wir das Kapitel zu den Grundlagen. Wir können Systeme und einige Zustandsgrößen definieren und messen und wissen, dass sich Zustandsgrößen ändern können. Im nächsten Kapitel kehren wir zur Temperatur zurück und beginnen dann, Zustandsänderungen von Systemen zu berechnen.
19,99€

