pKs- und pKb-Werte

Wenn wir zwei verschiedene Säuren mit der gleichen Konzentration betrachten, so können diese trotzdem verschiedene pH-Werte aufweisen. Warum ist das so?

Das liegt daran, dass manche Säuren stärker sind als andere, also leichter ihre Protonen abgeben können. Natürlich gibt es auch hier eine Größe, welche uns darüber Aufschluss gibt.

Es handelt sich dabei um die Säurekonstante KS bzw. den pKS-Wert. Die Säurekonstante leitet sich, genau wie das Ionenprodukt des Wassers, aus dem MWG her und ist ein Maß dafür, wie „gerne“ eine Säure ein Proton an Wasser abgibt.

Wenden wir hier wieder das MWG an, erhalten wir die folgende Gleichgewichtskonstante:

\begin{align*}
K = \frac{c({H_3O^{+}}) \cdot c({A^{-}})}{c({HA}) \cdot c({H_2O})}
\end{align*}

Auch hier können wir, wie bei dem Ionenprodukt des Wassers, die Konzentration des Wassers als annähernd konstant betrachten (da so viel vorhanden ist, dass sich bei der geringen Säuremenge die Konzentration des Wassers kaum ändert) und sie mit der Gleichgewichtskonstanten verrechnen:

\begin{align*}
\begin{array}{crcll}
& K & = & \frac{c({H_3O^{+}}) \cdot c({A^{-}})}{c({HA}) \cdot c({H_2O})} & |\cdot c({H_2O}) \\ \\
\Leftrightarrow & K \cdot c({H_2O}) & = & \frac{c({H_3O^{+}}) \cdot c({A^{-}})}{c({HA})} & |\ \text{Setze } K \cdot c({H_2O}) = K_\text{S} \\ \\
\Rightarrow & K_\text{S} & = & \frac{c({H_3O^{+}}) \cdot c({A^{-}})}{c({HA})} & \text{Säurekonstante}
\end{array}
\end{align*}

Wenn wir jetzt, wie bei der pH-Wert-Berechnung, den negativ dekadischen Logarithmus auf die Säurekonstante anwenden, erhalten wir den pKS-Wert. Auf dieselbe Weise können wir als Maß für die Stärke einer Base den pKB-Wert angeben. Der Wert ist dabei ein Maß dafür, wie „gerne“ eine Base ein Proton von Wasser aufnimmt.

Mithilfe der pKS- und pKB-Werte können wir nun verschiedene Säuren bzw. Basen bezüglich ihrer Stärke vergleichen.

\begin{array}{|c|c|c|c|}\hline
{pK_\textbf{S}} &
{\textbf{Säure}} &
{\textbf{Korrespondierende Base}} &
{pK_\textbf{B}} \\
\hline
{\text{Vollständige Protonenabgabe}} &
{HCIO_4} &
{CIO_4^{-}} &
{\text{Keine Protonenaufnahme}} \\
\hline
{\text{Vollständige Protonenabgabe}} &
{HI} &
{I^{-}} &
{\text{Keine Protonenaufnahme}} \\
\hline
{\text{Vollständige Protonenabgabe}} &
{HCI} &
{CI^{-}} &
{\text{Keine Protonenaufnahme}} \\
\hline
{\text{Vollständige Protonenabgabe}} &
{H_2SO_4} &
{HSO_4^{-}} &
{\text{Keine Protonenaufnahme}} \\
\hline
-1,74 &
{H_3O^{+}} &
{H_2O} &
15,74 \\
\hline
-1,32 &
{HNO_3} &
{NO_3^{-}} &
15,32 \\
\hline
1,92 &
{HSO_4^{-}} &
{SO_4^{2-}} &
12,08 \\
\hline
2,13 &
{H_3PO_4} &
{H_2PO_4^{-}} &
11,87 \\
\hline
3,14 &
{HF} &
{F^{-}} &
10,86 \\
\hline
3,35 &
{HNO_2} &
{NO_2^{-}} &
10,65 \\
\hline
3,75 &
{HCOOH} &
{HCOO^{-}} &
10,25 \\
\hline
4,75 &
{CH_3COOH} &
{CH_3COO^{-}} &
9,25 \\
\hline
6,52 &
{H_2CO_3} &
{HCO_3^{-}} &
7,48 \\
\hline
6,92 &
{H_2S} &
{HS^{-}} &
7,08 \\
\hline
7,00 &
{HSO_3^{-}} &
{SO_3^{2-}} &
7,00 \\
\hline
7,20 &
{H_2PO_4^{-}} &
{HPO_4^{2-}} &
6,80 \\
\hline
9,25 &
{NH_4^{+}} &
{NH_3} &
4,75 \\
\hline
9,40 &
{HCN} &
{CN^{-}} &
4,60 \\
\hline
10,40 &
{HCO_3^{-}} &
{CO_3^{2-}} &
3,60 \\
\hline
12,36 &
{HPO_4^{2-}} &
{PO_4^{2-}} &
1,64 \\
\hline
13,00 &
{HS^{-}} &
{S^{2-}} &
1,00 \\
\hline
15,74 &
{H_2O} &
{OH^{-}} &
-1,74 \\
\hline
{\text{Keine Protonenabgabe}} &
{C_2H_5OH} &
{CC_2H_5O^{-}} &
{\text{Vollständige Protonenaufnahme}} \\
\hline
{\text{Keine Protonenabgabe}} &
{NH_3} &
{NH_2^{-}} &
{\text{Vollständige Protonenaufnahme}} \\
\hline
{\text{Keine Protonenabgabe}} &
{OH^{-}} &
{O^{2-}} &
{\text{Vollständige Protonenaufnahme}} \\
\hline
{\text{Keine Protonenabgabe}} &
{H_2} &
{H^{-}} &
{\text{Vollständige Protonenaufnahme}} \\
\hline
\end{array}

Die oberen vier Säuren geben ihre Protonen vollständig ab, das heißt es findet eine vollständige Protolyse statt (wir können auch sagen, dass die Säure vollständig dissoziiert). Das Gleichgewicht liegt daher auf der rechten Seite. Je weiter man in der Tabelle nach unten geht, umso größer werden die pKS-Werte und daher umso schwächer die Säuren. In der Tabelle sind auch jeweils die korrespondierendenSäure-Base-Paare angegeben.

Es wird deutlich, dass die korrespondierende Base schwächer ist, je stärker eine Säure ist. Genauso gilt es umgekehrt: Je stärker eine Base ist, desto schwächer ist die korrespondierende Säure.

Zwischen dem pKS-Wert einer Säure und dem pKB-Wert der korrespondierendenBase besteht sogar ein ganz bestimmter Zusammenhang:

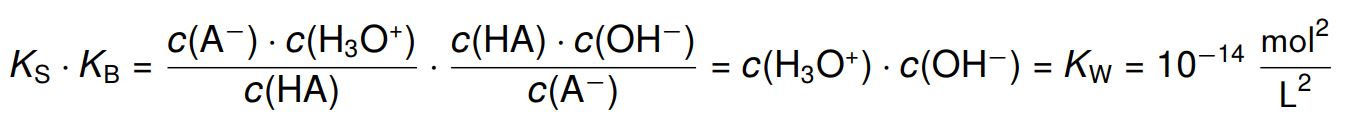
Wenden wir hier den negativ dekadischen Logarithmus an, erhalten wir:

\begin{align*}
pK_\text{S} + pK_\text{B}=14
\end{align*}

Ist also der pKS-Wert einer Säure bekannt, können wir mithilfe der Formel den pKB-Wert der korrespondierenden Base berechnen.

Betrachten wir die Basen in der Tabelle, so können wir sehen, dass die unteren vier Basen sehr stark sind, da diese Protonen vollständig aufnehmen. Das bedeutet, dass alle Base-Teilchen ein Proton aufnehmen.

Jetzt können wir uns fragen, warum das so wichtig ist, ob eine Säure bzw. Base nun stark oder schwach ist. Das wird vor allem dann wichtig, wenn wir den pH-Wert einer Lösung berechnen möchten. Dazu müssen wir die pKS- und die pKB-Werte richtig einordnen können.

Um die Stärke von Säuren und Basen richtig einzuordnen, sind folgende Werte für uns relevant:
\begin{align*}
\begin{array}{ll|ll}
pK_\text{S}<1,5 & starke \ Säure & \quad pK_\text{B}<1,5 & starke \ Base \\
1,5 < pK_\text{S} < 4,75 & mittelstarke \ Säure & \quad 1,5 < pK_\text{B} < 4,75 & mittelstarke \ Base \\ pK_\text{S} > 4,75 & schwache \ Säure & \quad pK_\text{B} > 4,75 & schwache \ Base
\end{array}
\end{align*}

pH-Wert-Berechnung von Säuren und Basen verschiedener Stärken

Starke Säuren

Wenn der pKS-Wert einer Säure kleiner als 1,5 ist, so handelt es sich um eine starke Säure. Dann können wir davon ausgehen, dass die Protolyse nahezu vollständig verläuft. Daher geben alle Säureteilchen ihre Protonen an das Wasser ab, wodurch die Konzentration der Oxoniumionen annähernd die gleiche wie die anfängliche Säurekonzentration ist.

Den pH-Wert können wir also folgendermaßen berechnen:

\begin{align*}
pH =-\lg\left( c({H_3O^{+}}) \right) =-\lg\left( c_0({HA}) \right)
\end{align*}

Schwache Säuren

Bei schwachen Säuren geben nur sehr wenige Säureteilchen ihr Proton an das Wasser ab. Daher ändert sich die Konzentration der Säure durch die Protolyse fast nicht, also c(HA) ≈ c0(HA). Die Konzentration der Oxoniumionen ist hier allerdings genauso groß wie die Konzentration der entstehenden korrespondierenden Base, da für jedes Säureteilchen, das ein Proton abgibt, ein Oxoniumion und ein Teilchen der korrespondierenden Base entstehen, also c(H3O+) = c(A−). Setzt man diese beiden Zusammenhänge in das MWG ein, so erhält man folgende Gleichung:

\begin{align*}
\begin{array}{crcll}
& K_\text{S} & = & \frac{c({A^{-}}) \cdot c({H_3O^{+}})}{c_0({HA})} & \\
\Leftrightarrow & K_\text{S} & = & \frac{c({H_3O^{+}})^2}{c_0({HA})} & |\cdot c_0({HA})
\end{array}
\end{align*}

Um den pH-Wert zu ermitteln, benötigen wir die Konzentration der Oxoniumionen, also lösen wir die Gleichung nach der Konzentration auf:

\begin{align*}
\begin{array}{crcll}
& c({H_3O^{+}})^2 & = & K_\text{S} \cdot c_0({HA}) & |\ \sqrt{ } \\
\Leftrightarrow & c({H_3O^{+}}) & = & \sqrt{K_\text{S} \cdot c_0({HA})} & |\ \text{neg. Logarithmus anwenden} \\
\Rightarrow & \text{pH} & = & -\lg\left (\sqrt{K_\text{S} \cdot c_0({HA})} \right) & \\
& & = & -\frac{1}{2} \cdot \lg \left( K_\text{S} \cdot c_0({HA}) \right) &
\end{array}
\end{align*}

Den pH-Wert können wir also folgendermaßen berechnen:

\begin{align*}
pH =\frac{1}{2} \cdot \left( \text{p}K_\text{S} – lg \ (c_0({HA}) \right))
\end{align*}

Starke Basen

Bei starken Basen können wir quasi die gleiche Formel verwenden wie bei starken Säuren. Achtung: Wenn wir den negativ dekadischen Logarithmus der Anfangskonzentration der Base berechnen, erhalten wir nicht den pH-Wert, sondern den pOH-Wert, da bei der Reaktion einer Base mit Wasser keine Oxoniumionen entstehen, sondern Hydroxidionen. Dies ist aber kein Problem, denn mithilfe des pOH-Wertes können wir den pH-Wert berechnen, nämlich wieder mithilfe des Ionenprodukts des Wassers. Denn daraus ergibt sich folgender Zusammenhang zwischen pH und pOH:
\begin{align*}
\text{pH } + \text{ pOH } = 14
\end{align*}

So lässt sich der pH-Wert bei starken Basen folgendermaßen berechnen:
\begin{align*}
pH =14 + \lg \left( c_0({A^{-}}) \right)
\end{align*}

Schwache Basen

Auch bei schwachen Basen funktioniert die pH-Wert-Berechnung mit derselben Formel wie bei schwachen Säuren, nur, dass wir wieder aufpassen müssen, dass dadurch zunächst der pOH-Wert berechnet wird. Daraus berechnen wir noch den pH-Wert. Hier ergibt sich folgende Formel:

\begin{align*}
pH =14 – \frac{1}{2} \cdot \left( \text{p}K_\text{S} – c_0({HA}) \right)
\end{align*}