Titration

Die Titration ist ein Analyseverfahren, mit dem wir die Konzentration einer Lösung bestimmen können.

Wenn wir also beispielsweise mehrere unbeschriftete Bechergläser mit Salzsäure unterschiedlicher Konzentrationen haben, können wir durch Titration herausfinden, welche Konzentrationen in den jeweiligen Bechergläsern vorliegen.

Eine Titration läuft immer nach dem gleichen Prinzip ab:

Wir haben eine Probelösung in einem Erlenmeyerkolben oder Becherglas, die mit wenigen Tropfen des Indikators versetzt wird. Dann befüllen wir eine Bürette (Glasröhre mit Messstrichen und
Hahn) mit einer Maßlösung (Base mit bekannter Konzentration). Diese Maßlösung geben wir dann tropfenweise zu der Probelösung, bis der Indikator seine Farbe ändert.

Doch wie können wir damit die Konzentration der Probelösung bestimmen?

Beispiel: Betrachten wir 100 mL Salzsäure mit unbekannter Konzentration als Probelösung, zu der tropfenweise Natronlauge der Konzentration NaOH = 0,1 mol=L gegeben wird. Wenn der Indikator umschlägt, können wir das Volumen der zugetropften Natronlauge ablesen. Es wurden V = 40 mL = 0,04 L verbraucht.

Jetzt können wir mit den stöchiometrischen Berechnungen beginnen.

1. Reaktionsgleichung aufstellen

2.Stoffmengenverhältnis aufstellen
\begin{align*}
\frac{n({HCl})}{n({NaOH})} = \frac{1}{1} = 1
\end{align*}

2.Umrechnung der bekannten Größe in die Stoffmenge
\begin{align*}
n({NaOH}) = c({NaOH}) \cdot V({NaOH}) = 0{,}1 \ \frac{{mol}}{{L}} \cdot 0{,}04 \ {L} = 0{,}004 \ {mol} = n({HCl})
\end{align*}

4.Berechnung der Stoffmenge der gesuchten Größe
\begin{align*}
\frac{n({HCl})}{n({NaOH})} = 1 \quad \Rightarrow \quad n({HCl})=n({NaOH})
\end{align*}

5.Gesuchte Größe aus der Stoffmenge berechnen
\begin{align*}
c({HCl}) = \frac{n({HCl})}{V({HCl})} = \frac{0{,}004 \ {mol}}{0{,}1 \ {L}} = 0{,}04 \ \frac{{mol}}{{L}}
\end{align*}

Betrachten wir nun die Titrationskurve.

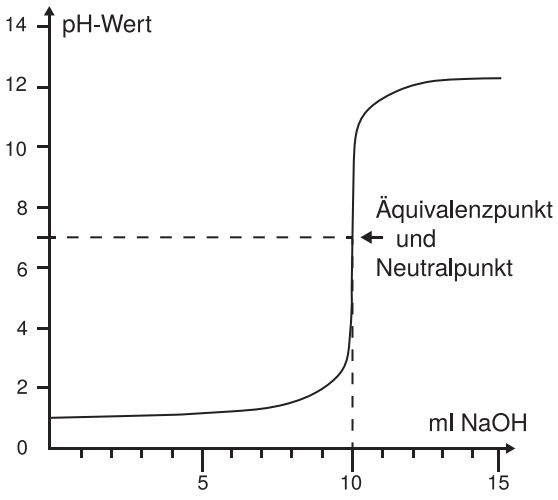
Es wurde Salzsäure (eine starke Säure) mit Natronlauge (eine starke Base) titriert. Der Punkt auf der Titrationskurve, an dem sich die Krümmung ändert, ist der Äquivalenzpunkt. An diesem Punkt wurde eine bestimmte Stoffmenge der Säure mit der entsprechenden Stoffmenge der Base neutralisiert.

Wenn wir eine Säure mit einer gleich starken Base titrieren (pKS ≈ pKB), dann ist der Äquivalenzpunkt gleich dem Neutralpunkt, wobei der Neutralpunkt bei pH = 7 liegt. Sobald unterschiedlich starke Säuren und Basen miteinander titriert werden, liegt der Äquivalenzpunkt nicht im Neutralen. Um den Äquivalenzpunkt können wir einen sehr großen pH-Wert-Sprung beobachten.

Wenn wir statt Salzsäure, Essigsäure (eine schwache Säure) titrieren, sieht die Titrationskure ein wenig anders aus.

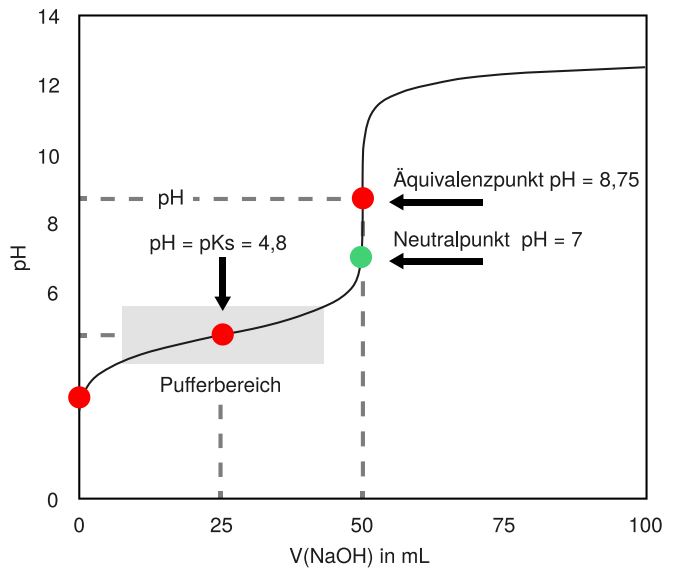
Bei dieser Titration können wir zwei Wendepunkte beobachten. Der Äquivalenzpunkt liegt an dem Wendepunkt, an dem die Kurve am stärksten steigt. Hier sind der Äquivalenzpunkt und der Neutralpunkt nicht identisch. Das liegt daran, dass bei der Säure-Base-Reaktion von Essigsäure mit Natronlauge das basische Acetat-Ion entsteht.

Was hat es denn mit dem zweiten Wendepunkt auf sich?
Hier können wir den pKS-Wert ablesen. Es handelt sich um den Zustand, an dem gleich viele Essigsäuremoleküle wie Acetat-Ionen vorliegen, das heißt, hier hat die Hälfte der Essigsäuremoleküle mit der Base reagiert. Diese Situation haben wir bereits beschrieben, bei den Puffern. Der Bereich um diesen Wendepunkt ist dann der Pufferbereich, was wir auch daran sehen, dass der pH-Wert sich hier nur sehr geringfügig ändert. Der pH-Wert-Sprung um den Äquivalenzpunkt ist auch hier zu sehen, allerdings ist er nicht so extrem wie bei der Titration einer starken Säure.

Nach dem Äquivalenzpunkt sind die Titrationskurven der Titration einer starken Säure und der einer schwachen Säure identisch, da hier die gesamte Säure reagiert hat und nun nur noch die Natronlauge den pH-Wert bestimmt.

\begin{array}{|c|c|}
\hline
\textbf{Titration einer} & \textbf{Eigenschaften} \\
\hline
{\textbf{starken Säure}} &
\text{starker pH-Wert-Sprung um Äquivalenzpunkt} \\
&
\text{Äquivalenzpunkt gleich dem Neutralpunkt} \\
\hline
{{\textbf{schwachen Säure}}} &
\text{pH-Wert-Sprung um den Äquivalenzpunkt nicht so stark} \\
&
\text{Äquivalenzpunkt im basischen} \Rightarrow \text{Äquivalenzpunkt nicht gleich dem Neutralpunkt} \\
&
\text{zweiter Wendepunkt} \Rightarrow pK_\text{S}-Wert \\
\hline
{\textbf{starken Base}} &
\text{starker pH-Wert-Sprung um Äquivalenzpunkt} \\
&
\text{Äquivalenzpunkt gleich dem Neutralpunkt} \\
\hline
{\textbf{schwachen Base}} &
\text{pH-Wert-Sprung um den Äquivalenzpunkt nicht so stark} \\
&
\text{Äquivalenzpunkt im sauren} \Rightarrow \text{Äquivalenzpunkt nicht gleich dem Neutralpunkt} \\
&
\text{zweiter Wendepunkt} \Rightarrow pK_\text{S}-Wert \\
\hline
\end{array}

Ein Spezialfall bleibt. Was passiert bei der Titration einer mehrprotonigen Säure wie beispielsweise Phosphorsäure? \begin{align*} H_3PO_4 \end{align*}

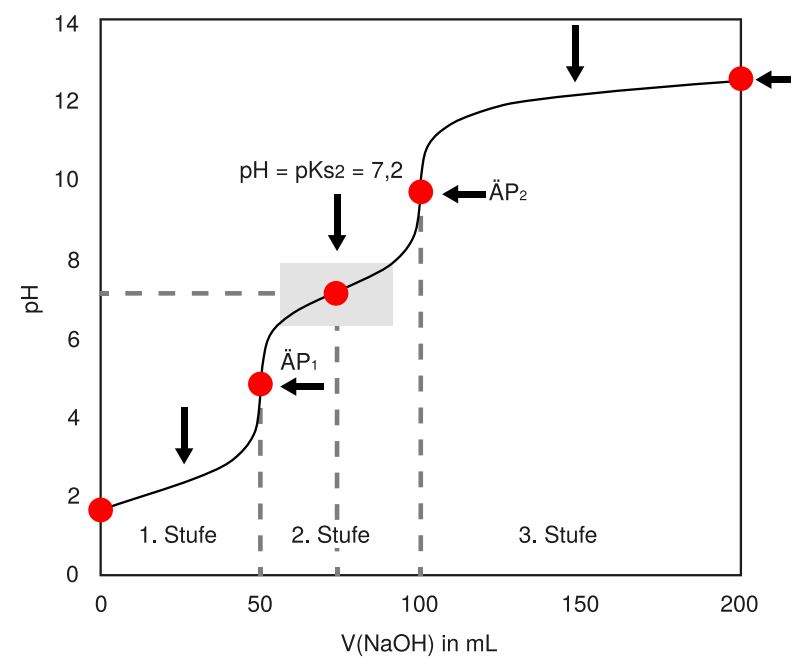
Bei der Titration einer mehrprotonigen Säure liegen uns insgesamt so viele Äquivalenzpunkte wie Protonen vor. Bei der dreiprotonigen Phosphorsäure können wir demnach drei Äquivalenzpunkte (ÄP) ablesen.

Die ersten beiden sind ganz klar zu erkennen, da um die Äquivalenzpunkte wieder pH-Wert-Sprünge zu beobachten sind. Der dritte Äquivalenzpunkt liegt allerdings über einem pH-Wert von 12, weshalb ein pH-Wert-Sprung hier nicht mehr möglich ist. Insgesamt finden wir genauso viele Pufferbereiche wie Protonen, bei der Phosphorsäure entsprechend drei.