Basiswechsel (Vektorraum)

Der Basiswechsel (Basistransformation) gehört zum mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums über einem Körper K. Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren und die Abbildungsmatrizen von linearen Abbildungen. Ein Basiswechsel ist somit ein Spezialfall einer Koordinatentransformation.

Mit Hilfe von Basen kann jeder Vektor im erzeugten Vektorraum eindeutig als Linearkombination der Basisvektoren dargestellt werden. Daher sind sie von weit höherem Interesse als Erzeugendensysteme, die keine Basen sind. Bevor wir uns mit dem Basiswechsel in diesem Artikel auseinandersetzen, klären wir zunächst, welche speziellen Basen/-Bezeichnungen wir kennen müssen.

Inhalt auf dieser Seite

• Standardbasis
• Orthogonalbasis
• Gram-Schmidt-Verfahren
• Orthonormalbasis
• Orthogonalisierungsverfahren
• Orthonormalisierungsverfahren

Standardbasis

Als Standardbasis des $\mathbb{R}^n$ wird die folgende Familie von Vektoren bezeichnet:

\begin{align}
\left(\left(\begin{array}{c}{1}\\{0}\\{\vdots}\\{0}\\{0}\end{array}\right),\left(\begin{array}{c}{0}\\{1}\\{\vdots}\\{0}\\{0}\end{array}\right),\ldots,\left(\begin{array}{c}{0}\\{0}\\{\vdots}\\{1}\\{0}\end{array}\right),\left(\begin{array}{c}{0}\\{0}\\{\vdots}\\{0}\\{1}\end{array}\right)\right)=\left(\overrightarrow{e_1},\overrightarrow{e_2},\ldots,\overrightarrow{e_{n-1}},\overrightarrow{e_n}\right)
\end{align}

Die Basis als Spaltenvektoren in eine Matrix geschrieben, würde das die Einheitsmatrix $E_n$ ergeben.

Orthogonalbasis

Eine Basis wird Orthogonalbasis (OGB) genannt, wenn jeder Vektor aus der Basis zu den anderen Vektoren orthogonal/senkrecht steht (durch Skalarprodukt prüfbar).

\begin{align*}
B=\left(\left(\begin{array}{c}{1}\\{-1}\\{3}\end{array}\right),\left(\begin{array}{c}{-2}\\{13}\\{5}\end{array}\right),\left(\begin{array}{c}{4}\\{1}\\{-1}\end{array}\right)\right) \text{ ist eine OGB des } \mathbb{R}^3, \text{ da }:
\left(\begin{array}{c}{1}\\{-1}\\{3}\end{array}\right) \cdot \left(\begin{array}{c}{-2}\\{13}\\{5}\end{array}\right)=0,\ \left(\begin{array}{c}{1}\\{-1}\\{3}\end{array}\right) \cdot \left(\begin{array}{c}{4}\\{1}\\{-1}\end{array}\right)=0,\ \left(\begin{array}{c}{-2}\\{13}\\{5}\end{array}\right) \cdot \left(\begin{array}{c}{4}\\{1}\\{-1}\end{array}\right)=0
\end{align*}

Die Vektoren sind damit auch eindeutig linear unabhängig! Damit ist $B$ eine OGB des $\mathbb{R}^3$.

Orthonormalbasis

Eine Orthonormalbasis (ONB) hat die folgenden Eigenschaften:

• Sie ist eine Orthogonalbasis
• Alle Vektoren aus der Basis haben die Länge 1

Die Standardbasis ist ebenfalls eine ONB!

\begin{align*}
B=\left(\left(\begin{array}{c}{\frac{1}{\sqrt{5}}}\\{0}\\{\frac{2}{\sqrt{5}}}\end{array}\right),\left(\begin{array}{c}{0}\\{1}\\{0}\end{array}\right),\left(\begin{array}{c}{-\frac{2}{\sqrt{5}}}\\{0}\\{\frac{1}{\sqrt{5}}}\end{array}\right)\right) \text{ ist eine ONB des } \mathbb{R}^3, \text{ da }:
\end{align*}

\begin{align*}
\left(\begin{array}{c}{\frac{1}{\sqrt{5}}}\\{0}\\{\frac{2}{\sqrt{5}}}\end{array}\right){\left(\begin{array}{c}{0}\\{1}\\{0}\end{array}\right)}=0,\ \left(\begin{array}{c}{\frac{1}{\sqrt{5}}}\\{0}\\{\frac{2}{\sqrt{5}}}\end{array}\right)\left(\begin{array}{c}{-\frac{2}{\sqrt{5}}}\\{0}\\{\frac{1}{\sqrt{5}}}\end{array}\right)=0,\ \left(\begin{array}{c}{0}\\{1}\\{0}\end{array}\right)\left(\begin{array}{c}{-\frac{2}{\sqrt{5}}}\\{0}\\{\frac{1}{\sqrt{5}}}\end{array}\right)=0
\end{align*}

Also ist $B$ eine OGB und wegen

\begin{align*}
&\left|\left|\left(\begin{array}{c}{\frac{1}{\sqrt{5}}}\\{0}\\{\frac{2}{\sqrt{5}}}\end{array}\right)\right|\right|=\sqrt{\left(\frac{1}{\sqrt{5}}\right)^2 + \left({0}^2 \right) + \left(\frac{2}{\sqrt{5}}\right)^2} = \sqrt{\frac{1+4}{5}}=1, \quad \left|\left|\left(\begin{array}{c}{0}\\{1}\\{0}\end{array}\right)\right|\right|=1\\
&\left|\left|\left(\begin{array}{c}{-\frac{2}{\sqrt{5}}}\\{0}\\{\frac{1}{\sqrt{5}}}\end{array}\right)\right|\right|=\sqrt{\left(-\frac{2}{\sqrt{5}}\right)^2 + \left({0}^2 \right) + \left(\frac{1}{\sqrt{5}}\right)^2} = \sqrt{\frac{4+1}{5}}=1
\end{align*}

auch eine ONB des $\mathbb{R}^3$.

Gram-Schmidt-Verfahren

Das Gram-Schmidt-Verfahren ist ein Algorithmus um eine beliebige Basis zu einer Orthogonal- oder Orthonormalbasis zu transformieren ohne die lineare Hülle, die von der Basis aufgespannt wird, zu ändern.

Es kursieren zwei mögliche Algorithmen:

• (a) das Gram-Schmidtsche Orthogonalisierungsverfahren
• (b) das Gram-Schmidtsche Orthonormalisierungsverfahren

Wie die Namen schon sagen, erhalten wir mit (a) eine Orthogonal- und mit (b) eine Orthonormalbasis.

Mit (a) lässt sich unserer Meinung nach besser rechnen. Falls du explizit eine Orthonormalbasis mit dem Gram-Schmidt-Verfahren berechnen sollst, kannst du auch erst mit (a) rechnen und nachträglich alle Basisvektoren normieren, anstatt mit (b) zu verfahren.

Lernvideo zum Gram-Schmidt-Verfahren

(a) Orthogonalisierungsverfahren

Wenn eine Basis ($\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3},\ldots,\overrightarrow{a_n}$) gegeben ist und in eine Orthogonalbasis ($\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{u_3},\ldots,\overrightarrow{u_n}$) transformiert werden soll, dann:

\begin{align*}
\overrightarrow{u_1}&:=\overrightarrow{a_1}\\
\overrightarrow{u_2}&=\overrightarrow{a_2}-\frac{{\overrightarrow{a_2}}\bullet{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}\bullet{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}\\[2mm]
\overrightarrow{u_3}&=\overrightarrow{a_3}-\frac{{\overrightarrow{a_3}}\bullet{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}\bullet{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}-\frac{{\overrightarrow{a_3}}\bullet{\overrightarrow{u_2}}}{\overrightarrow{u_2}\bullet\overrightarrow{u_2}}\cdot \overrightarrow{u_2}\\[2mm]
\overrightarrow{u_4}&=\overrightarrow{a_4}-\frac{{\overrightarrow{a_4}}\bullet{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}\bullet{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}-\frac{{\overrightarrow{a_4}}\bullet{\overrightarrow{u_2}}}{\overrightarrow{u_2}\bullet{\overrightarrow{u_2}}}\cdot \overrightarrow{u_2}-\frac{{\overrightarrow{a_4}}\bullet{\overrightarrow{u_3}}}{\overrightarrow{u_3}\bullet{\overrightarrow{u_3}}}\cdot \overrightarrow{u_3}\\[2mm]&\ldots\\[2mm]
\overrightarrow{u_n}&=\overrightarrow{a_n}-\sum_{i=1}^{n-1}\frac{{\overrightarrow{a_n}}\bullet{\overrightarrow{u_i}}}{{\overrightarrow{u_i}}\bullet{\overrightarrow{u_i}}}\cdot \overrightarrow{u_i}
\end{align*}

Teile dieser Formeln solltest du bereits kennen, denn wenn wir uns den Beginn des Algorithmus
\begin{align*}
\overrightarrow{u_1}&:=\overrightarrow{a_1}\\
\overrightarrow{u_2}&=\overrightarrow{a_2}-\frac{{\overrightarrow{a_2}}\bullet{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}\bullet{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}
\end{align*}

ansehen, ist der Teil $\frac{{\overrightarrow{a_2}}{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}$ nichts anderes, als die Projektion von $\overrightarrow{a_2}$ auf $\overrightarrow{u_1}$, also $\overrightarrow{a_2}_{||}$ bzgl. $\overrightarrow{u_1}$.

Damit ist $\overrightarrow{u_2}:=\overrightarrow{a_2}-\frac{{\overrightarrow{a_2}}{\overrightarrow{u_1}}}{{\overrightarrow{u_1}}{\overrightarrow{u_1}}}\cdot \overrightarrow{u_1}$ der senkrechte Teil von $\overrightarrow{a_2}$ bzgl. $\overrightarrow{u_1}$. Das setzt sich dann für $\overrightarrow{u_3},\,\overrightarrow{u_4},\ldots$ fort und wir erhalten eine Orthogonalbasis.

Transformiere die Basis $B=\left(\left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right),\left(\begin{array}{c}{3}\\{3}\\{-1}\end{array}\right),\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)\right)$ in eine Orthogonalbasis.

\begin{align*}
\overrightarrow{u_1}:&=\left(\begin{array}{c}\\{2}\\{0}\\{1}\end{array}\right),\quad {{\overrightarrow{u_1}}{\overrightarrow{u_1}}=5}\\
\overrightarrow{u_2}&=\left(\begin{array}{c}{3}\\{3}\\{-1}\end{array}\right)-\frac{{\left(\begin{array}{c}{3}\\{3}\\{-1}\end{array}\right)}{\left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)}}{5}\cdot \left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)=\left(\begin{array}{c}{3}\\{3}\\{-1}\end{array}\right)-\frac{5}{5}\cdot\left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)=\left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right),\quad {{\overrightarrow{u_2}}{\overrightarrow{u_2}}=14}
\end{align*}

\begin{align*}
\overrightarrow{u_3}&=\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)-\frac{{\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)}{\left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)}}{5}\cdot \left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)-\frac{{\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)}{\left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right)}}{14}\cdot \left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right)\\
&=\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)-\frac{2}{5}\cdot \left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)-\frac{9}{14}\cdot \left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right)=\frac{70}{70}\cdot\left(\begin{array}{c}{2}\\{1}\\{-2}\end{array}\right)-\frac{28}{70}\cdot \left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right)-\frac{45}{70}\cdot \left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right)\\
&=\frac{1}{70}\cdot\left(\begin{array}{c}{140-56-45}\\{70-0-135}\\{-140-28+90}\end{array}\right)=\frac{1}{70}\left(\begin{array}{c}{39}\\{-65}\\{-78}\end{array}\right)=\left(\begin{array}{c}{\frac{39}{70}}\\{-\frac{13}{14}}\\{-\frac{39}{35}}\end{array}\right)
\end{align*}

Orthogonalbasis $\left(\left(\begin{array}{c}{2}\\{0}\\{1}\end{array}\right),\left(\begin{array}{c}{1}\\{3}\\{-2}\end{array}\right),\left(\begin{array}{c}{39}{70}\\{-\frac{13}{14}}\\{-\frac{39}{35}}\end{array}\right)\right)$ gefunden.

Orthonormalisierungsverfahren

Wenn eine Basis ($\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3},\ldots,\overrightarrow{a_n}$) gegeben ist und in eine Orthonormalbasis ($\overrightarrow{u_1},\overrightarrow{u_2},\overrightarrow{u_3},\ldots,\overrightarrow{u_n}$) transformiert werden soll, dann:
\begin{align*}
\overrightarrow{u^*_1}&:=\overrightarrow{a_1},\quad \overrightarrow{u_1}=\frac{\overrightarrow{u^*_1}}{\left|\left|{\overrightarrow{u^*_1}}\right|\right|}\\
\overrightarrow{u^*_2}&=\overrightarrow{a_2}-\left({\overrightarrow{a_2}}\bullet{\overrightarrow{u_1}}\right)\cdot \overrightarrow{u_1},\quad \overrightarrow{u_2}=\frac{\overrightarrow{u^*_2}}{\left|\left|{\overrightarrow{u^*_2}}\right|\right|}\\
\overrightarrow{u^*_3}&=\overrightarrow{a_3}-\left({\overrightarrow{a_3}}\bullet{\overrightarrow{u_1}}\right)\cdot \overrightarrow{u_1}-\left({\overrightarrow{a_3}}\bullet{\overrightarrow{u_2}}\right)\cdot \overrightarrow{u_2},\quad \overrightarrow{u_3}=\frac{\overrightarrow{u^*_3}}
{\left|\left|{\overrightarrow{u^*_3}}\right|\right|}\\
\overrightarrow{u^*_4}&=\overrightarrow{a_4}-\left({\overrightarrow{a_4}}\bullet{\overrightarrow{u_1}}\right)\cdot \overrightarrow{u_1}-\left({\overrightarrow{a_4}}\bullet{\overrightarrow{u_2}}\right)\cdot \overrightarrow{u_2}-\left({\overrightarrow{a_4}}\bullet{\overrightarrow{u_3}}\right)\cdot
\overrightarrow{u_3},\quad \overrightarrow{u_4}=\frac{\overrightarrow{u^*_4}}{\left|\left|{\overrightarrow{u^*_4}}\right|\right|}\\
&\ldots\\
\overrightarrow{u^*_n}&=\overrightarrow{a_n}-\sum_{i=1}^{n-1}{\left({\overrightarrow{a_n}}{\overrightarrow{u_i}}\right)\cdot\overrightarrow{u_i}},\quad \overrightarrow{u_n}=\frac{\overrightarrow{u^*_n}}{\left|\left|{\overrightarrow{u^*_n}}\right|\right|}
\end{align*}

Beispiel

Finde eine Orthonormalbasis zu dem UVR, der der Ebene $E:\ \overrightarrow{x}=\lambda\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)+\mu\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right),\ \lambda,\mu\in\mathbb{R}$ entspricht.

Eine Basis zu $E$ ist durch $\left(\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right),\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)\right)$ gegeben.

Verfahren (a):
\begin{align*}
\overrightarrow{u_1}:&= \left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right),\quad {{\overrightarrow{u_1}}\bullet{\overrightarrow{u_1}}=36+3+9=48}\\
\overrightarrow{u_2}&= \left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)-\frac{{\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)}\bullet\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)}{48}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)=\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)-\frac{48}{48}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)=\left(\begin{array}{c}{0}\\{\sqrt{3}}\\{1}\end{array}\right)
\end{align*}

Normieren:
\begin{align*}
\frac{\overrightarrow{u_1}}{\left|\left|{\overrightarrow{u_1}}\right|\right|}=\frac{1}{\sqrt{48}}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right),\qquad\frac{\overrightarrow{u_2}}{{\overrightarrow{u_2}}}=\frac{1}{2}\cdot\left(\begin{array}{c}{0}\\{\sqrt{3}}\\{1}\end{array}\right)
\end{align*}

Eine Orthonormalbasis zu $E$ ist also $\left(\frac{1}{\sqrt{48}}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right),\frac{1}{2}\cdot\left(\begin{array}{c}{0}\\{\sqrt{3}}\\{1}\end{array}\right)\right)$

Verfahren (b):
\begin{align*}
\overrightarrow{u^*_1}:&=\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right),\quad \overrightarrow{u_1}=\frac{\overrightarrow{u^*_1}}{\left|\left|{\overrightarrow{u^*_1}}\right|\right|}=\frac{1}{48}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)\\
\overrightarrow{u^*_2}&=\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)-\left({\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)}\bullet{\frac{1}{\sqrt{48}}\cdot\left(\begin{array}{c}{6}{-\sqrt{3}}\\{3}\end{array}\right)}\right)\cdot\frac{1}{\sqrt{48}}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)\\
&=\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)-\frac{1}{\sqrt{48}}\cdot 48\cdot\frac{1}{\sqrt{48}}\cdot\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)=\left(\begin{array}{c}{6}\\{0}\\{4}\end{array}\right)-\left(\begin{array}{c}{6}\\{-\sqrt{3}}\\{3}\end{array}\right)=\left(\begin{array}{c}{0}\\{\sqrt{3}}\\{1}\end{array}\right)\\
&\overrightarrow{u_2}=\frac{\overrightarrow{u^*_2}}{\left|\left|{\overrightarrow{u^*_2}}\right|\right|}=\frac{1}{2}\cdot\left(\begin{array}{c}{0}\\{\sqrt{3}}\\{1}\end{array}\right)
\end{align*}

Basiswechsel

Wenn wir die Lage von Punkten beschreiben, benötigen wir dafür Koordinaten. Diese beziehen sich allerdings immer auf eine bestimmte Basis. Normalerweise ist das die Standardbasis (Koordinaten ablesbar an der $x$-, $y$– und $z$-Achse). Wollen wir die Lage eines Punktes mit einer anderen Basis beschreiben, so führen wir einen Basiswechsel durch.

Komfortabel wäre es nun, wenn wir eine Matrix hätten, mit welcher wir die Koordinaten eines Punktes bzgl. einer Basis $B$ in eine andere Basis $B^\prime$ überführen könnten. Diese Matrix wird Basiswechselmatrix oder Transformationsmatrix genannt und für gewöhnlich mit ${T}^B_{B^‘}$ bezeichnet.

Wenn nun mit (allgemein) $B=(\overrightarrow{b_1},\overrightarrow{b_2},\overrightarrow{b_3},\ldots)$ und $B^\prime=(\overrightarrow{b^\prime_1},\overrightarrow{b^\prime_2},\overrightarrow{b^\prime_3},\ldots)$ zwei verschiedene Basen des selben Vektorraums gegeben sind, gilt für einen beliebigen Punkt $P=(p_1,p_2,p_3,\ldots)$ bzw. $\overrightarrow{0P}={(p_1,\ p_2,\ p_3,\ \ldots)}$:

\begin{align*}
\text{In Standardbasis:}\quad& p_1\cdot\overrightarrow{e_1}+p_2\cdot\overrightarrow{e_2}+p_3\cdot\overrightarrow{e_3}+\ldots=&\overrightarrow{0P}\\
\text{In Basis $B$:}\quad& x_{b_1}\cdot\overrightarrow{b_1}+x_{b_2}\cdot\overrightarrow{b_2}+x_{b_3}\cdot\overrightarrow{b_3}+\ldots=&\overrightarrow{0P}\\
\text{In Basis $B^\prime$:}\quad& x_{b^\prime_1}\cdot\overrightarrow{b^\prime_1}+x_{b^\prime_2}\cdot\overrightarrow{b^\prime_2}+x_{b^\prime_3}\cdot\overrightarrow{b^\prime_3}+\ldots=&\overrightarrow{0P}
\end{align*}

Die $p_{\ldots}$ sind die Koordinaten von $P$ bzgl. der Standardbasis, $x_{b_{\ldots}}$ die Koordinaten bzgl. Basis $B$ und $x_{b^\prime_{\ldots}}$ bzgl. Basis $B^\prime$. Wenn jetzt die Koordinaten von $P$ bzgl. Basis $B$ bekannt/gegeben sind, können wir dies nutzen:

\begin{alignat}{2}
&& x_{b_1}\cdot\overrightarrow{b_1}+x_{b_2}\cdot\overrightarrow{b_2}+x_{b_3}\cdot\overrightarrow{b_3}+\ldots&=x_{b^\prime_1}\cdot\overrightarrow{b^\prime_1}+x_{b^\prime_2}\cdot\overrightarrow{b^\prime_2}+x_{b^\prime_3}\cdot\overrightarrow{b^\prime_3}+\ldots\notag
\end{alignat}

In Matrix-Vektor-Schreibweise:
\begin{alignat}{2}
&& \underbrace{(\overrightarrow{b_1}\overrightarrow{b_2}\overrightarrow{b_3}\ldots)}_{\text{Matrix}}\left(\begin{array}{c}{x_{b_1}}\\{x_{b_2}}\\{x_{b_3}}\\{\vdots}\end{array}\right)&=\underbrace{(\overrightarrow{b^\prime_1}\overrightarrow{b^\prime_2}\overrightarrow{b^\prime_3}\ldots)}_{\text{Matrix}}\left(\begin{array}{c}{x_{b^\prime_1}}\\{x_{b^\prime_2}}\\{x_{b^\prime_3}}\\{\vdots}\end{array}\right) \ \Bigl|\Bigr.\ \text{Inverse von links}\notag\\[2mm]
\Leftrightarrow \quad&& \underbrace{{(\overrightarrow{b^\prime_1}\overrightarrow{b^\prime_2}\overrightarrow{b^\prime_3}\ldots)}(\overrightarrow{b_1}\overrightarrow{b_2}\overrightarrow{b_3}\ldots)}_{=\,{T}^B_{B^\prime}}\left(\begin{array}{c}{x_{b_1}}\\{x_{b_2}}\\{x_{b_3}}\\{\vdots}\end{array}\right)&=\left(\begin{array}{c}{x_{b^\prime_1}}\\{x_{b^\prime_2}}\\{x_{b^\prime_3}}\\{\vdots}\end{array}\right)\\
\Leftrightarrow \quad&& {T}^B_{B^\prime}\left(\begin{array}{c}{x_{b_1}}\\{x_{b_2}}\\{x_{b_3}}\\{\vdots}\end{array}\right)&=\left(\begin{array}{c}{x_{b^\prime_1}}\\{x_{b^\prime_2}}\\{x_{b^\prime_3}}\\{\vdots}\end{array}\right)\quad\text{(für die Berechnung der neuen Koordinaten)}\notag
\end{alignat}

Für die Transformationsmatrix von Basis $B$ nach Basis $B^\prime$ gilt also:
\begin{alignat}{2}
&& {T}^B_{B^\prime}&={(\overrightarrow{b^\prime_1}\overrightarrow{b^\prime_2}\overrightarrow{b^\prime_3}\ldots)}(\overrightarrow{b_1}\overrightarrow{b_2}\overrightarrow{b_3}\ldots)\notag\\%
\Leftrightarrow\quad&& (\overrightarrow{b^\prime_1}\overrightarrow{b^\prime_2}\overrightarrow{b^\prime_3}\ldots)\cdot{T}^B_{B^\prime}&=(\overrightarrow{b_1}\overrightarrow{b_2}\overrightarrow{b_3}\ldots)
\end{alignat}
Dies sind nun mehrere LGS, welche wir zusammen lösen können:

An dieser Stelle nochmal ein Grundlagenvideo zum Basiswechsel

Berechnen der Transformationsmatrix ${T}^B_{B^\prime}$ (Basiswechsel von Basis $\pmb{B}$ nach $\pmb{B^\prime}$}

Basen $B=(\overrightarrow{b_1},\overrightarrow{b_2},\overrightarrow{b_3},\ldots)$ und $B^\prime=(\overrightarrow{b^\prime_1},\overrightarrow{b^\prime_2},\overrightarrow{b^\prime_3},\ldots)$ gegeben.

1. Matrizen ${B}=(\overrightarrow{b_1}\overrightarrow{b_2}\overrightarrow{b_3}\ldots)$ und ${B}^\prime=(\overrightarrow{b^\prime_1}\overrightarrow{b^\prime_2}\overrightarrow{b^\prime_3}\ldots)$ mit den jew. Basisvektoren als Spalten aufstellen
2. LGS aufstellen mit Kurzschreibweise $({B}^\prime|{B})$

Links steht die neue Basis — Rechts steht die alte Basis!

1. Durch elementare Zeilenumformungen die linke Seite auf die Einheitsmatrix bringen (wie beim Berechnen einer Inversen)
2. LGS ist nun in Form $({E}|{T}^B_{B^\prime})$ und die Transformationsmatrix kann abgelesen werden

Beispiel

Wie lauten die Koordinaten des Punktes $P_B=(1,2,3)$ ($P_B$ bzgl. Basis $B$) bzgl. Basis $B^\prime$ mit

\begin{align*}
B=\left(\left(\begin{array}{c}{1}\\{0}\\{1}\end{array}\right),\left(\begin{array}{c}{3}\\{1}\\{0}\end{array}\right),\left(\begin{array}{c}{-1}\\{1}\\{1}\end{array}\right)\right)\quad\text{und}\quad B^\prime=\left(\left(\begin{array}{c}{1}\\{1}\\{1}\end{array}\right),\left(\begin{array}{c}{0}\\{1}\\{2}\end{array}\right),\left(\begin{array}{c}{1}\\{0}\\{1}\end{array}\right)\right)
\end{align*}

Matrizen aus den Basisvektoren:

\begin{align*}
{B}=\left(
\begin{matrix} % 3×3
1 & 3 & -1 \\
0 & 1 & 1 \\
1 & 0 & 1
\end{matrix}\right),
\quad{B}^\prime=\left(\begin{matrix} % 3×3
1 & 0 & 1 \\
1 & 1 & 0 \\
1 & 2 & 1
\end{matrix}\right)
\end{align*}

Transformationsmatrix ${T}^B_{B^\prime}$ bestimmen. Löse ${B}^\prime{T}^B_{B^\prime}={B}\rightarrow({B}^\prime|{B})$:

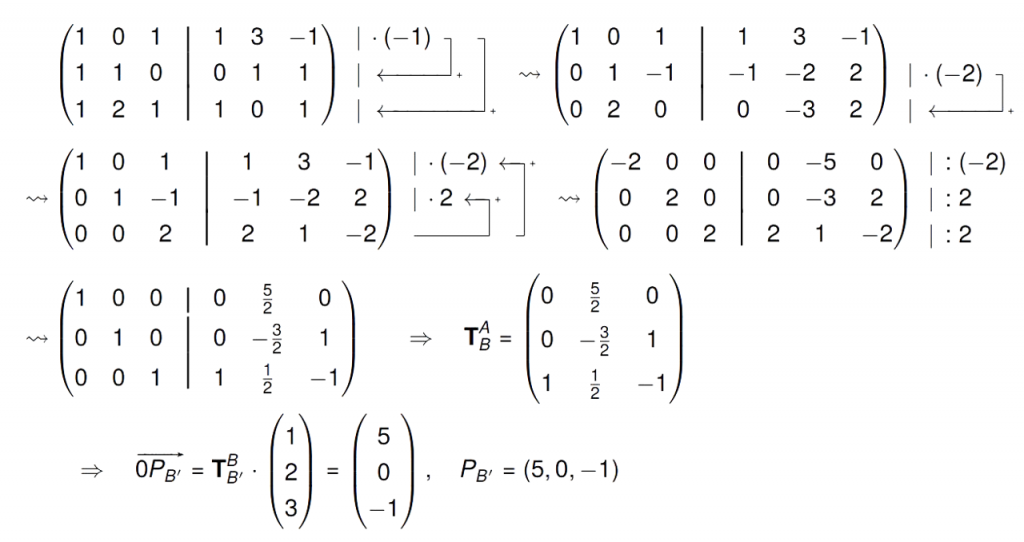
Zur Probe:
\begin{align*}
\text{Aus Basis }B\text{ in Standardbasis:}\quad&1\cdot\left(\begin{array}{c}{1}\\{0}\\{1}\end{array}\right)+2\cdot\left(\begin{array}{c}{3}\\{1}\\{0}\end{array}\right)+3\cdot\left(\begin{array}{c}{-1}\\{1}\\{1}\end{array}\right)=\left(\begin{array}{c}{4}\\{5}\\{4}\end{array}\right)\\
\text{Aus Basis }B^\prime\text{ in Standardbasis:}\quad&5\cdot\left(\begin{array}{c}{1}\\{1}\\{1}\end{array}\right)+0\cdot\left(\begin{array}{c}{0}\\{1}\\{2}\end{array}\right)-1\cdot\left(\begin{array}{c}{1}\\{0}\\{1}\end{array}\right)=\left(\begin{array}{c}{4}\\{5}\\{4}\end{array}\right)
\end{align*}

Bzgl. der Standardbasis hat der Punkt $P$ also die Koordinaten P=(4,5,4).