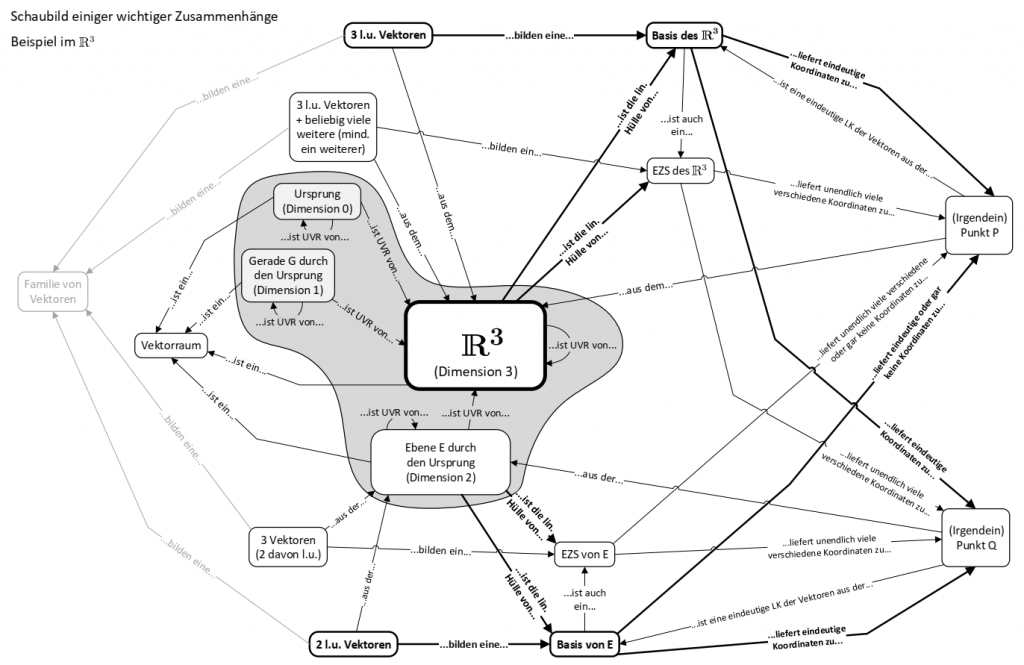
Vektorraum

Ein Vektorraum ist eine algebraische Struktur (eine Menge mit Verknüpfungsgebilden). Die Elemente eines Vektorraums werden Vektoren genannt. Sie können beliebig addiert oder mit Zahlen multipliziert werden, wobei das Ergebnis ein Vektor desselben Vektorraums ist.

Inhalt auf dieser Seite

• Familie von Vektoren
• Linearkombination
• Untervektorraum
• Nullvektorraum
• Schaubild Vektorräume

Zur Einführung in das Thema Vektorraum haben wir an dieser Stelle ein passendes Lernvideo bereitgestellt:

Definition eines Vektorraums

Ein Vektorraum sieht abstrakt notiert wie folgt aus:

\begin{align}
(V,\oplus,\odot)
\end{align}

$V$ ist eine Menge. $\oplus$ und $\odot$ sind Verknüfpungen.

Es existiert ein Vektorraum $(V,\oplus,\odot)$ über $\mathbb{R}$, mit:

• Menge $V=\left\{\ldots\right\}$
• Innerer Verknüpfung $\oplus: V\times V \rightarrow V$ (Vektoraddition)
  $\text{d.h. es gilt:}\quad \forall x,y\in V: x\oplus y\in V$
• Äußerer Verknüpfung $\odot: \mathbb{R}\times V \rightarrow V$ (skalare Multiplikation)
  $\text{d.h. es gilt:}\quad \forall x\in V\ \forall \alpha\in\mathbb{R}: \alpha\odot x\in V$

Daraus resultierend sagen wir: $(V,\oplus,\odot)$ ([/latex]oder: $(V,\oplus,\odot)$) ist Vektorraum über $\mathbb{R}\ldots$, wenn die 8 Vektorraumaxiome gelten:

Axiome der Vektoraddition $\oplus$

1. $\forall x,y\in V: x\oplus y=y\oplus x \qquad\qquad\qquad \ \ \ \ \ \ $(Kommutativgesetz)
2. $\forall x,y,z\in V: x\oplus (y\oplus z)=(x\oplus y)\oplus z \ \ \ \ \ \ \ $(Assoziativgesetz)
3. $\exists 0\in V\ \forall x\in V: x\oplus 0 = x\qquad\qquad\qquad \ \ \ $(Existenz eines neutralen Elements)
4. $\forall x\in V\ \exists -x\in V: x\oplus -x = 0\qquad\qquad \ \ \ $(Existenz eines inversen Elements)

Axiome der skalaren Multiplikation $\odot$

1. $\forall\alpha,\beta\in\mathbb{R}\ \forall x\in V: (\alpha+\beta)\odot x=(\alpha\odot x)\oplus(\beta\odot x)\qquad$(Skalares Distributivgesetz)
2. $\forall\alpha\in\mathbb{R}\ \forall x,y\in V: \alpha\odot(x\oplus y)=(\alpha\odot x)\oplus(\alpha\odot y)\qquad \ $(Vektorielles Distributivgesetz)
3. $\forall \alpha,\beta\in\mathbb{R}\ \forall x\in V: (\alpha\cdot\beta)\odot x=\alpha\odot(\beta\odot x)\qquad\qquad \ \ \ \ $(Assoziativgesetz für Skalare)
4. $1\in\mathbb{R}\ \forall x\in V: 1\odot x=x\qquad\qquad\qquad \ \ \ \qquad$(Neutrales Element bezüglich der skalaren Multiplikation)

• $\mathbb{R}$, $\mathbb{R}^2$, $\mathbb{R}^3,\ldots,\mathbb{R}^n$ sind Vektorräume.
• Die Menge aller Polynome bis zum Grad $n$ ist ein Vektorraum.

Beispiel mit $V=\mathbb{R}^2$

$\oplus$ entspricht hier der Vektoraddition (Komponentenweise):

$\odot$ entspricht hier der Skalarmultiplikation:

1. 1. $\forall x,y\in V: x\oplus y=y\oplus x$. Also: $\forall \ \overrightarrow{x}, \ \overrightarrow{y}\in\mathbb{R}^2$

\begin{align*}
&\overrightarrow{x}\oplus\overrightarrow{y}=\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{y_1}\\{y_2}\end{array}\right)=\left(\begin{array}{c} {x_1+y_1}\\{x_2+y_2}\end{array}\right) \\ \\
&=\left(\begin{array}{c}{y_1+x_1}\\{y_2+x_2}\end{array}\right)=\left(\begin{array}{c}{y_1}\\{y_2}\end{array}\right)\oplus\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)=\overrightarrow{y}\oplus\overrightarrow{x}
\end{align*}

1. $\forall x,y,z\in V: x\oplus (y\oplus z)=(x\oplus y)\oplus z.\quad \text{Also}: \forall \overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\in\mathbb{R}^2$:\begin{align*}
   &\overrightarrow{x}\oplus (\overrightarrow{y}\oplus \overrightarrow{z})=\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{y_1}\\{y_2}\end{array}\right)\oplus\left(\begin{array}{c}{z_1}\\{z_2}\end{array}\right)=\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{y_1+z_1}\\{y_2+z_2}\end{array}\right)\\ \\
   &=\left(\begin{array}{c}{x_1+y_1+z_1}\\{x_2+y_2+z_2}\end{array}\right)=\left(\begin{array}{c}{x_1+y_1}\\{x_2+y_2}\end{array}\right)\oplus\left(\begin{array}{c}{z_1}\\{z_2}\end{array}\right)=\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{y_1}\\{y_2}\end{array}\right)\oplus\left(\begin{array}{c}{z_1}{z_2}\end{array}\right)=( \overrightarrow{x}\oplus\ \overrightarrow{y} )\oplus \overrightarrow{z}
   \end{align*}
2. $\exists 0\in V\ \forall x\in V: x\oplus 0 = x.\quad \text{Also: }\exists \overrightarrow{0}\in\mathbb{R}^2\ \forall \overrightarrow{x}\in\mathbb{R}^2: \overrightarrow{x}\oplus\overrightarrow{0} = \overrightarrow{x}$:\begin{align*}
   \exists \left(\begin{array}{c}{0}\\{0}\end{array}\right)\in\mathbb{R}^2 \forall \left(\begin{array}{c}{x_1} \\ {x_2}\end{array}\right)\in\mathbb{R}^2:)\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{0}\\{0}\end{array}\right)=\left(\begin{array}{c}{x_1+0}\\{x_2+0}\end{array}\right) = \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)
   \end{align*}
3. $\forall x\in V\ \exists -x\in V: x\oplus -x = 0. \quad \text{Also: }\forall \overrightarrow{x}\in\mathbb{R}^2\ \exists -\overrightarrow{x}\in\mathbb{R}^2: \overrightarrow{x}\oplus -\overrightarrow{x} = \overrightarrow{0}$:\begin{align*}
   \forall \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\in\mathbb{R}^2\ \exists \left(\begin{array}{c}{-x_1}\\{-x_2}\end{array}\right)\in\mathbb{R}^2: \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus\left(\begin{array}{c}{-x_1}\\{-x_2}\end{array}\right)=\left(\begin{array}{c}{x_1+(-x_1)}\\{x_2+(-x_2)}\end{array}\right) = \left(\begin{array}{c}{0}\\{0}\end{array}\right)
   \end{align*}
4. $\forall\alpha,\beta\in\mathbb{R} \forall x\in V: (\alpha+\beta)\odot x=(\alpha\odot x)\oplus(\beta\odot x)$.Also: $\forall\alpha,\beta\in\mathbb{R}\ \forall \overrightarrow{x}\in\mathbb{R}^2: (\alpha+\beta)\odot \overrightarrow{x}=(\alpha\odot \overrightarrow{x})\oplus(\beta\odot \overrightarrow{x})$:\begin{align*}
   &(\alpha+\beta)\odot\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)=\left(\begin{array}{c}(\alpha+\beta)\cdot x_1\\(\alpha+\beta)\cdot x_2\end{array}\right)=\left(\begin{array}{c}{\alpha\cdot x_1+\beta\cdot x_1}\\{\alpha\cdot x_2+\beta\cdot x_2}\end{array}\right) \\ \\
   &=\left(\begin{array}{c}{\alpha\cdot x_1}\\{\alpha\cdot x_2}\end{array}\right)\oplus\left(\begin{array}{c}{\beta\cdot x_1}\\{\beta\cdot x_2}\end{array}\right)=\left(\alpha\odot\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\right)\oplus\left(\beta\odot\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\right)
   \end{align*}
5. $\forall\alpha\in\mathbb{R}\ \forall x,y\in V: \alpha\odot(x\oplus y)=(\alpha\odot x)\oplus(\alpha\odot y).$Also: $\forall\alpha\in\mathbb{R}\ \forall \overrightarrow{x},\overrightarrow{x}\in \mathbb{R}^2: \alpha\odot(\overrightarrow{x}\oplus \overrightarrow{y})=(\alpha\odot \overrightarrow{x})\oplus(\alpha\odot \overrightarrow{y})$:\begin{align*}
   &\alpha\odot\left(\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\oplus
   \left(\begin{array}{c}{y_1}\\{y_2}\end{array}
   \right)\right)=\alpha\odot\left(
   \begin{array}{c}{x_1+y_1}\\{x_2+y_2}\end{array}\right)
   =\left(\begin{array}{c}{\alpha\cdot(x_1+y_1)}\\{\alpha\cdot(x_2+y_2)}\end{array}
   \right)=\left(\begin{array}{c}{\alpha\cdot x_1+\alpha\cdot y_1}\\{\alpha\cdot x_2+\alpha\cdot y_2}\end{array}\right)\\ \\
   &=\left(\begin{array}{c}{\alpha\cdot x_1}\\{\alpha\cdot x_2}\end{array}
   \right)\oplus\left(\begin{array}{c}{\alpha\cdot y_1}\\{\alpha\cdot y_2}
   \end{array}\right)=\left(\alpha\odot\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\right)\oplus
   \left(\alpha\odot\left(\begin{array}{c}{y_1}\\{y_2}\end{array}\right)\right)
   \end{align*}
6. $\forall \alpha,\beta\in\mathbb{R}\ \forall x\in V: (\alpha\cdot\beta)\odot x=\alpha\odot(\beta\odot x).$Also: $\forall \alpha,\beta\in\mathbb{R}\ \forall \overrightarrow{x}\in \mathbb{R}^2: (\alpha\cdot\beta)\odot \overrightarrow{x}=\alpha\odot(\beta\odot \overrightarrow{x}):$\begin{align*}
   &(\alpha\cdot\beta)\odot \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)=\left(\begin{array}{c}{(\alpha\cdot\beta)\cdot x_1}\\{(\alpha\cdot\beta)\cdot x_2}\end{array}\right)=\left(\begin{array}{c}{\alpha\cdot(\beta\cdot x_1)}\\{\alpha\cdot(\beta\cdot x_2)}\end{array}\right)\\ \\
   &=\alpha\odot\left(\begin{array}{c}{\beta\cdot x_1}\\{\beta\cdot x_2}\end{array}\right)=\alpha\odot\left(\beta\odot\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\right)
   \end{align*}
7. $1\in\mathbb{R}\ \forall x\in V: 1\odot x=x.\quad \text{Also: } 1\in\mathbb{R}\ \forall \overrightarrow{x}\in \mathbb{R}^2: 1\odot \overrightarrow{x}=\overrightarrow{x}$:\begin{align*}
   1\in\mathbb{R}\ \forall \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)\in \mathbb{R}^2: 1\odot \left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)=\left(\begin{array}{c}{1\cdot x_1}\\{1\cdot x_2}\end{array}\right)=\left(\begin{array}{c}{x_1}\\{x_2}\end{array}\right)
   \end{align*}

Familie von Vektoren

Eine Familie von Vektoren ist ähnlich einer Menge von Vektoren, sprich eine Auflistung von Vektoren. Der einzige Unterschied liegt hier in der mathematischen Definition einer Menge (in welcher exakt gleiche Objekte gestrichen werden dürfen, ohne die Menge zu verändern) zu der einer Familie (in welcher nichts herausgestrichen werden darf, ganz gleich ob ein Vektor mehrfach vorhanden ist).

Beispiel aus Vektorraum $\mathbb{R}^3$: Vektor $(1,2,3)^T$ kommt doppelt vor:

\begin{align*}
\text{Menge }&M=\left\{\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right),\left(\begin{array}{c}{0}\\{2}\\{7}\end{array}\right),\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right)\right\}=\left\{\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right),\left(\begin{array}{c}{0}\\{2}\\{7}\end{array}\right)\right\}\\
\text{Familie }&F=\left(\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right),\left(\begin{array}{c}{0}\\{2}\\{7}\end{array}\right),\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right)\right)\neq\left(\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right),\left(\begin{array}{c}{0}\\{2}\\{7}\end{array}\right)\right)
\end{align*}

Die Menge bleibt bei Streichung einer dieser beiden Vektoren aus mathematischer Sicht gleich. Die Familie verändert sich!

Linearkombination

Eine Linearkombination von Vektoren ist die Summe aus beliebigen Skalierungen dieser Vektoren:

\begin{align*}
& 2\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+3\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)=\left(\begin{array}{c}{-2}\\{-2}\\{-3}\end{array}\right)
\end{align*}

Der Vektor $(-2,-2,-3)^T$ ist eine LK von $(2,-1,3)^T$ und $(-2,0,-3)^T$. Wir können auch sagen, dass sich der Vektor $(-2,-2,-3)^T$ durch die beiden Vektoren $(2,-1,3)^T$ und $(-2,0,-3)^T$ darstellen lässt, indem $(2,-1,3)^T$ um das zweifache und $(-2,0,-3)^T$ um das dreifache verlängert wird.

Eine wichtige, andere Schreibweise ist, die LK als Matrix$\cdot$Vektor schreiben zu können:

\begin{align*}
& 2\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+3\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)=\begin{pmatrix} % 3×3
2 & -2 \\
-1 & 0 \\
3 & -3
\end{pmatrix}\left(\begin{array}{c}2\\3\end{array}\right)=\left(\begin{array}{c}{-2}\\{-2}\\{-3}\end{array}\right)
\end{align*}

Das stellt im Prinzip ein gelöstes inhomogenes LGS dar.

Untervektorraum

Ein Untervektorraum (auch Unterraum genannt) $U$ ist eine Teilmenge eines Vektorraums $V$, wobei $U$ selbst wieder ein Vektorraum ist.

Es ist $U\subseteq V$ bekannt. Alle Elemente aus $U$ sind also auch Elemente aus $V$ und $V$ unterliegt den 8 Vektorraumaxiomen. Es genügt daher, folgende 3 Bedingungen zu prüfen, wenn gefragt ist, ob $U$ ein Untervektorraum von $V$ ist:

1. $U\neq\{\}\quad(\text{Gilt also: }\overrightarrow{0}\in U?)$
2. $\forall x,y\in U:\quad x\oplus y\in U$
3. $\forall x\in U\ \forall\lambda\in\mathbb{R}:\quad \lambda\odot x\in U$

Diese drei Punkte können wir theoretisch zusammenfassen durch den Satz:

Jede mögliche LK von Elementen aus der nicht-leeren Menge $U$ muss wieder in $U$ liegen.

1. Geraden im $\mathbb{R}^2$ (bzw. $\mathbb{R}^3$) durch den Ursprung sind UVR des $\mathbb{R}^2$ (bzw. $\mathbb{R}^3$)
2. Ebenen (im $\mathbb{R}^3$) durch den Ursprung sind UVR des $\mathbb{R}^3$
3. $\mathbb{R}$ (bzw. $\mathbb{R}^2$ oder $\mathbb{R}^3$) selbst sind UVR des $\mathbb{R}$ (bzw. $\mathbb{R}^2$ oder $\mathbb{R}^3$)

Beispiel

$U:=\left\{\overrightarrow{x}\in\mathbb{R}^3\ \Bigl|\Bigr.\ 3x_1+2x_2-x_3=0\right\}$ ist UVR des $\mathbb{R}^3$, da:

\begin{align*}
1)\quad& \overrightarrow{0}\in U \quad 3\cdot 0+2\cdot 0-0=0\quad\text{korrekt}\\ \\
2)\quad& \text{Sei }(x_1,x_2,x_3)^T ,(y_1,y_2,y_3)^T\in U\ |\text{ dann gilt:} \\ \\
\Leftrightarrow\quad& 3x_1+2x_2-x_3=0\ \wedge\ 3y_1+2y_2-y_3=0\ | \text{ addieren} \\ \\
\Rightarrow\quad& 3x_1+2x_2-x_3+3y_1+2y_2-y_3=0+0\ | \text{ sortieren} \\ \\
\Leftrightarrow\quad& 3(x_1+y_1)+2(x_2+y_2)-(x_3+y_3)=0\ | \text{ zurück zur Menge} \\ \\
\Leftrightarrow\quad& (x_1+y_1,x_2+y_2,x_3+y_3)^T \in U \\ \\
\Leftrightarrow\quad& (x_1,x_2,x_3)^T+(y_1,y_2,y_3)^T\in U\\[2mm] \\
3)\quad& \text{Sei }(x_1,x_2,x_3)^T\in U,\ \lambda\in\mathbb{R}\ | \text{ dann gilt:} \\ \\
\Leftrightarrow\quad& 3x_1+2x_2-x_3=0\ \wedge\ \lambda\in\mathbb{R}\ | \cdot\lambda \\ \\
\Rightarrow\quad& \lambda\cdot(3x_1+2x_2-x_3)=\lambda\cdot 0\ | \text{ sortieren} \\ \\
\Leftrightarrow\quad& 3(\lambda\cdot x_1)+2(\lambda\cdot x_2)-(\lambda\cdot x_3)=0\ | \text{ zurück zur Menge} \\ \\
\Leftrightarrow\quad& (\lambda\cdot x_1,\lambda\cdot x_2,\lambda\cdot x_3)^T \in U \\ \\
\Leftrightarrow\quad& \lambda\cdot (x_1,x_2,x_3)^T \in U
\end{align*}

Weiteres Beispiel

Werden die Faktoren vor diesen Vektoren als variable Parameter aus $\mathbb{R}$ gesetzt, so ergibt sich daraus jede erdenkliche LK. Die Menge aller LKs bildet dann einen UVR. Im folgenden Beispiel einen UVR des $\mathbb{R}^3$, da die Vektoren aus dem $\mathbb{R}^3$ stammen:

\begin{align*}
& U:=\left\{\lambda_1\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+\lambda_2\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right) \ \Bigl|\Bigr.\ \lambda_1,\lambda_2\in\mathbb{R}\right\} \text{ ist UVR des }\mathbb{R}^3\text{, da:}
\end{align*}

\begin{align*}
1)\quad& 0\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+0\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)=\left(\begin{array}{c}{0}\\{0}\\{0}\end{array}\right)=\overrightarrow{0}\in U
\end{align*}

\begin{align*}
2)\quad \overrightarrow{x},\overrightarrow{y}\in U \quad&\overrightarrow{x}:=\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right)=\lambda_{1,x}\cdot\left(\begin{array}{c}{2}\\{-1}\\ \\{3}\end{array}\right)+\lambda_{2,x}\cdot\left(\begin{array}{c}{-2}{0}{-3}\end{array}\right)\text{ und}\\ \\
&\overrightarrow{y}:=\left(\begin{array}{c}{y_1}\\{y_2}\\{y_3}\end{array}\right)=\lambda_{1,y}\cdot\left(\begin{array}{c}{2}\\{-1}\\ \\{3}\end{array}\right)+\lambda_{2,y}\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)\\ \\
\stackrel{addieren}{\Rightarrow}&\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right)+\left(\begin{array}{c}{y_1}\\{y_2}\\ \\{y_3}\end{array}\right)=\Bigl(\underbrace{\lambda_{1,x}+\lambda_{1,y}}_{\in\,\mathbb{R}}\Bigr)\cdot\left(\begin{array}{c}{2}\\{-1}\\ \\{3}\end{array}\right)+\Bigl(\underbrace{\lambda_{2,x}+\lambda_{2,y}}_{\in\,\mathbb{R}}\Bigr)\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)\in U
\end{align*}

\begin{align*}
3)\quad \overrightarrow{x}\in U,\ \lambda\in\mathbb{R} \quad&\overrightarrow{x}:=\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right)=\lambda_1\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+\lambda_2\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)\text{ und }\lambda\in\mathbb{R}\\
\stackrel{multiplizieren}{\Rightarrow}&\lambda\cdot\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right)=\Bigl(\underbrace{\lambda\cdot\lambda_1}_{\in\,\mathbb{R}}\Bigr)\cdot\left(\begin{array}{c}{2}\\{-1}\\{3}\end{array}\right)+\Bigl(\underbrace{\lambda\cdot\lambda_2}_{\in\,\mathbb{R}}\Bigr)\cdot\left(\begin{array}{c}{-2}\\{0}\\{-3}\end{array}\right)\in U
\end{align*}

Beispiel mit Vektorraum der Polynome bis zum Grad $2$:

\begin{align*}
\quad 1)\quad& \overrightarrow{0}\in P_2(X)\quad 0\cdot x^2+0\cdot x+0=0\quad\text{korrekt (Nullpolynom enthalten)}\\[2mm]
2)\quad& \text{Sei }\overrightarrow{x}:=a_1x^2+b_1x+c_1\in P_2(X)\ \wedge\ \overrightarrow{y}:=a_2x^2+b_2x+c_2\in P_2(X)\\
\stackrel{addieren}{\Rightarrow}& \overrightarrow{x}+\overrightarrow{y}=a_1x^2+b_1x+c_1,a_2x^2+b_2x+c_2=\underbrace{(a_1+a_2)}_{\in\,\mathbb{R}}x^2+\underbrace{(b_1+b_2)}_{\in\,\mathbb{R}}x+\underbrace{(c_1+c_2)}_{\in\,\mathbb{R}}\in P_2(X)\\[2mm]
\quad 3)\quad& \text{Sei }\overrightarrow{x}:=ax^2+bx+c\in P_2(X),\ \lambda\in\mathbb{R}\\
\stackrel{multiplizieren}{\Rightarrow}& \lambda\cdot(ax^2+bx+c)=\underbrace{(\lambda a)}_{\in\,\mathbb{R}}x^2+\underbrace{(\lambda b)}_{\in\,\mathbb{R}}x+\underbrace{(\lambda c)}_{\in\,\mathbb{R}}\in P_2(X)
\end{align*}

Nullvektorraum

Der Nullvektorraum ist der Vektorraum, in dem nur der Nullvektor als Element enthalten ist.

• Der Nullvektorraum ist der kleinste Vektorraum, den es gibt (nur ein Element enthalten)
• Der Nullvektorraum ist ein UVR zu jedem anderen Vektorraum
• Demnach ist der Nullvektorraum auch der kleinste UVR zu jedem Vektorraum

Der Nullvektorraum hat als einziger Vektorraum die Dimension 0 und als einzig mögliche Basis den Nullvektor $\overrightarrow{0}$.

Aber Achtung! Der Nullvektor darf in keiner anderen Basis als in dieser vorkommen. Das ist lediglich ein Sonderfall!

Thema Vektorraum als Schaubild