Nullstellen numerisch bestimmen

Bei Funktionen, die analytisch nicht nach $x$ aufzulösen sind, z.B. $f(x)=\text{e}^x+x=0$, benötigen wir numerische Verfahren, um Näherungslösungen zu bestimmen.

Newton-Verfahren

Das Newton-Verfahren wird genutzt, um Nullstellen von Funktionen numerisch zu bestimmen/sich ihnen anzunähern. Das Verfahren läuft iterativ ab mit einem Startwert $x_0$. Mit Hilfe dieses Verfahrens lässt sich die Nullstelle extrem schnell approximieren. Allerdings kann es auch passieren, dass der Algorithmus nicht terminiert bei ungünstig gewähltem $x_0$.

Newtonverfahren – Vorgehen

• $f'(x)$ bestimmen ($x_0$ gegeben)
• \begin{align*}
  \text{1. Schritt: }x_1&=x_0-\frac{f(x_0)}{f'(x_0)}\notag\\
  \text{allg. n-ter Schritt: } x_n&=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}\quad(\ \ \overset{n \to \infty}{\longrightarrow}x \ \ )
  \end{align*}

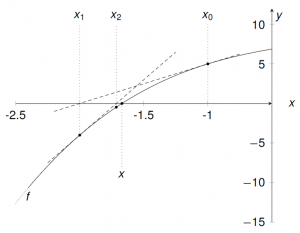
Grafisch: Bei $x_0$ starten; Tangente an den Graphen im Punkt $(x_0\,|\,f(x_0))$ zeichnen; Schnittpunkt mit der x-Achse ergibt $x_1$; usw…

Beispiele: Zwei Iterationsschritte

\begin{align*}
f(x)&=x^3+2x+8=0\\ \\
x_0&=-1\\ \\
f'(x)&=3x^2+2\\ \\
x_1&=-1-\frac{-1-2+8}{3+2}\\ \\
&=-1-\frac{5}{5}=-2\\ \\
x_2&=-2-\frac{-8-4+8}{12+2}\\ \\
&=-2-\frac{-4}{14}=-\frac{24}{14}\\ \\
&\approx -1{,}71
\end{align*}

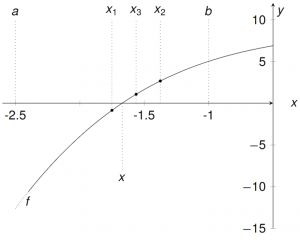
Bisektionsverfahren

Das Bisektionsverfahren wird ebenfalls genutzt, um Nullstellen von Funktionen numerisch zu bestimmen. Das Verfahren läuft iterativ ab mit einem Startintervall $[a,b]$ (bzw. $[a_0,b_0]$). Das Verfahren ist im Vergleich mit dem Newton-Verfahren relativ langsam, terminiert jedoch immer.

Bisektionsverfahren – Vorgehen

Voraussetzung: $f(a)<0<f(b)$, $f$ ist in $[a,b]$ stetig $\Rightarrow$ Nullstelle existiert durch den ZWS

• $x_n := \displaystyle{\frac{a_{n-1}+b_{n-1}}{2}}$ (Mittelwert des Intervalls)
• $f(x_n)=0 \Rightarrow x_n$ ist die gesuchte Nullstelle.
• $f(x_n)>0 \Rightarrow a_n:=a_{n-1}$ und $b_n:=x_n$
• $f(x_n)<0 \Rightarrow a_n:=x_n$ und $b_n:=b_{n-1}$

Beispiele: Drei Iterationsschritte

\begin{align*}
f(x)&=x^3+2x+8=0\\ \\
[a,b]&=[-2{,}5\, ,\, -1]\\ \\
f \text{ stetig}& \text{ und} \\ \\
f(-2{,}5)&<0<f(1) \text{ erfüllt.}\\ \\
\Rightarrow x_1 &= \frac{-2{,}5-1}{2}\\ \\
&=-1{,}75\\ \\
f(x_1)&\approx -0{,}86<0\\ a_1 &:=x_1\\ b_1 &:=b\\ \Rightarrow x_2 &= \frac{-1{,}75-1}{2}\\ &=-1{,}375\\ f(x_2)&\approx 2{,}65>0\\ \\
a_2 &:=a_1\\ \\
b_2 &:=x_2\\ \\
\Rightarrow x_3 &= \frac{-1{,}75-1{,}375}{2}\\ \\
&=-1{,}5625
\end{align*}