Reihen

Eine Reihe ist der Grenzwert der Partialsummen ($s_n$) einer Folge (hier $(a_k)_{k\in\mathbb{N}}$ ), sprich die Aufsummierung aller Folgenglieder von $a_k$:

\begin{align*}
\text{Erste Partialsumme}\quad s_1 &=\sum_{k=1}^{1}{a_k} = a_1\\
s_2 &=\sum_{k=1}^{2}{a_k} = a_1 + a_2\\
\vdots & \\
\text{n-te Partialsumme}\quad s_n &=\sum_{k=1}^{n}{a_k} = a_1 + a_2 + \ldots + a_n\\
\Rightarrow\quad\lim\limits_{n\to\infty}{s_n} &= \sum_{k=1}^{n}{a_k} = \sum_{k=1}^{\infty}{a_k}
\end{align*}

$ \sum_{k=1}^{\infty}{a_k} $ ist die (unendliche) Reihe!

Themen auf dieser Seite

• Grundlagen zu Reihen
• Bekannte Reihen
• Reihenwert berechnen
• Konvergenzkriterien
• Konvergenzverhalten zeigen
• Potenzreihen

Grundlagen zu Reihen

Im Allgemeinen geht es bei Reihen darum, Konvergenz oder Divergenz nachzuweisen. Bei speziellen Reihen lässt sich zudem ein Grenzwert berechnen. Es existiert dabei nicht die eine Lösung, Konvergenz oder Divergenz zu zeigen. Bei vielen Reihen funktioniert der Nachweis mit mehr als einem Kriterium. Die Auswahl eines Kriteriums, welches „funktioniert“, ist hier oft die große Hürde.

\begin{alignat*}{2}
&\sum_{k}^{\infty}{a_k} &&\quad \text{konvergiert }\rightarrow \text{ Konvergenz}\\ \\
&\sum_{k}^{\infty}{|{a_k}|} &&\quad \text{konvergiert }\rightarrow \text{ absolute Konvergenz}
\end{alignat*}

Damit gilt:
\begin{align}
&\sum_{k}^{\infty}{|{a_k}|} \text{ konvergent}\ \Rightarrow\ \sum_{k}^{\infty}{a_k} \text{ konvergent}\\ \\
&\sum_{k}^{\infty}{|{a_k}|}\geq|{\sum_{k}^{\infty}{a_k}|}\geq\sum_{k}^{\infty}{a_k}
\end{align}

Noch nicht verstanden? Dann schau dir dieses Erklärvideo an!

Rechenregeln

Aus einer Reihe dürfen konstante Faktoren (nicht vom derzeitigen Laufindex abhängig) herausgezogen werden, egal ob die Reihe konvergiert oder divergiert (eine konvergente Reihe bleibt konvergent; ein divergente Reihe wird auch durch das Herausziehen von konstanten Faktoren immer noch divergieren):
\begin{align}
&\sum_k^\infty{\lambda\cdot a_k}=\lambda\cdot\sum_k^\infty{a_k},\qquad \lambda\in\mathbb{R},\quad k\in\mathbb{Z}
\end{align}
Ähnlich wie bei Folgen gilt: Wenn zwei Reihen $\sum{a_k}$, $\sum{b_k}$ konvergent sind, so gilt
\begin{align}
&\left(\sum_k^\infty{a_k}\right)+\left(\sum_k^\infty{b_k}\right)=\sum_k^\infty{(a_k+b_k)}
\end{align}
Hier ist Vorsicht geboten! Wenn eine Summe $\sum_k^\infty{(a_k+b_k)}$ konvergiert, bedeutet das keineswegs, dass die einzelnen Reihen $\sum{a_k}$, $\sum{b_k}$ konvergent sind!

Falls zwei Reihen $\sum{a_k}$, $\sum{b_k}$ absolut konvergent sind, dann ist $\sum{c_k}$ mit
\begin{align}
&\sum_{k=0}^{\infty}{c_k}=\sum_{k=0}^{\infty}{\left(\sum_{n=0}^{k}{a_nb_{k-n}}\right)}=\left(\sum_{k=0}^{\infty}{a_k}\right)\cdot\left(\sum_{k=0}^{\infty}{b_k}\right)
\end{align}
ebenfalls absolut konvergent. Das Produkt wird Cauchy-Produkt dieser beiden Reihen genannt. Für eine Doppelreihe gilt allgemein:
\begin{align}
\begin{aligned}
\sum_{k=0}^{K}{\left(\sum_{n=0}^{N}{a_kb_n}\right)}&=(a_0b_0+a_0b_1+\ldots+a_0b_N)+(a_1b_0+a_1b_1+\ldots+a_1b_N)\\
&+\ldots+(a_Kb_0+a_Kb_1+\ldots+a_Kb_N)
\end{aligned}
\end{align}

Bekannte Reihen

Für die Grenzwertberechnung von speziellen Reihen müssen diese Reihen natürlich bekannt sein. Ebenfalls ist es wichtig (besonders für das Majoranten- und Minorantenkriterium) zu wissen, welche (Standard)Reihen konvergieren/divergiere.

Exponentialreihe:
\begin{align}
&\sum_{k=0}^{\infty}{\frac{x^k}{k!}} = \text{e}^x
\end{align}

Reihe des Logarithmus:
\begin{align}
&\sum_{k=0}^{\infty}{(-1)^{k}\frac{x^{k+1}}{k+1}} = \ln(x+1)\quad\text{ mit x > 1}
\end{align}

Reihendarstellungen der trigonometrischen Funktionen:
\begin{alignat}{2}
&\sum_{k=0}^{\infty}{(-1)^k\frac{x^{2k+1}}{(2k+1)!}} &&= \sin(x)\\ \\
&\sum_{k=0}^{\infty}{(-1)^k\frac{x^{2k}}{(2k)!}} &&= \cos(x)
\end{alignat}
Wichtig bei den oben genannten Reihen ist, dass der Laufindex bei 0 beginnt.

Teleskopreihe:

Dies ist keine explizite Reihe, sondern eher eine Eigenschaft, die diese besitzen. Bei Teleskopreihen lassen sich fast alle Summanden zu Null addieren. Daher stammt auch der Name, da sich die Reihe wie ein Teleskop „zusammenzieht“. Das gängigste Beispiel hierfür ist folgende Reihe:

\begin{alignat}{2}
&\sum_{k=1}^{\infty}{\left(\frac{1}{k(k+1)}\right)}&&\stackrel{\text{PBZ}}{=}\sum_{k=1}^{\infty}{\left(\frac{1}{k}-\frac{1}{k+1}\right)}=1,\quad\text{da}\label{teleskopreihe}\\ \\
&\sum_{k=1}^{n}{\left(\frac{1}{k}-\frac{1}{k+1}\right)}&&=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\ldots+\frac{1}{n}-\frac{1}{n+1}\notag\\ \\
& &&=1-\frac{1}{n+1}\overset{{n \to \infty}}{\longrightarrow}1-0=1\notag
\end{alignat}

Auch hier ist Vorsicht geboten! Untersuchen wir z.B. die Reihe $\sum_k^\infty{(-1)^k}$ und sagen, dass sich alle Summanden herauskürzen (da 1-1 immer 0 ist) und damit der Wert 0 ist, liegen wir falsch. Auf jeden Fall notwendig ist, dass die Folge in der Reihe eine Nullfolge ist.

Geometrische Reihe und deren Partialsumme:

\begin{align*}
\sum_{k=0}^{\infty}{q^k} \ &\overset{{|{q}|\text{<}1}}{=} \ \frac{1}{1-q}
\begin{cases}
|q|<1&\text{Reihe konvergiert}\\
|q|\geq 1&\text{Reihe divergiert}
\end{cases}\\
\sum_{k=0}^{n}{q^k}&=\frac{1-q^{n+1}}{1-q}
\end{align*}

Wenn lediglich Konvergenz oder Divergenz gezeigt werden muss, ist es egal, ab welcher Zahl der Laufindex k beginnt, wie z.B. bei der harmonischen Reihe.

(Allgemeine) Harmonische Reihe:

\begin{align}
&\sum_{k=1}^{\infty}{\frac{1}{k^a}}\; \begin{cases}a\leq 1&\text{Reihe divergiert}\\ a > 1&\text{Reihe konvergiert}\end{cases}\\ \\
&\sum_{k=1}^{\infty}{\frac{1}{k}} \quad \text{divergiert }(a=1)
\end{align}

Einige bekannte Grenzwerte:

Achtung: $k$ beginnt hier jeweils bei 1
\begin{alignat*}{3}
&\sum_{k=1}^{\infty}{\frac{1}{k^2}}=\frac{\pi^2}{6} \quad\qquad &&\sum_{k=1}^{\infty}{\frac{1}{k^4}}=\frac{\pi^4}{90} \quad\qquad &&\sum_{k=1}^{\infty}{\frac{1}{k^6}}=\frac{\pi^6}{945}\\ \\
&\sum_{k=1}^{\infty}{\frac{(-1)^{k+1}}{2k-1}}=\frac{\pi}{4}\quad\qquad &&\sum_{k=1}^{\infty}{\frac{(-1)^{k+1}}{k}}=\ln(2) \quad\qquad &&
\end{alignat*}

Summenformeln:

\begin{alignat}{2}
&\sum_{k=1}^{n}{k} &&= \frac{n(n+1)}{2}\quad (\text{Gauß’sche Summenformel})\\ \\
&\sum_{k=1}^{n}{k^2} &&= \frac{n(n+1)(2n+1)}{6}\\ \\
&\sum_{k=1}^{n}{k^3} &&= \left(\frac{n(n+1)}{2}\right)^2
\end{alignat}

Reihenwert berechnen

Um konkrete Werte einer Reihe berechnen zu können, muss diese in einer aus dem vorherigen Kapitel bekannter Darstellungsweise vorliegen. Eine Indexverschiebung wird benötigt, um Reihendarstellungen derart umschreiben zu können:

Arten der Indexverschiebung

1. Verschiebung durch Abändern des Laufindex innerhalb der Summe
2. Verschiebung durch Herausziehen/Hinzufügen von einzelnen Summanden

1. Art
\begin{align*}
\sum_{k=-1}^{\infty}\frac{2^{k+1}}{(k+1)!}=\sum_{k-1=-1}^{(k-1=)\infty}\frac{2^k}{(k-1+1)!}=\sum_{k=0}^{(k=)\infty+1}\frac{2^k}{k!}=\sum_{k=0}^{\infty}\frac{2^k}{k!}=\text{e}^2
\end{align*}

Falls bei einer solchen Indexverschiebung zu einem endlichen Wert aufsummiert wird, muss auch der Endwert entsprechend angepasst werden. Bei $\infty$ ist das natürlich nicht nötig.

2. Art
\begin{align*}
&\sum_{k=1}^{\infty}\frac{3^{k}}{k!}=\sum_{k=0}^{\infty}\frac{3^{k}}{k!}-\underbrace{\frac{3^0}{0!}}_{- 0. \text{Eintrag}}=\sum_{k=0}^{\infty}\frac{3^{k}}{k!}-1=\text{e}^3-1\\ \\
&\sum_{k=2}^{\infty}{\left(\frac{1}{3}\right)^k} = \sum_{k=0}^{\infty}{\left(\frac{1}{3}\right)^k} \underbrace{- 1}_{- 0. \text{Eintrag}}\underbrace{- \frac{1}{3}}_{- 1. \text{Eintrag}} = \frac{1}{1-\frac{1}{3}} – 1 – \frac{1}{3} = \frac{1}{6}
\end{align*}

Kombiniertes Beispiel
\begin{align*}
\sum_{n=0}^{\infty}\frac{4^{n}}{(n+2)!}&=\sum_{n-2=0}^{\infty}\frac{4^{n-2}}{(n+2-2)!}=\sum_{n=2}^{\infty}\frac{4^{-2}\cdot 4^n}{n!}\\ \\
&=4^{-2}\left(\sum_{n=0}^{\infty}\frac{4^n}{n!}-\frac{4^0}{0!}-\frac{4^1}{1!}\right)=4^{-2}\left(\text{e}^4-1-4\right)=\frac{1}{16}\cdot(\text{e}^4-5)
\end{align*}

Konvergenzkriterien

Es existieren eine handvoll Konvergenzkriterien, mit denen Reihen auf ihr Konvergenzverhalten untersucht werden können. Manche Kriterien eignen sich bei bestimmten Reihen besser als andere. Hier werden die Kriterien zunächst vorgestellt.

Nullfolgenkriterium

Mit dem Nullfolgenkriterium/Trivialkriterium/notwendigen Kriterium wird ausschließlich Divergenz nachgewiesen. Wenn wir bemerken, dass die Folge $a_k$ in der Reihe keine Nullfolge ist, ist sofort klar, dass die Reihe divergiert. Dann werden nämlich „im Unendlichen“ immer Werte addiert/subtrahiert, die sich nicht der Null nähern. Es ist somit unmöglich, dass die Reihe konvergieren kann.

Nullfolgenkriterium – Verfahren

• Nachweis: ausschließlich Divergenz (Die Umkehrung „Wenn es eine Nullfolge ist, konvergiert die Reihe“ gilt nicht!)
• Einsatz: Wenn $a_k$ keine Nullfolge ist

\begin{align}
\sum_{k=1}^{\infty}{a_k}\ , \quad \lim\limits_{k}{a_k} \neq 0 \Rightarrow \text{Die Reihe divergiert}
\end{align}

Schau dir zur Vertiefung das Erklärvideo zum Nullfolgekriterium an

Beispiele – Nullfolgenkriterium
\begin{align*}
&\sum_{k=1}^{\infty}{\frac{k}{2k+1}}\ , \quad \lim\limits_{k\to\infty}{a_k}=\lim\limits_{k\to\infty}{\frac{k}{2k+1}} = \frac{1}{2} \neq 0 \Rightarrow \text{Die Reihe divergiert}\\ \\
&\sum_{k=0}^{\infty}{\left(1+\frac{1}{k}\right)^k}\ , \quad \lim\limits_{k\to\infty}{a_k}=\lim\limits_{k\to\infty}{\left(1+\frac{1}{k}\right)^k} = \text{e} \neq 0 \Rightarrow \text{Die Reihe divergiert}\\ \\
&\sum_{k=1}^{\infty}{\sqrt[k]{\frac{1}{2k}}}\ , \quad \lim\limits_{k\to\infty}{a_k}=\lim\limits_{k\to\infty}{\sqrt[k]{\frac{1}{2k}}} = \lim\limits_{k\to\infty}{\frac{1}{\sqrt[k]{2}\sqrt[k]{k}}} = 1 \neq 0 \Rightarrow \text{Die Reihe divergiert}
\end{align*}

Beispiele – Umkehrung des Kriteriums gilt nicht
\begin{align*}
&\sum_{k=1}^{\infty}{\frac{1}{k^2}}\ , \quad \lim\limits_{k\to\infty}{a_k}=\lim\limits_{k\to\infty}{\frac{1}{k^2}} = 0 \quad \text{(Diese Reihe konvergiert)}\\ \\
&\sum_{k=1}^{\infty}{\frac{1}{k}}\ , \quad \lim\limits_{k\to\infty}{a_k}=\lim\limits_{k\to\infty}{\frac{1}{k}} = 0 \quad \text{(Aber diese Reihe divergiert)}
\end{align*}

Majorantenkriterium

Die Idee hierbei ist die Folge in der Reihe nach oben abzuschätzen, sodass eine bekannte Reihe herauskommt, die konvergiert.

Schau dir zur Einführung in das Majorantenkriterium dieses Erklärvideo an!

Majorantenkriterium – Verfahren

• Nachweis: ausschließlich (absolute) Konvergenz
• Einsatz: Wenn $a_k$ nur Polynome, Wurzeln, sin, cos enthält

\begin{align}
&\sum_{k=1}^{\infty}{a_k}\ ,\quad |{a_k}| \leq b_k \text{ mit } \sum_{k=1}^{\infty}{b_k}\\ \\
\text{Wenn für }&\sum{b_k} \text{ die Konvergenz bekannt ist, ist }\sum{b_k} \text{ Majorante für }\sum{a_k}\notag\\ \\
\Rightarrow &\sum_{k=1}^{\infty}{a_k}\text{ konvergiert.}\notag
\end{align}

Beispiel 1: Majorantenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{1}{2k(k+1)}}\ , \quad \text{da }|{\frac{1}{2k(k+1)}}|<\frac{1}{2k^2}<\frac{1}{k^2}\text{ gilt, ist }\sum_{k=1}^{\infty}{\frac{1}{k^2}}\text{ Majorante.}\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{1}{2k(k+1)}}\text{ konvergiert (absolut).}
\end{align*}

Beispiel 2: Majorantenkriterium
\begin{align*}
\sum_{k=0}^{\infty}&{\frac{k\sqrt{2^k}}{(k+1)2^k}}\ , \quad \text{da }|{\frac{k\sqrt{2^k}}{(k+1)2^k}}|<\frac{k\sqrt{2^k}}{k2^k}=\left(\frac{\sqrt{2}}{2}\right)^k=\left(\frac{1}{\sqrt{2}}\right)^k\text{ gilt,}\\ \\
&\text{ist }\sum_{k=1}^{\infty}{\left(\frac{1}{\sqrt{2}}\right)^k}\text{ Majorante (geometrische Reihe mit \frac{1}{\sqrt{2}}=q).}\\ \\
&\Rightarrow \sum_{k=0}^{\infty}{\frac{k\sqrt{2^k}}{(k+1)2^k}}\text{ konvergiert (absolut).}
\end{align*}

Beispiel 3: Majorantenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{\sqrt{k^2+1}-\sqrt{k^2-1}}{k}}\ , \quad \text{mit „1“ erweitert ergibt (3. bin. Formel nutzen): }\\ \\
&\text{da }|{\frac{\sqrt{k^2+1}-\sqrt{k^2-1}}{k}\cdot \frac{\sqrt{k^2+1}+\sqrt{k^2-1}}{\sqrt{k^2+1}+\sqrt{k^2-1}}}|=|{\frac{(k^2+1)-(k^2-1)}{k(\sqrt{k^2+1}+\sqrt{k^2-1})}}|\\ \\
&=|{\frac{2}{k(\sqrt{k^2+1}+\sqrt{k^2-1})}}\stackrel{\ast^1}|{<}\frac{2}{k(\sqrt{k^2+1})}<\frac{2}{k\sqrt{k^2}}=\frac{2}{k^2}\text{ gilt,}\\ \\[2mm]
&\text{ist }\sum_{k=1}^{\infty}{\frac{2}{k^2}}=2\sum_{k=1}^{\infty}{\frac{1}{k^2}}\text{ Majorante.}\\[2mm] &\Rightarrow \sum_{k=1}^{\infty}{\frac{\sqrt{k^2+1}-\sqrt{k^2-1}}{k}}\text{ konvergiert (absolut).} \end{align*}

Minorantenkriterium

Die Idee ist ähnlich dem Majorantenkriterium, jedoch genau umgekehrt: Die Folge in der Reihe nach unten abzuschätzen, sodass eine bekannte Reihe herauskommt, die divergiert.

In diesem Video erklärt Daniel das Minorantenkriterium

Minorantenkriterium – Verfahren

• Nachweis: ausschließlich Divergenz
• Einsatz: Wenn $a_k$ nur Polynome, Wurzeln, sin, cos enthält

\begin{align}
&\sum_{k=1}^{\infty}{a_k}\ ,\quad a_k \geq b_k \text{ mit } \sum_{k=1}^{\infty}{b_k}\\ \\
\text{Wenn für }&\sum{b_k} \text{ die Divergenz bekannt ist, ist }\sum{b_k} \text{ Minorante für }\sum{a_k}\notag\\ \\
\Rightarrow &\sum_{k=1}^{\infty}{a_k}\text{ divergiert.}\notag
\end{align}

Beispiel 1: Minorantenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{1}{\sqrt[3]{k}}}\ , \quad \text{da }\frac{1}{\sqrt[3]{k}}>\frac{1}{\sqrt[3]{k^3}}=\frac{1}{k}\text{ gilt, ist }\sum_{k=1}^{\infty}{\frac{1}{k}}\text{ Minorante.}\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{1}{\sqrt[3]{k}}}\text{ divergiert.}
\end{align*}

Beispiel 2: Minorantenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{1}{2k-1}}\ , \quad \text{da }\frac{1}{2k-1}>\frac{1}{2k}\text{ gilt, ist }\sum_{k=1}^{\infty}{\frac{1}{2k}}\text{ Minorante.}\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{1}{2k-1}}\text{ divergiert.}
\end{align*}

Hier eine Visualisierung der Vorgehensweise beim Majo- und Minorantenkriterium. Das ist rein mathematisch nicht wirklich präzise, aber es sollte dir helfen, die Verfahren besser zu verstehen.

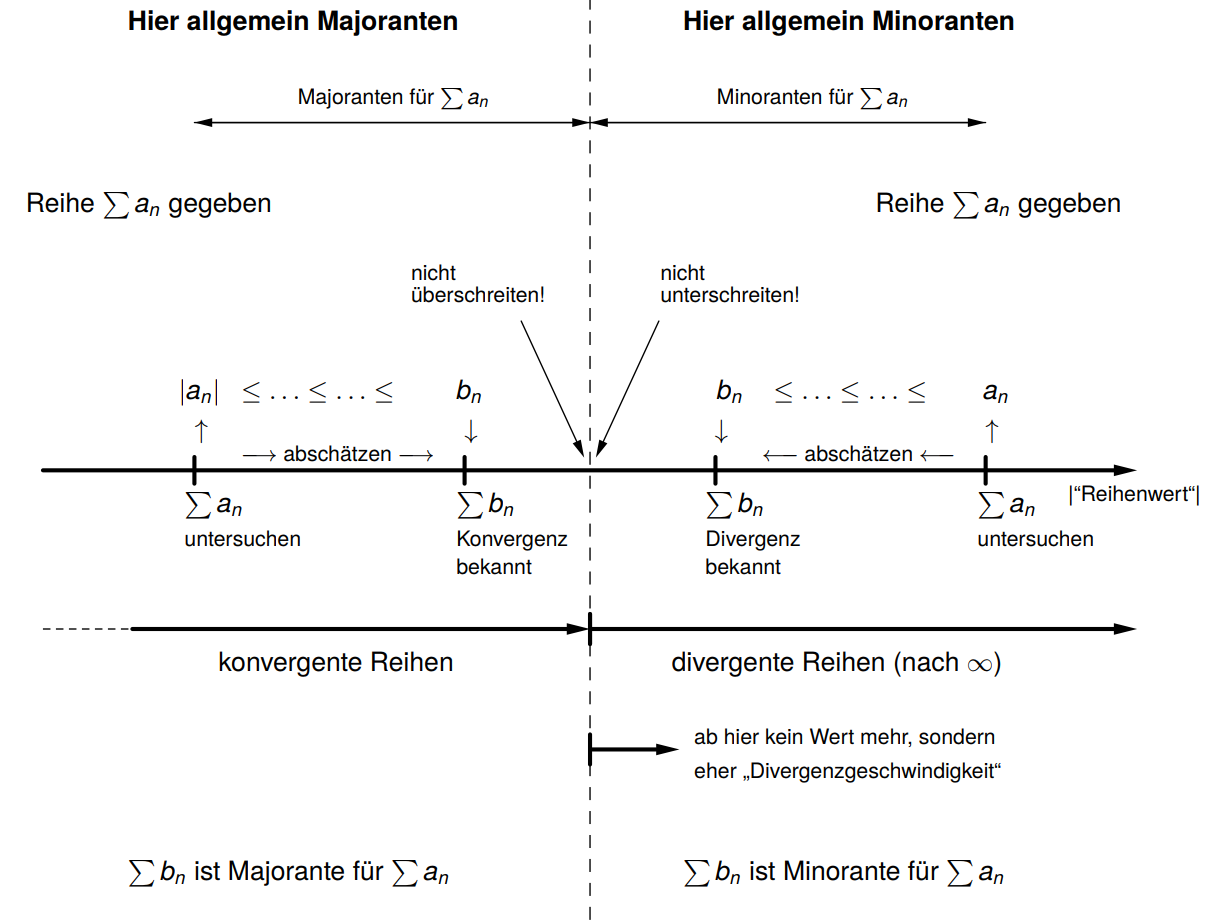
Quotientenkriterium

Mit dem Wurzelkriterium das umfassendste (und für dich wahrscheinlich wichtigste) Kriterium zum Nachweis von Konvergenz/Divergenz.
Quotientenkriterium – Verfahren

• Nachweis: absolute Konvergenz und Divergenz
• Einsatz: Quasi alles, außer wenn $a_k$ nur Polynome, Wurzeln, sin, cos enthält

\begin{align}
\text{Reihe }&\sum_{k=1}^{\infty}{a_k}\ ,\quad \left|\frac{a_{k+1}}{a_k}\right| \overset{{k \to \infty}}{\longrightarrow} q \begin{cases}q<1&\text{absolute Konvergenz}\\q>1&\text{Divergenz}\\q=1&\text{keine Aussage möglich}\end{cases}
\end{align}

Beispiel von Daniel zum Quotientenkriterium

Beispiel 1: Quotientenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{3^{2k}}{k!}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{3^{2(k+1)}}{(k+1)!}}{\frac{3^{2k}}{k!}}\right|=\frac{3^{2k+2}}{k!(k+1)}\cdot \frac{k!}{3^{2k}}=\frac{3^2}{k+1}\overset{{k \to \infty}}{\longrightarrow} 0\stackrel{\ast^1}{<}1\\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{3^{2k}}{k!}}\text{ konvergiert (absolut) nach dem Quotientenkriterium.}
\end{align*}

$*^1:$ Das < 1 muss hier auf jeden Fall notiert werden!

Beispiel 2: Quotientenkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{1}{k^k}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{1}{(k+1)^{k+1}}}{\frac{1}{k^k}}\right|=\frac{k^k}{(k+1)^{k+1}}=\frac{k^k}{(k+1)(k+1)^k}\\ \\
&=\frac{1}{k+1}\cdot \underbrace{\left(\frac{k}{k+1}\right)^k}_{< 1\text{ für alle } k\in\mathbb{N}}\overset{{k \to \infty}}{\longrightarrow} 0<1\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{1}{k^k}}\text{ konvergiert (absolut) nach dem Quotientenkriterium.}
\end{align*}

Beispiel 3: Quotientenkriterium
\begin{align*}
\sum_{k=0}^{\infty}&{\frac{k^k}{(2k)!}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{(k+1)^{k+1}}{(2(k+1))!}}{\frac{k^k}{(2k)!}}\right|\stackrel{\ast^1}{=}\frac{(k+1)(k+1)^k}{(2k)!(2k+1)(2k+2)}\cdot \frac{(2k)!}{k^k}\\ \\
&=\frac{(k+1)^k}{2(2k+1)k^k}=\frac{1}{4k+2}\cdot \left(\frac{k+1}{k}\right)^k=\frac{1}{4k+2}\cdot \underbrace{\left(1+\frac{1}{k}\right)^k}_{\rightarrow\ \text{e}}\overset{{k \to \infty}}{\longrightarrow}0<1\\ \\
&\Rightarrow \sum_{k=0}^{\infty}{\frac{k^k}{(2k)!}}\text{ konvergiert (absolut) nach dem Quotientenkriterium.}
\end{align*}

$*^1:$ Hier muss darauf geachtet werden, dass die Fakultät richtig umgeschrieben und anschließend richtig gekürzt wird. Erfahrungsgemäß passieren hierbei häufig Fehler!

Beispiel 4: Quotientenkriterium
\begin{align*}
\sum_{k=0}^{\infty}&{\frac{k^k}{k!}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{(k+1)^{k+1}}{(k+1)!}}{\frac{k^k}{k!}}\right|=\frac{(k+1)(k+1)^k}{k!(k+1)}\cdot \frac{k!}{k^k}\\ \\
&=\frac{(k+1)^k}{k^k}=\left(1+\frac{1}{k}\right)^k \overset{{k \to \infty}}{\longrightarrow} \text{e}>1\\ \\
&\Rightarrow \sum_{k=0}^{\infty}{\frac{k^k}{k!}}\text{ divergiert nach dem Quotientenkriterium.}
\end{align*}

Beispiel 5: Quotientenkriterium
\begin{align*}
\sum_{k=0}^{\infty}&{\frac{1}{2k-1}}\ , \quad \left|\frac{a_{k+1}}{a_k}\right|=\left|\frac{\frac{1}{2(k+1)-1}}{\frac{1}{2k-1}}\right|=\frac{2k-1}{2k+1}\overset{{k \to \infty}}{\longrightarrow} 1=1\\
&\Rightarrow \text{Keine Aussage über das Konvergenzverhalten möglich.}
\end{align*}

Bei dieser Reihe muss also ein anderes Kriterium verwendet werden als das Quotientenkriterium, um etwas über das Konvergenzverhalten sagen zu können.

Wurzelkriterium

Mit dem Quotientenkriterium das umfassendste (und für dich wahrscheinlich wichtigste) Kriterium zum Nachweis von Konvergenz/Divergenz.

Verfahren

• Nachweis: absolute Konvergenz und Divergenz
• Einsatz: Quasi alles, außer wenn $a_k$ nur Polynome, Wurzeln, sin, cos enthält

\begin{align}
\text{Reihe }&\sum_{k=1}^{\infty}{a_k}\ ,\quad \sqrt[k]{|{a_k}|} \overset{k \to \infty}\rightarrow q \begin{cases}q<1&\text{absolute Konvergenz}\\q>1&\text{Divergenz}\\q=1&\text{keine Aussage möglich}\end{cases}
\end{align}

Beispiel 1
\begin{align*}
\sum_{k=1}^{\infty}&{\left(\frac{k+7}{2k+1}\right)^k}\ , \quad \sqrt[k]{|{a_k}|}=\sqrt[k]{\left|\left(\frac{k+7}{2k+1}\right)^k\right|}= \frac{k+7}{2k+1} \overset{k\to\infty}\longrightarrow {\frac{1}{2}} \text{<} 1
\\&\Rightarrow \sum_{k=1}^{\infty}{\left(\frac{k+7}{2k+1}\right)^k}\text{ konvergiert (absolut) nach dem Wurzelkriterium.}
\end{align*}

Beispiel 2
\begin{align*}
\sum_{k=1}^{\infty}&{\frac{2^{k^2+1}}{3^{3k}}}\ , \quad \sqrt[k]{|{a_k}|}=\sqrt[k]{\left|\frac{2^{k^2+1}}{3^{3k}}\right|}=\sqrt[k]{\frac{2^{k^2}\cdot 2^1}{(3^3)^k}}=\frac{2^k\cdot\sqrt[k]{2}}{27}\overset{k \to \infty}\longrightarrow \infty>1\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{2^{k^2+1}}{3^{3k}}}\text{ divergiert nach dem Wurzelkriterium.}
\end{align*}

\begin{align*}
\sum_{k=1}^{\infty}&{\frac{\left(1+(-1)^k\right)^{2k}}{5k+k^5+5^k}}\ , \quad \sqrt[k]{|{a_k}|}=\sqrt[k]{\left|\frac{\left(1+(-1)^k\right)^{2k}}{5k+k^5+5^k}\right|}=\frac{\left(1+(-1)^k\right)^{2}}{\sqrt[k]{5k+k^5+5^k}}\\ \\
&\stackrel{\ast^1}{<}\frac{\left(1+1\right)^{2}}{\sqrt[k]{5k+k^5+5^k}}=\frac{4}{\sqrt[k]{5k+k^5+5^k}}\ \ast^2\overset{k \to \infty}\longrightarrow {\frac{4}{5}}<1\\ \\
&\Rightarrow \sum_{k=1}^{\infty}{\frac{\left(1+(-1)^k\right)^{2k}}{5k+k^5+5^k}}\text{ konvergiert (absolut) nach dem Wurzelkriterium.}
\end{align*}

$*^1$ Den Term $(-1)^k$ oben abzuschätzen war erlaubt, da der Grenzwert von $\sqrt[k]{|{a_k}|}$ < 1 bleibt. Daher ist die Schlussfolgerung der absoluten Konvergenz korrekt

$*^2$ Grenzwert von $\sqrt[k]{5k+k^5+5^k}$ ist 5, zeigen z.B. durch Vergleichskriterium.

Leibnizkriterium

Mit dem Leibnizkriterium kann nur Konvergenz einer alternierenden Reihe nachgewiesen werden. Ausschlaggebend für die Verwendung des Leibnizkriteriums ist, dass die Folge $a_k$ mit jedem nächstgrößeren k das Vorzeichen wechselt (sie alterniert):

Leibnizkriterium – Verfahren

• Nachweis: ausschließlich Konvergenz
• Einsatz: Für alternierende Reihen

\begin{align}
&\text{Alternierende Reihe }\sum_{k=1}^{\infty}{a_k}\quad\text{mit}\quad a_k=(-1)^k\cdot(\ldots)\\ \\
&\quad\text{1.} \overset{k\to \infty}{\longrightarrow}{|{a_k}|} = 0 \quad \text{und} \quad \text{2.} \ |{a_k}|\text{ monoton}\ \Rightarrow\ \text{Konvergenz}
\end{align}

Beispiel: Leibnizkriterium
\begin{align*}
\sum_{k=1}^{\infty}&{(-1)^k\frac{k+1}{2k^2}}\ ,\quad \text{alternierende Reihe:}\quad \text{1.}\ \ |{(-1)^k\frac{k+1}{2k^2}}| \ \ 0 \ \ \text{für} \ \ k \ \ \rightarrow \infty \\ \\
&\hspace{1cm}\begin{array}{rrcl}
\text{2.} &|{a_{k+1}}|&<&|{a_k}|\\ \\
\Leftrightarrow& \frac{k+2}{2(k+1)^2}&<&\frac{k+1}{2k^2}\\ \\
\Leftrightarrow& 2k^2(k+2)&<&2(k+1)^3\\ \\
\Leftrightarrow& k^3+2k^2&<&k^3+3k^2+3k+1\\ \\
\Leftrightarrow& 0&<&k^2+3k+1\\ \\
\end{array}\\[3mm]
\Rightarrow& \sum_{k=1}^{\infty}{(-1)^k\frac{k+1}{2k^2}} \ \ \text{ konvergiert.}
\end{align*}

Konvergenzverhalten

Im vorherigen Kapitel sind die verschiedenen Konvergenzkriterien beschrieben worden. Jedoch fehlt bei vielen Studierenden in irgendeiner Art und Weise der Blick dafür, bei gegebener Reihe ein funktionierendes Kriterium (vlt. sogar das am schnellsten funktionierende) auszuwählen. Es folgen zwei Unterkapitel, die dir den Weg dahin leichter machen sollen. Um das alles jedoch zu verinnerlichen, hilft es nur, sehr viele Reihen selbstständig zu untersuchen, und so die beschriebenen Schritte nachzuvollziehen und zu verinnerlichen.

Nachweis mit System
Ein 100%ig funktionierendes Kochrezept hierfür gibt es nicht, empfehlenswert ist für eine gegebene Reihe $\sum_{k}^{\infty}{a_k}$ die folgenden Punkte abzugehen:

Systematisches Vorgehen zum Konvergenz-/Divergenznachweis von Reihen

1. Kann ein Wert ausgerechnet werden?$ \quad \text{ja} \rightarrow \text{Konvergenz}\\ \text{nein} \rightarrow \text{weiter mit 2.}$

1. $a_k$ Nullfolge?$ \quad \text{ja} \rightarrow \text{weiter mit 3.} \\ \text{nein} \rightarrow \text{Nullfolgenkrit.} \rightarrow \text{Divergenz} $

1. $a_k$ alternierend?$ \quad \text{ja} \rightarrow \text{Leibnizkrit. versuchen}\\ \text{nein} \rightarrow \text{weiter mit 4.} $

1. Sind Fakultäten in $a_k$?$ \quad \text{ja} \rightarrow \text{Quotientenkrit. versuchen}\\ \text{nein} \rightarrow \text{weiter mit 5.} $

1. Sind Faktoren mit k im Exponenten in $a_k$?$ \quad\text{ja} \rightarrow \text{Wurzelkrit. versuchen}\\ \text{nein} \rightarrow \text{weiter mit 6.} $

1. Enthält $a_k$ nur Polynome, Wurzeln, sin, cos Terme?$\quad\cdots$ $ \text{ja} \rightarrow \text{Mino-/Majorantenkrit. versuchen}\\ \text{nein} \rightarrow \text{weiter mit 7.} $

1. Bel. Kriterium versuchen $\ldots$ evtl. Annahmen + Widerspruchsbeweis

Konvergenz abschätzen

Es ist möglich, das Konvergenzverhalten von vielen Reihen — ohne jegliche Rechnung — im Vorfeld abzuschätzen. Wir empfehlen dir an dieser Stelle erst weiter zu lesen, wenn du schon ein paar Übungsaufgaben zum Bestimmen von Konvergenzverhalten bearbeitet hast. Ansonsten könnte dich dieses Kapitel mehr verwirren als dir nützen.

Wie du bereits wissen solltest, kann eine Reihe nur dann konvergieren, wenn die zugehörige Folge eine Nullfolge ist. Doch wann konvergiert sie dann auch tatsächlich?

Folgendes Schema kann als erste Anlaufstelle betrachtet werden, das Konvergenzverhalten abzuschätzen (mit n als Laufvariable – also $\sum_{n=\ldots}^\infty{\ldots}$):

\begin{array}
Fkt.-Typ & Konstanten & Polynome/Potenzfkt. & Exponentialfkt. & Fakultäten \\
& a & n^a & a^n & n!
\end{array}

Faustregel: Die weiter rechts stehenden Tabellenspalten „dominieren“ die weiter links stehenden. Damit ist gemeint: Wenn die Folge in der Reihe ein Bruch mit Ausdrücken aus der oben stehenden Tabelle ist (was aller meistens der Fall ist!), konvergiert/divergiert die Reihe (höchstwahrscheinlich), je nachdem welcher Fkt.-Typ im Zähler und Nenner steht.

Konstante Faktoren spielen überhaupt keine Rolle, da sie immer aus der Reihe herausgezogen werden können.

sin(…)- und cos(…)-Terme als Summanden werden, egal was als „…“ steht, wie Konstanten behandelt, da sie das Intervall [-1,1] nie verlassen (sie sind beschränkt).

Achtung: Es gibt Ausnahmen (z. B. Spalte Polynome/Potenzfkt. dominiert erst ab „höchster Exponent“ > 1 die Konstanten

\begin{array}
\\
\textbf{Fkt.-Typ} & \textbf{Konstanten} & \textbf{Polynome/Potenzfkt.} & \textbf{Exponentialfkt.}\ & \textbf{Fakultäten} \\
\#1 & 2 & n^2+1 & 3^n & n! \\
\#2 & 3 & \sqrt{n} & 2\cdot 4^n & 3n! \\
\#3 & 13 & 6n^5-2n^2+n & 2^{n+1} & (2n)!
\end{array}

Beispiele von Kombinationen aus #1
\begin{align*}
\text{a}_1) \ \sum_{n=1}^\infty{\frac{2}{3^n}},\quad \text{b}_1)\ \sum_{n=1}^\infty{\frac{n!}{n^2+1}},\quad \text{c}_1)\ \sum_{n=1}^\infty{\frac{3^n}{n^2+1}}, \quad \text{d}_1)\ \sum_{n=1}^\infty{\frac{2}{n^2+1}}
\end{align*}

$a_1)$ wird konvergieren ($3^n$ im Nenner dominiert die Konstante)
$b_1)$ wird divergieren ($n!$ im Zähler dominiert das Polynom)
$c_1)$ wird divergieren ($3^n$ im Zähler dominiert das Polynom)
$d_1)$ wird konvergieren ($n^2+1$ im Nenner dominiert die Konstante, da höchster Exponent =2>1)

Beispiele von Kombinationen aus #2
\begin{align*}
\text{a}_2) \ \sum_{n=1}^\infty{\frac{\sqrt{n}}{2\cdot 4^n}},\quad \text{b}_2)\ \sum_{n=1}^\infty{\frac{3}{\sqrt{n}}},\quad \text{c}_2)\ \sum_{n=1}^\infty{\frac{3n!}{2\cdot 4^n}}, \quad \text{d}_2)\ \sum_{n=1}^\infty{\frac{\sqrt{n}}{3n!}}
\end{align*}

$a_2)$ wird konvergieren ($4^n$ im Nenner dominiert die Potenzfunktion $\sqrt{n}$)
$b_2)$ wird divergieren ($\sqrt{n}$ im Nenner dominiert nicht die Konstante 3, da höchster Exponent $=\frac{1}{2}\leq 1$)
$c_2)$ wird divergieren ($n!$ im Zähler dominiert die Exp.fkt. $4^n$)
$d_2)$ wird konvergieren ($n!$ im Nenner dominiert Potenzfunktion $\sqrt{n}$)

Beispiele von Kombinationen aus #3
\begin{align*}
\text{a}_3)\ \sum_{n=1}^\infty{\frac{6n^5-2n^2+n}{(2n)!}},\ \text{b}_3)\ \sum_{n=1}^\infty{\frac{13}{6n^5-2n^2+n}},\ \text{c}_3)\ \sum_{n=1}^\infty{\frac{13}{2^{n+1}}},\ \text{d}_3)\ \sum_{n=1}^\infty{\frac{(2n)!}{2^{n+1}}}
\end{align*}

$a_3)$ wird konvergieren ($(2n)!$ im Nenner dominiert das Polynom $6n^5-2n^2+n$)
$b_3)$ wird konvergieren ($6n^5-2n^2+n$ im Nenner dominiert die Konstante 13, da höchster Exponent $=5 > 1$)
$c_3)$ wird konvergieren ($2^n$ im Nenner dominiert die Konstante 13; beachte $2^{n+1}=2\cdot 2^n$)
$d_3)$ wird divergieren ($(2n)!$ im Zähler dominiert die Exp.fkt $2^n$)

Was müssen wir aber nun zur Vorüberlegung beachten, wenn mehrere Funktionstypen (gemischt) auftauchen?

Konstanten: Sind im Allgemeinen recht unwichtig, zumal sie eigentlich Polynome mit Grad 0 sind.

Polynome/Potenzfkt.: Tauchen ausschließlich Polynome/Potenzfkt. in der Reihe auf, kommt es auf den Unterschied der höchsten Exponenten im Zähler und Nenner an! Dies ist wichtig zum korrekten Anwenden von Majo- und Minorantenkriterium, da die anderen Kriterien bei dieser Art Reihe versagen! Also:
\begin{align}
\text{„höchst. Exp. Nenner“ }-\text{„höchst. Exp. Zähler“}
\begin{cases} \leq 1 & \text{Reihe div.} \\ > 1 & \text{Reihe konv.} \end{cases}
\end{align}

Exponentialfunktionen: Kommen Exponentialfunktionen im Zähler und Nenner (auch gemischt mit Polynomen/Potenzfkt.) vor, kommt es auf die größere Basis an (z. B. $3^n$ dominiert $2^n$).

Fakultäten: Kommen Fakultäten im Zähler und Nenner (auch gemischt mit Exponentialfkt. und Polynomen/Potenzfkt.) vor, kommt es auf den größeren Vorfaktor in der Fakultät an (z. B. (4n)! dominiert (3n)!)

Dabei spielt es keine Rolle, ob die jeweiligen Terme im Zähler und im Nenner addiert oder multipliziert werden.

Beispiele zur Vorüberlegung zum Konvergenzverhalten
\begin{align*}
\begin{array}{*4{>{\displaystyle}l}}
a)\ \sum_{n=1}^\infty{\frac{5n-1}{n^2+n+1}} & b)\ \sum_{n=1}^\infty{\frac{3^n+n^2}{1+2^n}} & c)\ \sum_{n=1}^\infty{\frac{3^{n+1}+1}{2^{2n}}} & d)\ \sum_{n=1}^\infty{\frac{4^n\cdot n!}{(2n)!}} \\[6mm]
e)\ \sum_{n=1}^\infty{\frac{n^6\cdot 2^n}{2+n!}} & f)\ \sum_{n=1}^\infty{\frac{\sqrt{n^3}+n}{n^3+n^2+1}} & g)\ \sum_{n=1}^\infty{\frac{3^{n^2}}{6^n+n}} & h)\ \sum_{n=1}^\infty{\frac{(n!)^2}{(2n)!}}
\end{array}
\end{align*}

a) Nur Polynome im Zähler und Nenner! Aus Gl. (\ref{eq:faustformelmajorantenminorantenkriterium}): „`Höchst. Exp. Nenner“‚ – „`höchst. Exp. Zähler“‚ $=2-1=1\leq 1$. Also wird die Reihe divergieren.

b) Exponentialfkt. dominieren! Da $3^n$ im Zähler und $3>2$, wird die Reihe divergieren.

c) Exponentialfkt. dominieren! Achtung: $2^{2n}=(2^2)^n=4^n$ (und $3^{n+1}=3\cdot 3^n[latex]). Da [latex]4^n$ im Nenner und $4>3$, wird die Reihe konvergieren.

d) Fakultäten dominieren! Da $(2n)!$ im Nenner und Vorfaktor in der Fakultät $2>1$, wird die Reihe konvergieren.

e) Fakultät dominiert. Da $n!$ im Nenner, wird die Reihe konvergieren.

f) Nur Polynome und Potenzfkt. im Zähler und Nenner! Achtung: $\sqrt{n^3}=n^{\frac{3}{2}}$. „Höchst. Exp. Nenner“‚ – „höchst. Exp. Zähler“ $=3-\frac{3}{2}=\frac{3}{2}>1$. Also wird die Reihe konvergieren.

g) Ohne weiteres mit den beschriebenen Vorüberlegungen keine Aussage treffbar, da nicht abschätzbar, wie sich $3^{n^2}$ verhalten wird (Beachte: $3^{n^2}=3^{(n^2)}\neq (3^n)^2=3^{2n}$).

h) Ohne weiteres mit den beschriebenen Vorüberlegungen keine Aussage treffbar, da nicht abschätzbar, wie sich $(n!)^2$ verhalten wird.

Für die Interessierten: Warum funktioniert das Ganze?

Diese inoffiziellen „Regeln“ zur Vorüberlegung zum Konvergenzverhalten von Reihen basieren auf der allgemeinen Anwendung des Quotientenkriteriums (alle Regeln mit Exponentialfunktion- und Fakultätanteilen) und der allgemeinen harmonischen Reihe zum korrekten Abschätzen. Was mit den Termen beim Quotientenkriterium passiert und warum sich daraus die „Regeln“ ableiten, soll hier kurz gezeigt werden:

Zur späteren Begriffsstütze: Mit

\begin{align*}
\quad \sum_{n=1}^\infty{c_n}, \quad |{\frac{c_{n+1}}{c_n}}|=\dots=\widetilde{c_n}\overset{n\to\infty}{\longrightarrow} \ \underbrace{\tilde{c}}_{\textrm{GW des Quot.krit.}}
\end{align*}

Was passiert mit Polynomen/Potenzfkt. bei Anwendung des Quotientenkriteriums? Mit $a,b\in\mathbb{R}$:

\begin{align*}
\sum_{n=1}^\infty{\frac{n^a}{n^b}},\quad|{\frac{\frac{(n+1)^a}{(n+1)^b}}{\frac{n^a}{n^b}}}|=\frac{(n+1)^a\cdot n^b}{(n+1)^b\cdot n^a}=\frac{n^an^b+\ldots}{n^bn^a+\ldots}=\frac{n^{a+b}+\ldots}{n^{a+b}}\overset{n\to\infty}{\longrightarrow}1
\end{align*}

Völlig egal, wie viele Summanden die Polynome/Potenzfkt. in $c_n$ haben, beim Quotientenkriterium ist der höchste Exponent (und der zugehörige Vorfaktor) im Zähler und Nenner von $\widetilde{c_n}$ derselbe. Nach bekannter Folge ist der Grenzwert also immer 1 und es lässt sich so keine Aussage treffen. Also muss hier auf das Abschätzen zurückgegriffen werden.

Was passiert mit Exponentialfkt. bei Anwendung des Quotientenkriteriums? Mit $a,b\in\mathbb{R}[\latex]:
\begin{align*}
\sum_{n=1}^\infty{\frac{a^n}{b^n}},\quad|{\frac{\frac{a^{n+1}}{b^{n+1}}}{\frac{a^n}{b^n}}}|=\frac{a^{n+1}\cdot b^n}{b^{n+1}\cdot a^n}=\frac{a}{b}\overset{n\to\infty}{\longrightarrow}\frac{a}{b}
\end{align*}

Aus Exponentialfkt. wird am Ende also ein Faktor (hier [latex]\frac{a}{b}$). Bedeutet, bei $a<b$ konvergiert und bei $a>b$ divergiert die Reihe. Kommen Exponentialfkt. mit Polynomen gleichzeitig in der Reihe vor, haben die Polynome also keinen Einfluss auf den „`Grenzwert des Quotientenkriteriums“ ($\tilde{c}$).

Was passiert mit Fakultäten bei Anwendung des Quotientenkriteriums?
\begin{align*}
\sum_{n=1}^\infty{\frac{(an)!}{(bn)!}},&\quad|{\frac{\frac{(a(n+1))!}{(b(n+1))!}}{\frac{(an)!}{(bn)!}}}|=\frac{(an+a)!\cdot (bn)!}{(bn+b)!\cdot (an)!}\\ \\
=\ &\frac{{(an)!}(an+1)(an+2)\cdots(an+(a-2))(an+(a-1))(an+a)\cdot {(bn)!}}{{gray}{(bn)!}(bn+1)(bn+2)\cdots(bn+(b-2))(bn+(b-1))(bn+b)\cdot {(an)!}}\\ \\
=\ &\frac{\overbrace{(an+1)(an+2)\cdots(an+(a-2))(an+(a-1))(an+a)}^{a~\text{Linearfaktoren bzw. Polynom von Grad $a$}}}{\underbrace{(bn+1)(bn+2)\cdots(bn+(b-2))(bn+(b-1))(bn+b)}_{b~\text{Linearfaktoren bzw. Polynom von Grad $b$}}}=\frac{a^a\cdot n^a+\ldots}{b^b\cdot n^b+\ldots}
\end{align*}

Aus Fakultäten wird am Ende ($\widetilde{c_n}$) also jew. ein Polynom vom Grad des Vorfaktors in der Fakultät. Das ist der Grund, warum Fakultäten die Exponentialfkt. und Polynome/Potenzfkt. dominieren, denn als Folge (im Term $\widetilde{c_n}$) dominiert das Polynom (von mindestens Grad 1) alle konstanten Faktoren im Grenzwert.

Beispiel – Komplett alle Gedankengänge mit Rechnungen:
\begin{align*}
\text{Reihe }\sum_{n=2}^\infty{\frac{6n\cdot 3^n}{2^n\cdot n!}}\text{ gegeben.}
\end{align*}

Vorüberlegung: Fakultät dominiert! Da $n!$ im Nenner, wird diese Reihe konvergieren.

Auswahl des Kriteriums: Quotientenkriterium, da eine Fakultät auftritt.
\begin{align*}
|{\frac{\frac{6(n+1)\cdot 3^{n+1}}{2^{n+1}\cdot(n+1)!}}{\frac{6n\cdot 3^n}{2^n\cdot n!}}}&|=\frac{6(n+1)\cdot 3^{n+1}\cdot 2^n\cdot n!}{2^{n+1}\cdot(n+1)!\cdot 6n\cdot 3^n}\\ \\
&\stackrel{\text{sortieren}}{=}\frac{6(n+1)}{6n}\cdot\frac{3^1\cdot 3^n\cdot 2^n}{3^n\cdot 2^1\cdot 2^n}\cdot \frac{n!}{n!\cdot(n+1)}=\underbrace{\frac{n+1}{n}}_{\ast^1}\cdot\underbrace{\frac{3}{2}}_{\ast^2}\cdot\underbrace{\frac{1}{n+1}}_{\ast^3}\\ \\
&\overset{n\to\infty}{\longrightarrow}1\cdot\frac{3}{2}\cdot 0=0<1
\end{align*}

Also konvergiert die Reihe (absolut).

$\ast^1$: Resultat aus dem ursprünglichen Polynom $6n$. In Zähler und Nenner: Polynom von gleichem Grad und gleichem Leitkoeffizient, Grenzwert ist 1.
$\ast^2$: Resultat aus den ursprünglichen Exponentialfkt. $3^n$ und $2^n$. Es verbleiben die Basen.
$\ast^2$: Resultat aus der ursprünglichen Fakultät $n!$ (im Nenner). Es verbleibt ein Polynom (im Nenner) mit Grad 1 (da $n!=(1\cdot n)!$). Dieser Term ist ausschlaggebend für den Grenzwert 0 (vgl. auch „wichtige Grenzwerte“ Formel).

Alternative (für alle, die es sehen): Wert ausrechnen!

Potenzreihen

Sogenannte Potenzreihen haben einen besonderen Aufbau:

\begin{align}
\sum_{k=0}^{\infty}{a_k}(x-x_0)^k
\end{align}

• $x_0$: Entwicklungspunkt
• $x$: variable Zahl aus $\mathbb{R}$
• wo $k$ beginnt ($k=0,1,2,\ldots$) ist egal

Bei diesen Reihen geht es darum, den Konvergenzradius R und damit das Intervall für $x$ zu bestimmen, für das die Reihe noch konvergiert: $x\in(x_0-R,x_0+R)$. Die Randbereiche müssen dann noch separat untersucht werden. Der Konvergenzradius $R$ kann entweder mit dem Quotienten- oder dem Wurzelkriterium folgendermaßen berechnet werden:

\begin{align}
\frac{1}{R} = \limsup\limits_{k\rightarrow\infty}{\left|\frac{a_{k+1}}{a_k}\right|} \quad \text{oder} \quad \frac{1}{R} = \limsup\limits_{k\rightarrow\infty}{\sqrt[k]{|{a_k}|}}
\end{align}

Der $\limsup$ ist sehr ähnlich dem gewöhnlichen limes: Es bedeutet lediglich „der größte Häufungspunkt“. Im Fall eines eindeutigen Grenzwertes ist es also äquivalent zum limes.

\begin{align*}
a_n&=\frac{2+(-1)^n}{4}\quad\quad\text{ Häufungspunkte sind } \frac{1}{4} \text{ und } \frac{3}{4}\\ \\
&{n\to\infty}{a_n}\text{ existiert nicht, aber }\limsup\limits_{n\rightarrow\infty} \ {a_n}=\frac{3}{4}
\end{align*}

Die Reihen Exponentialreihe sowie die Reihen der trigonometrischen Funktionen sind Potenzreihen mit Entwicklungspunkt $x_0=0$, $R=\infty$ und damit $x\in(-\infty,\infty)$. Die geometrische Reihe und deren Partialsumme ist eine Potenzreihe mit Entwicklungspunkt $x_0=0$, $R=1$ und damit $x\in(-1,1)$ (bzw. $q\in(-1,1)$).

Beispiel 1
\begin{align*}
\sum_{k=1}^{\infty}&{\left(\frac{(k+2)(x-2)}{2k}\right)^k}=\sum_{k=1}^{\infty}{\left(\frac{(k+2)}{2k}\right)^k\!\cdot (x-2)^k}=\sum_{k=1}^{\infty}{a_k\cdot (x-2)^k}\\ \\
&x_0=2 \text{ ist Entwicklungspunkt.}\\ \\
&\frac{1}{R}=\sqrt[k]{|{a_k}|}=\sqrt[k]{|{\left(\frac{k+2}{2k}\right)^k}|}=\frac{k+2}{2k}\overset{k\to\infty}{\frac{1}{2}}\\
\Rightarrow\ & R=2\ ,\quad x\in(2-2,2+2)=(0,4)\\ \\
&\text{Randbereich: }x=0: \text{ Da }\left(\frac{(k+2)(-2)}{2k}\right)^k=(-1)^k\cdot\left(\frac{k+2}{k}\right)^k\\ \\
&\text{ und } \left(\frac{k+2}{k}\right)^k\overset{k\to\infty}e^2 \text{ keine Nullfolge ist, divergiert die Reihe für }x=0\\ \\
&\text{Randbereich: }x=4: \text{ Da }\left(\frac{(k+2)(2)}{2k}\right)^k=\left(\frac{k+2}{k}\right)^k\overset{k\to\infty}{\longrightarrow}e^2\\ \\
&\text{keine Nullfolge ist, divergiert die Reihe für }x=4\\ \\
\Rightarrow & \text{ Für} x\in(0,4) \text{konvergiert die Reihe.}
\end{align*}

\begin{align*}
\sum_{k=0}^{\infty}&{\frac{kx^k}{k!}}=\sum_{k=0}^{\infty}{\frac{k}{k!}\cdot x^k}=\sum_{k=0}^{\infty}{a_k\cdot x^k}\\ \\
&x_0=0 \text{ ist Entwicklungspunkt.}\\ \\
&\frac{1}{R}=|{\frac{a_{k+1}}{a_k}|}=|{\frac{\frac{k+1}{(k+1)!}}{\frac{k}{k!}}}=\frac{(k+1)}{(k+1)!}\cdot \frac{k!}{k}=\frac{(k+1)\cdot 1}{(k+1)\cdot k}=\frac{1}{k}\overset{k\to\infty}{\longrightarrow}{0}\\ \\
\Rightarrow\ & R=\infty\ ,\quad x\in(- \infty,\infty) \ \Rightarrow \ \text{Für jedes } x\in\mathbb{R} \text{ konvergiert die Reihe.}
\end{align*}

Beispiel 2
\begin{align*}
\sum_{k=0}^{\infty}&{\frac{k^k(x+10)^k}{k!}}=\sum_{k=0}^{\infty}{\frac{k^k}{k!}\cdot (x+10)^k}=\sum_{k=0}^{\infty}{a_k\cdot (x+10)^k}\\ \\
&x_0=-10 \text{ ist Entwicklungspunkt.}\\ \\
&\frac{1}{R}= | {\frac{a_{k+1}}{a_k}}| = | \frac{ \frac{(k+1)^{k+1}}{(k+1)!}}{\frac{k^k}{k!}}| = \frac{(k+1)^1(k+1)^k}{(k+1)!} \cdot \frac{k}{k^k} = \frac{(k+1)^k}{k^k}=\left(1+\frac{1}{k}\right)^k\overset{k\to\infty}{\longrightarrow}{e}\\ \\
\Rightarrow\ & R=e^{-1} ,\quad x\in(-10-\text{e}^{-1},-10+e^{-1})\\ \\
\Rightarrow\ & \text{Für } x \in(-10-e^{-1},-10+e^{-1}) \text{ konvergiert die Reihe.}
\end{align*}

Beispiel 3
\begin{align*}
\sum_{k=1}^{\infty}&\frac{k^{2k}(x+1)^k}(k+1)!=\sum_{k=1}^{\infty}{\frac{k^{2k}}{(k+1)!}\cdot (x+1)^k}=\sum_{k=1}^{\infty}{a_k\cdot (x+1)^k}\\ \\
&x_0=-1 \text{ ist Entwicklungspunkt.}\\ \\
&\frac{1}{R}= | \frac{a_{k+1}}{a_k}| = | \frac{ \frac{(k+1)^{2k+2}}{(k+2)!}}{\frac{k^{2k}}{(k+1)!}}| = \frac{(k+1)^{2k+2}}{(k+2)!}\cdot \frac{(k+1)!}{k^{2k}}= \left(\frac{k+1}{k}\right)^{\!\!2k}\cdot\frac{(k+1)^2}{k+2}\\ \\
&\phantom{\frac{1}{R}}=\underbrace{\left(1+\frac{1}{k}\right)^{\!\!2k}}_{>1} \cdot \ \frac{k^2+2k+1}{k+2}\overset{k\to\infty}{\longrightarrow}{\infty}\\
\Rightarrow\ & R=0 ,\quad x\in(-1,-1)=\{\}\\ \\
&\text{Randbereich: }x=-1: \text{ Da } \sum_{k=1}^{\infty}{\frac{k^{2k}(-1+1)^k}{(k+1)!}}=\sum_{k=1}^{\infty}{\frac{k^{2k}0^k}{(k+1)!}}=0\\ \\
&\text{konvergiert die Reihe für }x = -1 \\ \\
\Rightarrow\ & \text{Nur für x=-1 konvergiert die Reihe.}
\end{align*}