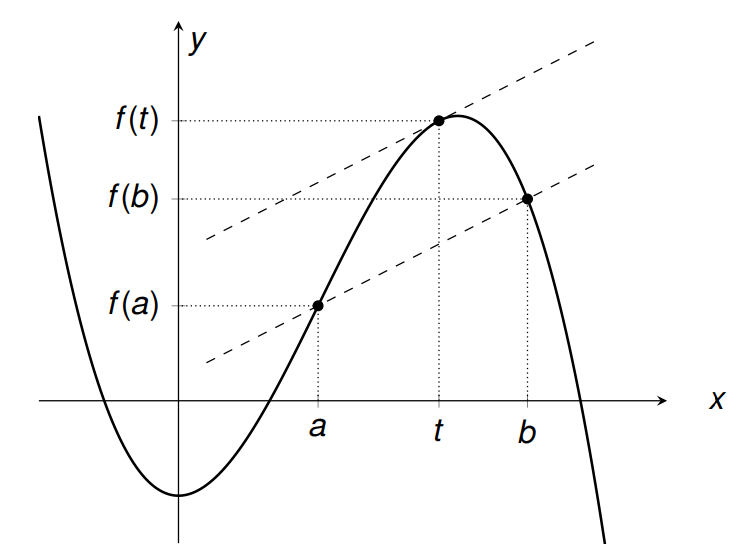
Der Mittelwertsatz

Wenn $f$ auf $(a,b)$ zusätzlich differenzierbar ist: Es gibt (mindestens) ein $t\in[a,b]$ für das die folgende Gleichung gilt:
\begin{align}
\frac{f(a)-f(b)}{a-b}=f'(t)
\end{align}

Anschaulich sagt der Satz aus, dass es (mindestens) eine Stelle in dem Intervall $[a,b]$ geben muss, an dem die Steigung des Graphen von $f$ gleich der Steigung der Sekante durch die Punkte $(a\,|\,f(a))$ und $(b\,|\,f(b))$ ist.