
Umkehrfunktion
Die Umkehrfunktion zur Funktion $f$ wird mit $f^{-1}$ notiert. ($f^{-1} \neq \frac{1}{f}$!).
$\quad f : D\longrightarrow W{\ldots}\notag$
$\quad f^{-1}:{x}\longrightarrow{W}{D}{\ldots}$
Definitions- und Wertebereich drehen sich um. $f^{-1}$ ordnet folglich jeder Zahl aus $W$ sein Urbild aus $D$ zu!
Es gilt:
$\quad (f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=f\Bigl(f^{-1}(x)\Bigr)=f^{-1}\Bigl(f(x)\Bigr)=x$
$\quad \text{bzw. } f\circ f^{-1}=f^{-1}\circ f=\text{id}_D$
Geometrisch ist deswegen auch der Graph von $f^{-1}$ die Spiegelung des Graphen von $f$ an der Winkelhalbierenden des ersten Quadranten im Koordinatenkreuz (die Winkelhalbierende entspricht dem Graphen der Identitätsfunktion ${id}_D:{D}\longrightarrow ,{id}_{D}(x)$, die jedes $x$ einfach auf sich selbst abbildet. Dies ist der Grund, warum Definitions- und Wertebereich gleich sind.)
Nachweis Injektivität
Am Einfachsten zeigen wir hierfür strenge Monotonie. Falls im Definitionsbereich der Funktion Lücken auftreten, so kann auch die Monotonie für die Teilintervalle bestimmt werden, danach muss jedoch weiter argumentiert werden, z.B. über das Grenzverhalten.
Vorausgesetzt die Funktion hat in $D$ keine Definitionslücke:
- Funktion ableiten (muss auf $D$ differenzierbar sein)
- Ableitung > 0 (evtl. vereinzelte Stellen $=0$ ) $\Rightarrow$ Funktion streng monoton wachsend auf $D$
- Ableitung < 0 (evtl. vereinzelte Stellen $=0$ ) $\Rightarrow$ Funktion streng monoton fallend auf $D$
Beispiel 1
Ist $f$ injektiv?
$f:{\mathbb{R}\setminus\{0\}}{\mathbb{R}}{\frac{x^2+3x+3}{x^3}}$
$f$ ist differenzierbar auf $\mathbb{R}\setminus\{0\}$, da es eine gebrochenrationale Funktion ist.
$f'(x)=\frac{(2x+3)x^3-(x^2+3x+3)\cdot 3x^2}{x^6}=\frac{(2x+3)x-(x^2+3x+3)\cdot 3}{x^4}$ $=\frac{-x^2-6x-9}{x^4}=-\frac{x^2+6x+9}{x^4}$
Nenner $x^4$ ist für alle $x\in\mathbb{R}\setminus\{0\}$ größer Null,
Zähler $x^2+6x+9$ stellt als Funktion eine nach oben geöffnete Parabel dar.
Nullstellen: $x_{1,2}=-3\pm\sqrt{3^2-9}=-3$ (doppelte Nullstelle). Also liegt der Scheitelpunkt auf der $x$-Achse.
Also ist auch $x^2+6x+9$ für alle $x\in\mathbb{R}\setminus\{-3,0\}$ größer Null und für $x=-3$ gleich Null (vereinzelte Stelle darf Null sein ($f$ hat hier eine Sattelstelle)). Damit also $-\frac{x^2+6x+9}{x^4}<0$ für alle $x\in\mathbb{R}\setminus\{0\}$.
$f$ fällt also jeweils streng monoton auf den Teilintervallen $(-\infty,0)$ und $(0,\infty)$.
Wenn jetzt $\lim\limits_{x \to -\infty}{f(x)}\leq \lim\limits_{x \to \infty}{f(x)}$ gilt und die Funktion die Grenzwerte für kein $x$ annimmt (so schließen wir das $„=“$ im $„\leq“$ für angenommene Funktionswerte aus, denn das darf bei Injektivität für Funktionswerte nicht gelten; für den Grenzwert ist das aber egal), muss $f$ injektiv sein.
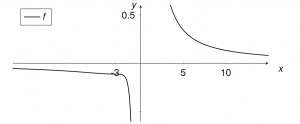
$\lim\limits_{x \to -\infty}{f(x)}=0$ und $\lim\limits_{x \to \infty}{f(x)}=0$ (Nennergrad $>$ Zählergrad)
$f(x)=0\ \Leftrightarrow\ x^2+3x+3=0\ \Leftrightarrow\ x_{1,2}=-\frac{3}{2}\pm\sqrt{\frac{9}{4}-\frac{12}{4}}$, negativer Term unter der Wurzel, also keine Lösung in $\mathbb{R}$.
Damit ist $f$ injektiv!
Nachweis Surjektivität
Für die Surjektivität gibt es kein allgemein gültiges Kochrezept.
Falls nicht explizit auf $x$ umgeformt werden kann „basteln“ wir uns den Nachweis über die Stetigkeit und dem Grenzverhalten der Funktion zusammen.
Um das Grenzverhalten festzustellen wird oft die Regel von l’hospital angewendet. Ebenfalls wird, wenn z.B. das Grenzverhalten einer Funktion $\infty$ für $x\rightarrow\pm\infty$ ist auf die Extremstellenberechnung zurückgreifen. Wo liegt dann der tiefste Punkt?
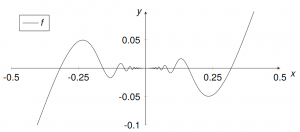
$f {:} \ \ \mathbb{R}\text{ \ {0}} \longrightarrow \mathbb{R}, \ f(x)={x^2\sin\left(\frac{1}{x}\right)} \quad \quad \text{ Ziel: Zeige, dass } f(\mathbb{R}\text{ \ {0}})=\mathbb{R}$ gilt.
$f$ ist auf ganz $\mathbb{R}\text{ \ {0}}$ stetig, da es aus stetigen Funktionen zusammengesetzt ist und kein unbestimmter Ausdruck auftreten kann (z.B. durch 0 teilen etc.)
Grenzverhalten:
\begin{align*}
&\lim\limits_{x \to \infty}{x^2\sin\left(\frac{1}{x}\right)}=“\infty\cdot 0″‚\ \Rightarrow\ \lim\limits_{x \to \infty}{\frac{\sin\left(\frac{1}{x}\right)}{\frac{1}{x^2}}}=“\frac{0}{0}“\\
\text{(l.’h.)}\Rightarrow\ &\lim\limits_{x \to \infty}{\frac{\cos\left(\frac{1}{x}\right)\cdot\left(-\frac{1}{x^2}\right)}{-2\cdot\frac{1}{x^3}}}=\frac{1}{2}\lim\limits_{x \to \infty}{\frac{\cos\left(\frac{1}{x}\right)}{\frac{1}{x}}}=\frac{1}{2}\lim\limits_{x \to \infty}{x\cdot\cos\left(\frac{1}{x}\right)}=\infty\text{ („$\infty\cdot 1$„)}\\[4mm]
&\lim\limits_{x \to – \infty}{x^2\sin\left(\frac{1}{x}\right)}=\ldots=\frac{1}{2}\lim\limits_{x \to – \infty}{x\cdot\cos\left(\frac{1}{x}\right)}=-\infty\text{ („$-\infty\cdot 1$“)}\\[4mm]
&\lim\limits_{x \to 0}{x^2\sin\left(\frac{1}{x}\right)}{=}0\text{ (da } x^2 \text{ gegen Null läuft und der Sinus beschränkt ist)}
\end{align*}
Wir wissen zu diesem Zeitpunkt schon, dass f auf jeden Fall alle Werte aus $(-\infty,0)\cup(0,\infty)$ annimmt:
$\quad$ Intervall $(-\infty,0)$ aufgrund von $\lim\limits_{x \to – \infty}{f(x)}, \lim\limits_{x \to 0}{f(x)}$ und Stetigkeit,
$\quad$ Intervall $(\infty,0)$ aufgrund von $\lim\limits_{x \to \infty}{f(x)}, \lim\limits_{x \to 0}{f(x)}$ und Stetigkeit.
Den Grenzwert 0 für $x\rightarrow 0$ können wir natürlich nicht als Funktionswert verwenden, da $x=0$ nicht im Definitionsbereich liegt. Jetzt können wir versuchen, einen $x$-Wert zu finden, für den $f(x)=0$ gilt: $x=\frac{1}{\pi}$ liefert das Gewünschte:
$f\left(\frac{1}{\pi}\right)=\frac{1}{\pi^2}\cdot\sin\left(\frac{1}{\frac{1}{\pi}}\right)=\frac{1}{\pi^2}\cdot\sin(\pi)=0$
(Wie kommen wir auf $\sin(\pi)=0$? $x^2$ wird nie Null, falls $x\neq 0$. Also muss der Sinus herhalten: Nullstellen des Sinus sind $\ldots-\pi, 0, \pi, 2\pi,\ldots$ und da im Sinus ein Kehrbruch steht, müssen wir die Nullstelle auch in einen Kehrbruch schreiben.)
Also gilt $f(\mathbb{R}\text{ \ {0}})=\mathbb{R}$ und damit ist $f$ surjektiv!
Bestimmung Umkehrfunktion
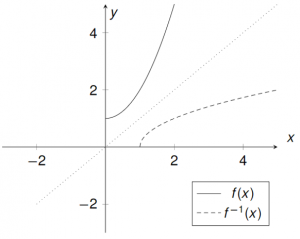
Wenn Bijektivität nachgewiesen wurde, kann ebenfalls die Umkehrvorschrift $f^{-1}(x)$ bestimmt werden (Achtung: nicht bei allen bijektiven Funktionen ist dies möglich!). Dafür muss $f(y)=x$ gesetzt und auf $y$ umgeformt werden:
\begin{align*}
\begin{array}{rrcl}
&f(y) = y^2+1&=&x\\
\Leftrightarrow\ &\quad y^2&=& x-1\\
\Leftrightarrow\ &\quad y&=&\sqrt{x-1} =: f^{-1}(x)\\
\Rightarrow\ &{f^{-1}} \ : \ {[1,\infty)}\longrightarrow {[0,\infty)}, \ f^{-1}(x)={\sqrt{x-1}}
\end{array}
\end{align*}
Kombiniertes Beispiel:
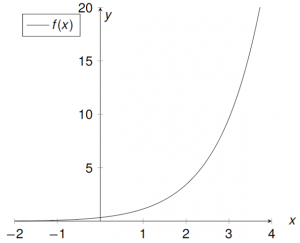
$f: \ \mathbb{R} \longrightarrow {(0,\infty)}\ f(x) \ =\frac{e^x}{e^{-x}+2}$
Injektivität
- $f$ besitzt keine Polstellen, da Nenner nie Null wird ($e^{-x}+2>0$ für alle $x\in\mathbb{R}$).
- $f$ ist auf ganz $\mathbb{R}$ differenzierbar.
- Ableiten:
\begin{align*}&f'(x)=\frac{\exp^{x}(\exp^{-x}+2)-\text{e}^{x}(-\exp^{-x})}{(\exp^{-x}+2)^2}=\frac{1+2\exp^{x}+1}{(\exp^{-x}+2)^2}=2\cdot\frac{\exp^{x}+1}{(\exp^{-x}+2)^2}
\end{align*}
$f'(x)>0$ für alle $x\in\mathbb{R}$. Damit ist $f$ streng monoton steigend und deshalb injektiv.
Surjektivität
- $f$ ist stetig, da aus stetigen Funktionen zusammengesetzt.
- $\lim\limits_{x\to \infty}{f(x)}=0\ ,\ \lim\limits_{x\to \infty}=\infty$
Der ganze Wertebereich wird von $f(x)$ erreicht und damit ist $f$ surjektiv.
$f$ ist also bijektiv und besitzt daher eine Umkehrfunktion $f^{-1}$
${f^{-1}}{x}{(0,\infty)}\mathbb{R}{\ldots}$\begin{align*}
&&f(y) = \frac{\exp^y}{\exp^{-y}+2}&=x\quad\left|\right.\text{ Bruch erweitern mit }\exp^y\\ \\
\Leftrightarrow\ &&\quad \frac{\exp^{2y}}{1+2\exp^y}&= x\\ \\
\Leftrightarrow\ &&\quad \exp^{2y}-2x\exp^y-x&= 0\\ \\
\Leftrightarrow\ &&\quad \exp^y_{1,2}&= x\pm\sqrt{x^2+x}\stackrel{!}{>}0\quad \text{da} \exp^y>0\ \forall y\in\mathbb{R}\\ \\
\Leftrightarrow\ &&\quad \exp^y&= x+\sqrt{x^2+x}\\ \\
\Leftrightarrow\ &&\quad y&= \ln\left(x+\sqrt{x^2+x}\right)=:f^{-1}(x)\\ \\ \\
\Rightarrow\ &&\quad {f^{-1}}:{(0,\infty)}\rightarrow\mathbb{R}, {f^{-1}}(x)={\ln\left(x+\sqrt{x^2+x}\right)}
\end{align*}