
Differentialgleichung
Eine Differentialgleichung (kurz Diff.’gleichung oder DGL) ist eine Gleichung, in der eine Funktion und auch Ableitungen von dieser Funktion auftauchen können. Die Lösung dieser Art von Gleichung ist eine Funktion – keine Zahl!
Inhalte auf dieser Seite
- Notationen von Differentialgleichungen
- Typisierung von Differentialgleichungen
- Übergeordnete Lösungsansätze
- Beispiele: Lineare Differentialgleichungen erster Ordnung
- Beispiele: Lineare DGL höherer Ordnung mit konstanten Koeffizienten
- Beispiele: Nicht-lineare DGL erster Ordnung
- Bernoulli-Differentialgleichung
- Koordinatenebenen
Notationen von Differentialgleichungen
Zunächst wollen wir hier kurz klären, in welchen Schreibweisen Differentialgleichungen auftreten können.
Funktion mit und ohne Funktionsargument
Je nach Mathematik Veranstaltung, Büchern oder Internetquellen, kann die Funktion in der DGL mit und ohne Funktionsargument notiert sein.
Beispiel
\begin{alignat*}{3}
&\text{Ohne Funktionsargument:}\quad & ~&&2y’+yx&=0\\
&\text{Mit Funktionsargument:}\quad &\quad&&2y'(x)+y(x)x&=0
\end{alignat*}
Im Fall ohne Funktionsargument erkennen wir die Funktion daran, welche der Variablen eine Ableitungskennzeichnung enthält (im Beispiel oben das $y$, da $y‘$ auftaucht). Die andere Variable ist dann die Variable, von der die Funktion abhängt (Im Beispiel oben das $x$).
Tipp
Im Folgenden werden wir bei der Funktion nicht mit dazu schreiben, von welcher Variable diese abhängt. Diese Notation stellt den Standard in den allermeisten Veranstaltungen dar und du solltest dich daran gewöhnen.
Notation der Ableitungsterme
Im Allgemeinen solltest du wissen, dass Folgendes gilt:
\begin{align}
&y^{(n)}\quad\text{$n$-te Ableitung der Funktion $y$} \label{eq:allgemeineableitungsnotation}
\end{align}
Verwechsle in diesem Zuge auf keinen Fall das Folgende:
\begin{align*}
y^{(2)}=y“\quad \neq\quad y^2=y\cdot y
\end{align*}
Oftmals (besonders im Ingenieurbereich) wirst du bei Differentialgleichungen Ableitungen wie $\dot y$ anstatt $y‘$ sehen. Das bedeutet lediglich, dass die Variable die Zeit $t$ ist und $\dot y$ die Ableitung nach der Zeit darstellt:
\begin{align*}
y(t),\quad \frac{dy}{dt}(t)=\dot y(t),\quad \frac{d^2y}{dt^2}(t)=\ddot y(t),\quad\ldots
\end{align*}
Implizite und explizite Darstellung
Die explizite Darstellung einer DGL erhalten wir, wenn wir die DGL auf die höchste vorkommende Ableitung umstellen können. Falls das nicht möglich ist, kann die DGL nur in impliziter Darstellung geschrieben werden.
\begin{align*}
&\text{DGL 1: Implizite und explizite Darstellung:}\quad 2y’+yx=0\quad y’=-\frac{1}{2}yx\\
&\text{DGL 2: Implizite Darstellung:}\quad y’+ e^{y‘}=y\quad\text{(nicht auf $y‘$ auflösbar)}
\end{align*}
Abstrakte Notation durch „übergeordnete“ Funktion
Manchmal ist es hilfreich (z.B. um Begriffe sauber zu definieren), die DGL als „übergeordnete“ Funktion zu deklarieren ($f$ für explizite Darstellung und $F$ für implizite Darstellung). Diese hängt dann von den Variablen und der gesuchten Funktion samt ihren Ableitungen ab (recht abstrakte Notation):
\begin{align}
\text{In expliziter Form:}\quad & y^{(n)}=f(x,y,y‘,y“,\ldots,y^{(n-1)})\label{eq:dglinfunktionsschreibweiseexplizit}\\
\text{In impliziter Form:}\quad & 0=F(x,y,y‘,y“,\ldots,y^{(n-1)},y^{(n)})\label{eq:dglinfunktionsschreibweiseimplizit}
\end{align}
\begin{alignat*}{3}
&\text{DGL 1:}\quad&&2y’+yx=0&\quad y’=-\frac{1}{2}yx=:f(x,y)\\[2mm]
&\text{DGL 2:d}\quad&&y’+ e^{y‘}=y& \quad 0=y-y‘- e^{y‘}=:F(x,y,y‘)
\end{alignat*}
Notation innerhalb dieses Buchs
Wir werden uns in diesem gesamten Kapitel darauf einigen, dass in den DGLs $y$ die gesuchte Funktion darstellt, $x$ die Variable ist und daher auch ‚ die Ableitung kennzeichnet.
Typisierung von Differentialgleichungen
Dieses Unterkapitel stellt im ersten Schritt das wichtigste Kapitel dar. Ohne eine vorliegende DGL korrekt zu typisieren, werden wir kein geeignetes Verfahren auswählen können, um Lösungen der DGL zu bestimmen. Außerdem ordnen wir zu der Typisierung auch die Begrifflichkeiten von Lösungsvarianten zu.
Typisierung der DGL
Zur Einführung hier für dich eine kleine Übersicht für die Strukturierung der Typisierung. Das „`Baumdiagramm“‚ sollte selbsterklärend sein.
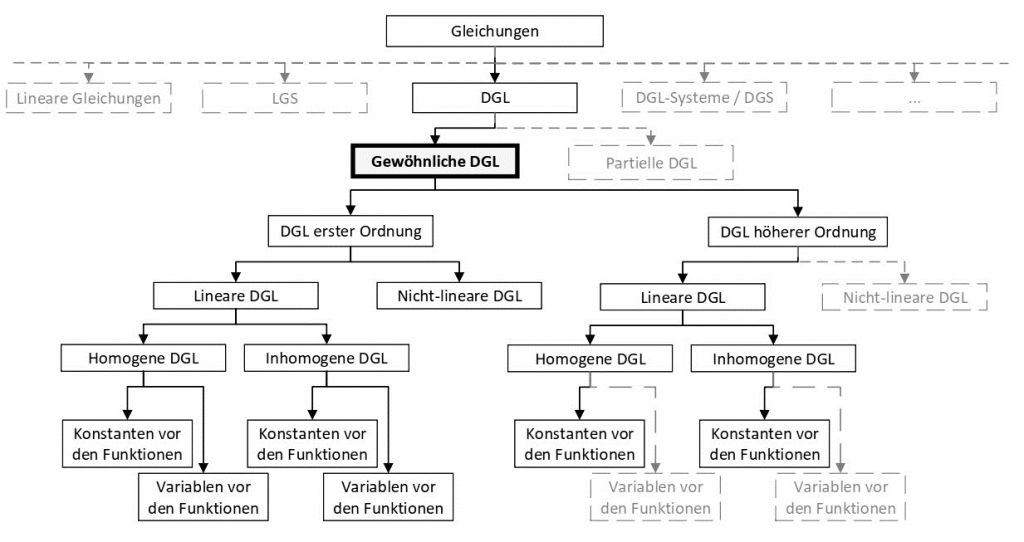
Die grau gestrichelten Typisierungen in der Übersicht werden wir in diesem Artikel nicht behandeln.
Die grundlegendste Typisierung einer DGL erhalten wir, wenn wir uns anschauen, von wie vielen Variablen die gesuchte Funktion abhängt bzw. ob partielle Ableitungen der Funktion in der DGL auftauchen.
- Gewöhnliche DGL: Die gesuchte Funktion hängt lediglich von einer Variable ab bzw. es tauchen nur Ableitungen nach einer Variablen auf.
- Partielle DGL: Die gesuchte Funktion hängt von mehreren Variablen ab und es tauchen partielle Ableitungen der Funktion auf.
\begin{alignat*}{2}
& \text{Gewöhnliche DGL: }&y(x)+2y'(x)&=\sin(x)\\
& \text{Partielle DGL: }&2y(x,t)+\frac{\partial y}{\partial x}(x,t)+3\frac{\partial y}{\partial t}(x,t)&=0
\end{alignat*}
Wir werden hier ausschließlich gewöhnliche DGLs behandeln. Jegliche Notationen und Beispiele beziehen sich in diesem gesamten Kapitel also auf gewöhnliche DGLs.
Differentialgleichung erster, oder höherer, Ordnung
Die nächste, wichtige Typisierung ist die Ordnung der DGL. Darunter verstehen wir die höchste auftauchende Ableitung von $y$.
- DGL erster Ordnung: In der DGL ist die höchste Ableitung der gesuchten Funktion ihre erste Ableitung, also $f(x,y,y‘)=0$.
- DGL höherer ($n$-ter) Ordnung: In der DGL tauchen Ableitung der gesuchten Funktion bis zur $n$-ten Ableitung auf, also $f(x,y,y‘,y“,\ldots,y^{(n)})=0$.
Lineare oder nicht-lineare Differentialgleichungen
Eine ebenso wichtige Unterteilung von DGLs ist, ob diese linear oder nicht-linear sind. Falls eine DGL linear ist, hat sie die folgende Form:
\begin{align}
&y^{(n)}+a_{n-1}(x)\cdot y^{(n-1)}+\ldots+a_2(x)\cdot y“+a_1(x)\cdot y’+a_0(x)\cdot y=b(x)
\end{align}
..andernfalls ist sie nicht linear.
Dass vor $\pmb{y^{(n)}}$ kein $\pmb{a_n(x)}$ steht, ist kein Fehler, denn für spätere Lösungsverfahren ist es wichtig, dass dort eine 1 steht. Falls das in einer Aufgabe nicht der Fall sein sollte, können wir durch den Faktor vor dem $\pmb{y^{(n)}}$ teilen, um auf die lineare Gestalt zu kommen.
Homogene oder inhomogene (lineare) Differentialgeichungen
Diese Unterteilung existiert nur für lineare DGLs! Also ausgehend von der Form $amp;y^{(n)}+a_{n-1}(x)\cdot y^{(n-1)}+\ldots+a_2(x)\cdot y“+a_1(x)\cdot y’+a_0(x)\cdot y=b(x)$ gilt:
- Homogene DGL: $b(x)=0$
- Inhomogene DGL: $b(x)\neq 0$
\begin{alignat*}{2}
%& \text{Homogene DGL: }&y+xy’&=0\\
%& \text{Inhomogene DGL: }&y+xy’&=\sin(x)\quad\text{oder}\quad y+xy‘-\sin(x)=0
\end{alignat*}
An welcher Stelle der Term $\pmb{b(x)}$ als Summand in der DGL steht, spielt keine Rolle!
$\pmb{b(x)}$ wird auch Störfunktion/-term genannt.
Koeffizient oder variabler Term als Faktor vor den Funktionen in (linearer) DGL
Diese Unterteilung existiert nur für lineare DGLs! Also wieder ausgehend von der linearen Form gilt:
- Koeffizient als Faktor vor den Funktionen: $a_{0,\ldots,n-1}(x)$ sind Zahlen aus $\mathbb{R}$. Also:
\begin{align}
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=b(x)
\end{align} - Variabler Term als Faktor vor den Funktionen: Mindestens einer der Terme $a_{0,\ldots,n-1}(x)$ hängt von $x$ ab.
Autonome und nicht-autonome DGL
In vielen Büchern und Skripten taucht die Typisierung autonome DGL auf. Eine DGL heißt autonom, wenn die Variable $x$ nicht explizit in der DGL auftaucht (also lediglich versteckt als Funktions\-argument in der Funktion $y$ und deren Ableitungen):
\begin{align}
\text{Autonome DGL:}\quad& y^{(n)}=f(y,y‘,\ldots,y^{(n-1)})\text{ bzw. } 0=F(y,y‘,\ldots,y^{(n-1)},y^{(n)})\\
\text{Nicht-autonome DGL:}\quad& y^{(n)}=f(x,y,y‘,\ldots,y^{(n-1)})\text{ bzw. } 0=F(x,y,y‘,\ldots,y^{(n-1)},y^{(n)})
\end{align}
Warum taucht die Unterteilung in unserem Baumdiagramm nicht auf? Weil diese Typisierung nicht zwischen homogen und inhomogen bei linearen DGLs unterscheidet und wir daher lieber auf „homogen“-„inhomogen“ sowie „Konstanten vor den Funktionen“-„Variablen vor den Funktionen“ zurückgreifen.
Eine homogene lineare DGL mit Konstanten vor den Funktionen ist auf jeden Fall eine autonome DGL. Inhomogene lineare DGLs und nicht-lineare DGLs können entweder autonom oder nicht-autonom sein.
\begin{align*}
\text{Autonome DGL:}\quad y’&=2y+6 \\
y“&=3y‘-y \\
y’&=y^3+y \\
\text{Nicht-autonome DGL:}\quad y’&=xy \\
y’&=y+\sin(x) \\
y’&=x e^y+1
\end{align*}
Gekoppelte oder entkoppelte Differentialgleichungen
Diese Typisierung existiert lediglich bei Differentialgleichungssystemen (DGL-Systeme bzw. DGS), also bei mehreren DGLs, die zusammen gelöst werden sollen.
Beispiele gewöhnlicher DGLs mit Typisierungen
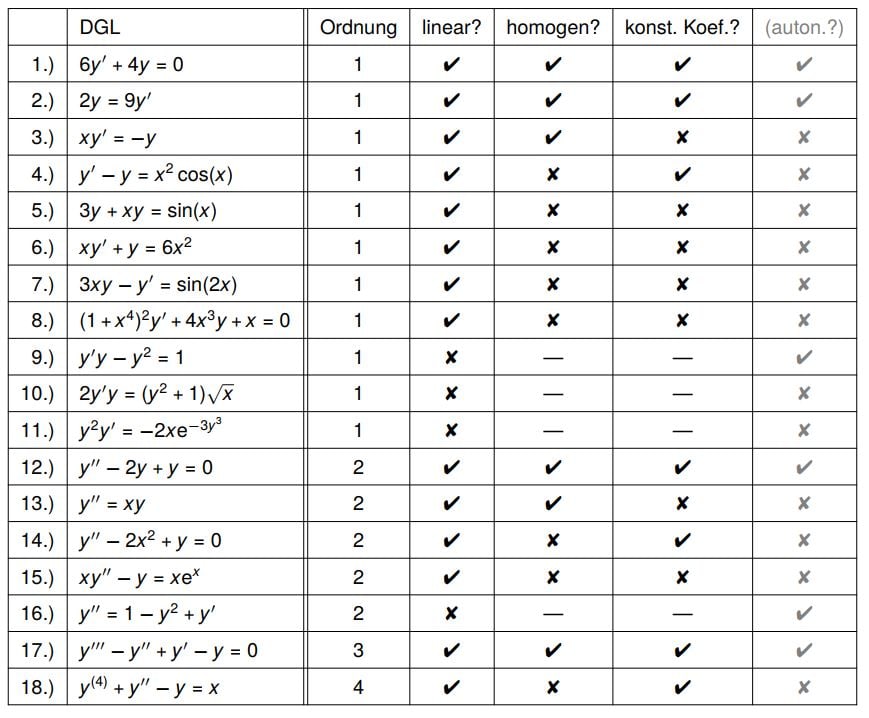
Typisierung der Lösungsvarianten
Du wirst in den folgenden Unterkapiteln, und auch in deiner Lehrveranstaltung und Prüfung, auf verschiedene Begriffe für Lösungen einer Differentialgleichung stoßen. Die Folgenden solltest du in den Gesamtzusammenhang richtig einordnen- und bestimmen können.
Homogene Lösung
Wird als $y_0$, $y_{hom}$ oder $y_h$ betitelt. Das sind alle Lösungen einer homogenen Differentialgleichung.
Partikuläre Lösung
Diese wird meistens mit $y_{part}$ oder $y_p$ bezeichnet. Ganz allgemein ist das eine Funktion, die die Differentialgleichung löst.
Manchmal wird die partikuläre Lösung auch spezielle Lösung genannt.
Allgemeine Lösung einer inhomogenen Differentialgleichung
Die allgemeine Lösung einer inhomogenen Differentialgleichung wird $y_{allg}$ oder einfach ohne Index $y$ genannt und beinhaltet alle Lösungen der DGL. Sie hängt von einer oder mehreren, frei wählbaren Konstanten ab. Sie ist die Summe aus homogener und partikulärer Lösung einer DGL, also:
\begin{align}
&y_{allg}=y_h+y_p
\end{align}
Du kannst dir hier die Analogie heranziehen, dass die Lösungen einer inhomogenen DGL auf einer Geraden/Ebene liegen und die Parameterdarstellung dieser Geraden ist – mit $y_h$ als Richtungsvektor (mit variablem Parameter) und $y_p$ als Ortsvektor (irgendein Punkt auf der Geraden / ein Vektor, der die Gerade aus dem Ursprung heraus schiebt).
Spezielle & Explizite Lösung
Das ist die Lösung einer DGL, die konkret vorgegebenen Anfangs-/Randwerten genügt (also die Lösung des AWP/RWP, $y_{spez}$). Diese Lösung bestimmen wir für gewöhnlich aus der allgemeinen Lösung einer DGL, indem wir die dort auftauchenden und noch nicht näher bestimmten Konstanten aus den Anfangs-/Randwerten ermitteln.
In Analogie zur Anmerkung davor wäre $y_{spez}$ nun ein spezieller Punkt auf der Geraden/Ebene (Parameter vor dem Richtungsvektor erhält konkrete Werte).
Fundamentalsystem/-basis
Ein Fundamentalsystem (FS) ist keine Lösung im eigentlichen Sinne, aber ein sehr wichtiger Begriff, der in dieses Unterkapitel passt!
Ein Fundamentalsystem (auch Hauptsystem genannt) ist eine Basis des Vektorraums, der aus der Menge aller Lösungen eines homogenen, gewöhnlichen Differentialgleichungssystems. (vgl. Walter, W.: Gewöhnliche Differentialgleichungen. Springer-Verlag Berlin, 2000)
Für dieses Buch: In einem FS befinden sich also linear unabhängige Lösungen einer homogenen linearen gewöhnlichen DGL. Wir notieren hier ganz allgemein:
\begin{align}
& \text{FS}=\left\{y_1,\ y_2,\ \ldots,\ y_n\right\}
\end{align}
Übergeordnete Lösungsansätze
Einordnung von Lösungsansätzen
Das folgende Diagramm zeigt auf, welche Lösungsansätze du wann verwenden solltest. Falls mehrere Lösungswege möglich sind, haben wir diese in unserer präferierten Reihenfolge notiert.
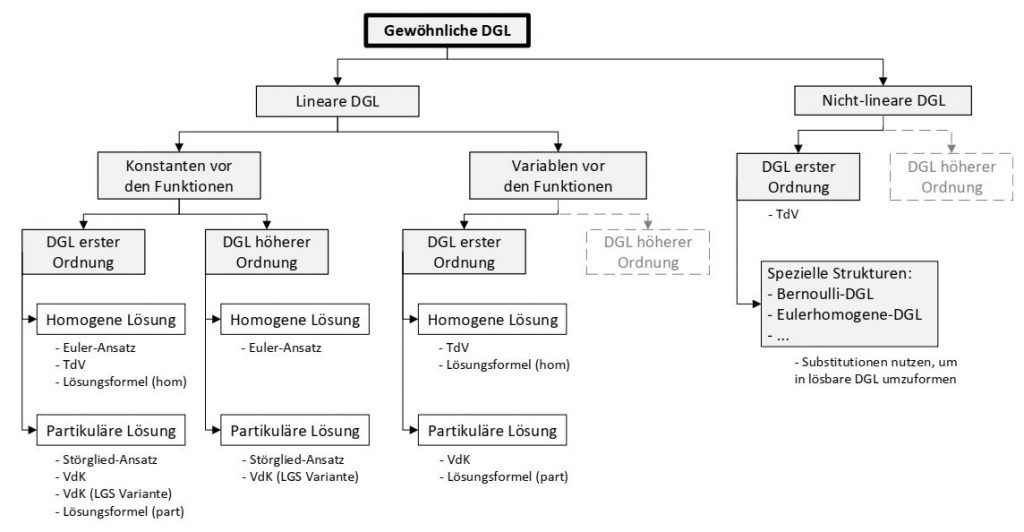
Beachte: Partikuläre Lösungen können sich – je nachdem, welchen Lösungsansatz wir wählen – voneinander unterscheiden!
TdV – Trennung der Variablen / Trennung der Veränderlichen
Mit der Methode TdV können wir die homogene Lösung einer linearen DGL erster Ordnung (und falls es möglich ist, auch die Lösung einer nicht-linearen DGL erster Ordnung) ermitteln. Voraussetzung ist, dass die DGL in expliziter Darstellung separierbar ist (d.h. dass die Variablen $y$ und $x$ getrennt werden können):
\begin{align}
\text{Separierbare DGL:}\quad & y’= (\text{„Term hängt nur von x ab“})\cdot(\text{„Term hängt nur von y ab“})
\end{align}
Beispiel
\begin{alignat*}{2}
y’+2xy&=0&&\quad y’=(-2x)\cdot(y)\\
y^2y’+2x&=0&&\quad y’=(-2x)\cdot\left(\frac{1}{y^2}\right)\\
xy‘-3y&=0&&\quad y’=\left(\frac{3}{x}\right)\cdot(y)\\
y’&=2x-xy&&\ y’=(x)\cdot(2-y)
\end{alignat*}
Die letzte DGL stellt eine Ausnahme bzgl. der Lösungsmethoden-Übersicht dar, da diese eine inhomogene lineare DGL 1. Ordnung ist. Wenn wir erkennen, dass eine inhomogene DGL separierbar ist, brauchen wir nicht über den Weg der Formel gehen, sondern können die inhomogene DGL direkt per TdV lösen.
Verfahren
- DGL korrekt typisieren
- Wir schreiben die Ableitung $y’$ in Folgendes um:
\begin{align}
y’&=\frac{dy}{dx}
\end{align} - Jetzt trennen wir die Variablen. Wir bringen alle Terme mit $y$ auf die linke Seite und alle Terme mit $x$ auf die rechte Seite der Gleichung. Dabei muss das $dy$ und $dx$ im Zähler stehen:\begin{align}
& (\text{„Term hängt nur von $y$ ab“})\cdot dy = (\text{„Term hängt nur von $x$ ab“})\cdot dx
\end{align}Wir können die DGL auch erst in Form bringen, dann mit $dx$ multiplizieren und durch den „von $x$ abhängigen Term“ teilen.
Empfehlung: Bringe konstante Faktoren auf die rechte Seite. So musst du nachher die „$+C$“ nicht unnötig umbenennen usw. - Beide Seiten integrieren:
\begin{align}
& \int(\text{„Term hängt nur von $y$ ab“})\cdot dy = \int(\text{„Term hängt nur von $x$ ab“})\cdot dx
\end{align}Dabei benötigen wir nur bei einem der beiden Integrale (bei der von $x$ abhängigen Seite) die „$+$ Konstante“ am Ende.
- Auf $y$ auflösen.
Die größte Schwierigkeit besteht hier meistens beim Integrieren der Terme (Punkt 3), besonders wenn wir nicht-lineare DGLs per TdV lösen wollen.
Ist ein AWP/RWP gegeben und wir wollen direkt die explizite Lösung bestimmen, können wir bei Punkt 4 alternativ einsteigen:
- Beide Seiten folgendermaßen integrieren: Wenn das AWP/RWP $y(x_0)=y_0$ gegeben ist, dann:\begin{align}
& \int_{y_0}^y(\text{„Term hängt nur von $y$ ab“})\cdot dy = \int_{x_0}^x(\text{„Term hängt nur von $x$ ab“})\cdot dx
\end{align} - Auf $y$ auflösen. Damit ist das $y=y_{spez}$
Durch diesen Weg ermitteln wir nicht die allgemeine Lösung der DGL!
Euler-Ansatz
Mit dem Euler-Ansatz geben wir die grundsätzliche Struktur der homogenen Lösung einer linearen Differentialgleichung mit konstanten Koeffizienten vor und setzen diesen in die DGL ein.
Der Ansatz lautet wie folgt:
\begin{align}
&y:= e^{\lambda x}
\end{align}
Die Ableitungen dazu sind dann natürlich:
\begin{align}
&\left(y=e^{\lambda x}\right),\quad y’=\lambda e^{\lambda x},\quad y“=\lambda^2 e^{\lambda x},\quad y“’=\lambda^3 e^{\lambda x},\quad\ldots
\end{align}
Die Terme aus dem Ansatz und der Ableitung in $y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=b(x)$ eingesetzt ergibt
\begin{align}
&\lambda^n e^{\lambda x}+\ldots+a_2\cdot \lambda^2 e^{\lambda x}+a_1\cdot \lambda e^{\lambda x}+a_0\cdot e^{\lambda x}=0\quad\Bigl|\Bigr.\ : e^{\lambda x}\quad(e^{\lambda x}>0\ \forall\,\lambda,x\in\mathbb{R})\notag\\
\Rightarrow\ & \underbrace{\underbrace{\lambda^n+\ldots+a_2\cdot \lambda^2+a_1\cdot \lambda+a_0}_{\text{charakteristisches Polynom}}=0}_{\text{charakteristische Gleichung}}
\end{align}
- DGL korrekt typisieren.
- Charakteristische Gleichung der DGL bestimmen.
- Nullstellen des charakteristisch. Polynoms bestimmen (die charakteristische Gleichung lösen).
- In Abhängigkeit dieser Nullstellen ein (Lösungs-)Fundamentalsystem (FS) aufstellen:$\bullet$ Die Nullstellen ($\lambda_{1,\ldots,n}$) sind alle reell und alle voneinander unterschiedlich:
\begin{align}
& \text{FS}=\left\{e^{\lambda_1 x},\ e^{\lambda_2 x},\ldots,e^{\lambda_n x}\right\}
\end{align}
$\bullet$ Unter den Nullstellen tauchen komplex konjugierte Paare ($\lambda=a\pm bi$) auf:
\begin{align}
& \text{FS}=\left\{\ldots,\ e^{ax}\cos(bx),\ e^{ax}\sin(bx),\ \ldots\right\}
\end{align}
$\bullet$ Nullstelle $\lambda$ (reell bzw. komplex konjugiertes Paar $\lambda=a+bi$) taucht mehrfach ($n$-mal) auf:
\begin{align}
& \text{FS}=\left\{\ldots,\ e^{\lambda x},\ x e^{\lambda x},\ \ldots,\ x^{n-1} e^{\lambda x},\ldots\right\}\quad\text{bzw.}\\
& \text{FS}=\left\{\ldots,\ e^{ax}\cos(bx),\ e^{ax}\sin(bx),\ x e^{ax}\cos(bx),\ x e^{ax}\sin(bx),\ldots,\right.\\
&\qquad\qquad\quad\; x^{n-1} e^{ax}\cos(bx),\ x^{n-1} e^{ax}\sin(bx),\ ,\ldots\left.\right\}
\end{align} - Für die Lösung $y_h$ alle Elemente des Fundamentalsystems mit jeweils einer Konstanten ($C_1$, $C_2$, \ldots) multiplizieren und danach alles addieren. Anders (als Zeilen- mal Spaltenvektor) notiert:
\begin{align}
& y_h=(\text{FS})\cdot{(C_1,\ C_2,\ C_3,\ \ldots)}
\end{align}
Wir spannen hier sozusagen den Lösungsraum auf, wie die lineare Hülle bei Vektoren!
Beispiele zum Aufstellen vom FS und Bestimmen von $y_h$:
\begin{align*}
\ldots\quad\lambda_1=-2,\ \lambda_2=1,\ \lambda_3=4
\text{FS}=\left\{e^{-2x},e^{1x},e^{4x}\right\}=\left\{e^{-2x},e^{x},e^{4x}\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_{h}=C_1e^{-2x}+C_2 e^{x}+C_3 e^{4x}
\end{align*}
\begin{align*}
\ldots\quad\lambda_1=0,\ \lambda_2=2,\ \lambda_3=2,\ \lambda_4=2
\end{align*}
\begin{align*}
\text{FS}=\left\{e^{0x},e^{2x},x^1 e^{2x},x^2 e^{2x}\right\}=\left\{1, e^{2x},x e^{2x},x^2 e^{2x}\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_{h}=C_1\cdot 1+C_2 e^{2x}+C_3x e^{2x}+C_4x^2 e^{2x}=C_1+C_2 e^{2x}+C_3x e^{2x}+C_4x^2 e^{2x}
\end{align*}
\begin{align*}
\ldots\quad\lambda_1=-1,\ \lambda_2=1,\ \lambda_{3,4}=2\pm 3i
\end{align*}
\begin{align*}
\text{FS}=\left\{e^{-1x}, e^{1x}, e^{2x}\cos(3x), e^{2x}\sin(3x)\right\}=\left\{e^{-x},e^{x},e^{2x}\cos(3x),e^{2x}\sin(3x)\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_{h}=C_1 e^{-x}+C_2 e^{x}+C_3 e^{x}\cos(3x)+C_4 e^{2x}\sin(3x)
\end{align*}
\begin{align*}
\ldots\quad\lambda_1=0,\ \lambda_2=0,\ \lambda_{3,4}=1\pm 3i,\ \lambda_{5,6}=1\pm 3i
\end{align*}
\begin{align*}
\text{FS}&=\left\{e^{0x},x^1 e^{0x},e^{1x}\cos(3x),e^{1x}\sin(3x),x^1 e^{1x}\cos(3x),x^1 e^{1x}\sin(3x)\right\}\\
&=\left\{1,x, e^{x}\cos(3x), e^{x}\sin(3x),x e^{x}\cos(3x),x e^{x}\sin(3x)\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_{h}&=C_1\cdot 1+C_2x+C_3 e^{x}\cos(3x)+C_4 e^{x}\sin(3x)+C_5x e^{x}\cos(3x)+C_6x e^{x}\sin(3x)\\
&=C_1+C_2x+C_3 e^{x}\cos(3x)+C_4 e^{x}\sin(3x)+C_5x e^{x}\cos(3x)+C_6x e^{x}\sin(3x)
\end{align*}
$y_h$: Lösungsformel (hom)
Wenn wir unsere DGL richtig typisiert haben, können wir eine homogene lineare DGL erster Ordnung in expliziter Form folgendermaßen schreiben:
\begin{align}
y’=a_0(x)y
\end{align}
- DGL korrekt typisieren.
- DGL in Form $y’=a_0(x)y$ bringen.
- Lösung ist gegeben durch:
\begin{align}
y&=C\cdot e^{A_0(x)}\quad\text{mit}\quad A_0(x)=\int{a_0(x)}dx\quad\text{und}\quad C\in\mathbb{R}
\end{align}
Denn der allgemeine Ablauf der TdV läuft bei homogenen linearen DGLs erster Ordnung immer auf diese Lösungsform hinaus!
Bei $\int{a_0(x)}dx$ ist die „$+$ Konstante“ am Ende des unbestimmten Integrals nicht nötig!
Superposition von partikulären Lösungen
Bevor wir zu Lösungsmethoden für partikuläre Lösungen kommen, wollen wir hier das Folgende klären:
Wenn der inhomogene Teil (das Störglied) einer DGL eine Summe aus einzelnen Störgliedern ist ($b(x)=b_1(x)+b_2(x)+\ldots$), dann können wir zu jedem der Summanden eine eigene partikuläre Lösung finden und diese für die ursprüngliche DGL wieder aufaddieren:
Gegeben ist eine DGL
\begin{align}
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=\underbrace{b_1(x)+b_2(x)+\ldots}_{b(x)}\label{eq:dglfuersuperposition}
\end{align}
Suche partikuläre Lösungen $y_{p,1}$, $y_{p,2}$, … für die DGLs
\begin{align*}
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=b_1(x)\\
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=b_2(x)\\
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=\ldots
\end{align*}
Dann ist die gesamte partikuläre Lösung für das vorgegeben DGL durch die Addition der einzelnen partikulären Lösungen gegeben:
\begin{align}
& y_p=y_{p,1}+y_{p,2}+\ldots
\end{align}
$y_p$: Störgliedansatz
Mit einem Störgliedansatz geben wir unserer Ansatzfunktion $y_p$ eine allgemeine Struktur nach Art des Störglieds $b(x)$ vor. Dies gilt für DGLs der Art:
\begin{align*}
&y^{(n)}+a_{n-1}\cdot y^{(n-1)}+\ldots+a_2\cdot y“+a_1\cdot y’+a_0\cdot y=b(x)
\end{align*}
Die Störgliedansätze beinhalten Parameter, die wir durch das Einsetzen in die DGL am Ende bestimmen müssen.
Nicht immer können wir $y_p$ durch einen Störgliedansatz ermitteln. Wenn es aber geht ist es unserer Meinung nach der schnellste und beste Rechenweg.
Es existieren in Fachliteratur und auf Internetseiten dutzende Tabellen, die uns mögliche Ansätze liefern. Manche sind allgemeiner gehalten, manche enthalten vermeintlich etliche Sonderfälle. Wir haben versucht, das Ganze — so gut es geht — leicht verständlich zu beschreiben.
Du solltest im Vorfeld die homogene Lösung deiner DGL mit dem Euler-Ansatz gelöst haben. Die allgemeine Ansatztabelle für $y_p$:
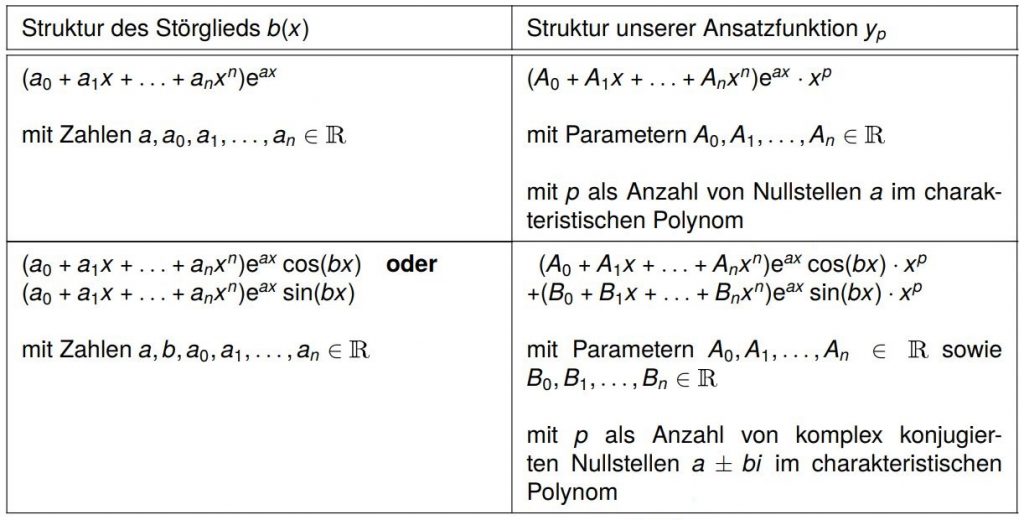
In der Struktur des Störglieds steht dabei das Polynom $(a_0+a_1x+\ldots+a_nx^n)$ vom Grad $n$. Das bedeutet für den Störgliedansatz, dass ein allgemeines Polynom $(A_0+A_1x+\ldots+A_nx^n)$ bis genau zu diesem Grad angesetzt werden muss.
Das Auftauchen des Terms $x^p$ im Störgliedansatz nennen wir auch „Resonanzfall“. In der Tabelle ist $p$ beschrieben als die Anzahl der Nullstellen im char. Polynom. Wir könnten zu $p$ auch sagen, wie oft das Störglied (aber ohne das oben beschriebene Polynom) als Lösung im Fundamentalsystem auftaucht.
Wie du siehst, enthält die Tabelle im Prinzip nur zwei verschiedene Fälle. Diese reichen uns jedoch vollkommen aus! Da viele Probleme damit haben, korrekte Ansatzfunktionen nach Art der Störfunktion zu bestimmen, kommen nun viele Beispiele dazu:
Beachte, dass bei der Identifikation der Struktur des Störglieds auch Zahlen gleich Null sein können, z.B. wenn $\pmb{a}$ keine Nullstelle im char. Polynom ist (was häufig der Fall ist), dann ist $\pmb{p=0}$ und somit $\pmb{x^p=1}$.
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=5 {\ =(5+0x+0x^2+\ldots)\cdot e^{0x}}\\
&\text{Nullstellen des char. Polynoms: }\lambda_1=1, \ \lambda_2=3, \ \lambda_3=4\\ \\
&\Rightarrow y_p:= (A_0) {e^{0x}\cdot x^0}
\end{align*}
\begin{align*}
&\text{DGL}: \ldots ,\quad \text{ Störglied } b(x)=3 \ =(3+0x+0x^2+\ldots)e^{0\cdot x}\\
&\text{Nullstellen des char. Polynoms}: \underbrace{\lambda_1=0}_{!}, \underbrace{\lambda_2=0}_{!}, \lambda_3=2\\ \\
&\Rightarrow y_p:= (A_0) {e^{0x}}\cdot x^2
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=x^2 \ =(0+0x+1x^2+0x^3+0x^4+\ldots) e^{0x}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=-2, \lambda_2=5\\ \\
&\Rightarrow y_p:=(A_0+A_1x+A_2x^2) e^{0x}\cdot x^0
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)= e^{2x} \ =(1+0x+0x^2+\ldots) e^{2x}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=-1, \ \lambda_2=1, \ \lambda_3=4\\ \\
&\Rightarrow y_p:=(A_0) e^{2x} {\cdot x^0}
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=(2x-x^3) e^{x} {\ =(0+2x+0x^2-1x^3+0x^4+0x^5+\ldots)e^{1x}}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=-1, \lambda_2=3\\ \\
&\Rightarrow y_p:=(A_0+A_1x+A_2x^2+A_3x^3) e^{x}{\cdot x^0}
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=x e^{2x}{\ =(0+1x+0x^2+0x^3+\ldots) e^{2x}}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=-1, \underbrace{\lambda_2=2}_{!}, \underbrace{\lambda_3=2}_{!}, \underbrace{\lambda_4=2}_{!}\\ \\
&\Rightarrow y_p:=(A_0+A_1x) e^{2x}\cdot x^3=(A_0x^3+A_1x^4) e^{2x}
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=x\sin(2x){\ =(0+1x+0x^2+0x^3+\ldots) e^{0x}\sin(2x)}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=0, \lambda_2=2\\ \\
&\Rightarrow y_p:=(A_0+A_1x)\cos(2x){\cdot x^0}+(B_0+B_1x)\sin(2x){\cdot x^0}
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)=2\cos(3x){\ =(2+0x+0x^2+\ldots) e^{0\cdot x}\cos(3x)}\\
&\text{Nullstellen des char. Polynoms}: \underbrace{\lambda_{1,2}=\pm 3i{\ =0\pm 3i}}_{!}, \lambda_3=4\\ \\
&\Rightarrow y_p:={(}A_0{)}{e^{0x}}\cos(3x)\cdot x+{(B_0)}{ e^{0x}}\sin(3x)\cdot x
\end{align*}
\begin{align*}
&\text{DGL}: … ,\quad \text{ Störglied } b(x)= e^{-2x}\cos(x){\ =(1+0x+0x^2+\ldots) e^{-2x}\cos(x)}\\
&\text{Nullstellen des char. Polynoms}: \lambda_1=-2, \lambda_2=1\\ \\
&\Rightarrow y_p:={(}A_0{)} e^{-2x}\cos(x){\cdot x^0}+(B_0) e^{-2x}\sin(x){\cdot x^0}
\end{align*}
$y_p$: VdK – Variation der Konstanten
Mit der Methode VdK überführen wir in der vorher bestimmten homogenen Lösung einer DGL die Konstante in eine noch nicht näher bestimmte Funktion. Das Ganze nutzen wir dann als neue Ansatzfunktion für unsere partikuläre Lösung.
Sagen wir, die homogene Lösung (zu $y’=a_0(x)y$) ist wie folgt gegeben:
\begin{align*}
y_h&=C\cdot e^{A_0(x)}\quad\text{mit}\quad A_0(x)=\int{a_0(x)}dx\quad\text{und}\quad C\in\mathbb{R}
\end{align*}
dann:
- Variation der Konstanten von $C$ zu $C(x)$
- $\displaystyle y_p:=C(x)\cdot e^{A_0(x)}$ fungiert als Ansatzfunktion
- $y’_p$ bestimmen (beachte, dass $C(x)$ auch abgeleitet werden muss – Produktregel!)
- $y_p$ und $y’_p$ in die ursprüngliche DGL einsetzen
- Auf $C'(x)$ umformen
- $C(x)$ durch integrieren bestimmen (die „$+$ Konstante“ am Ende des Integrals ist nicht nötig!)
- $C(x)$ in $y_p$ einsetzen
$y_p$: VdK (LGS Variante)
Durch die Ausweitung der VdK auf DGLs höherer Ordnung können wir das Verfahren nach folgendem Schema abarbeiten:
Sagen wir, die homogene Lösung ist wie folgt gegeben:
\begin{align*}
y_h=C_1\cdot y_1+C_2\cdot y_2+\ldots
\end{align*}
mit $y_1$, $y_2$, $\ldots$ als Basislösungen aus dem Fundamentalsystem
- Homogene Lösung sollte mit dem Euler-Ansatz bestimmt worden sein (FS muss vorliegen)
- Variation der Konstanten:\begin{align}
&y_p=C_1(x)\cdot y_1+C_2(x)\cdot y_2+\ldots
\end{align} - Durch einen allgemeinen Ansatz kann gezeigt werden, dass die variierten Konstanten durch folgendes Gleichungssystem bestimmt werden können:
\begin{align}
\left( \begin{array}( y_1 & y_2 & \cdots & y_n \\ y’_1 &y’_2 & \cdots & y’_n \\ \vdots & \vdots & \ddots & \vdots\\ y^{(n-1)}_1 & y^{(n-1)}_2 & \cdots & y^{(n-1)}_n
\end{array}\right)
\cdot
\left( \begin{array}
CC’_1(x) \\
C’_2(x) \\
\vdots \\
C’_n(x)
\end{array}
\right) =
\left( \begin{array} 0 \\
0 \\
\vdots \\
b(x)
\end{array}\right)
\end{align} - Gleichungssystem lösen (Gauß-Algorithmus)
- $C’_1(x)$, $C’_2(x)$, … integrieren (beim Integrieren ist die „+ Konstante“ am Ende des unbestimmten Integrals nicht nötig)
- $y_p$ entsteht, wenn $C_1(x)$, $C_2(x)$, … in eingesetzt wird
$y_p$: Lösungsformel (part)
Wenn wir unsere DGL richtig typisiert haben, können wir eine inhomogene lineare DGL erster Ordnung in expliziter Form schreiben:
\begin{align}
y’&=a_0(x)y+b(x)
\end{align}
Verfahren
- DGL korrekt typisieren.
- DGL in Form $y’=a_0(x)y+b(x)$ bringen
- Lösung ist gegeben durch:
\begin{align}
y_p&= e^{A_0(x)}\cdot\int{b(x)\cdot e^{-A_0(x)}}dx\quad\text{mit}\quad A_0(x)=\int{a_0(x)}dx\quad\text{und}\quad C\in\mathbb{R}
\end{align}Denn der allgemeine Ablauf der VdK läuft bei inhomogenen linearen DGLs erster Ordnung immer auf diese Lösungsform hinaus!
Bei beiden Integralen in ist die „+ Konstante“ am Ende des unbestimmten Integrals nicht nötig!
Beispiele: Lineare Differentialgleichungen erster Ordnung
Beispiel 1
Finde alle Funktionen $y$ für die $y’=4y+2 e^{4x}+\cos(2x)$ gilt.
Dies ist eine inhomogene lineare DGL 1. Ordnung mit Konstanten vor den Funktionen. Für die partikuläre Lösung nutzen wir die Superposition der Einzellösungen für die Inhomogenitäten $2 e^{4x}$ und $\cos(2x)$
Löse zugehörige homogene DGL $y’=4y$
\begin{alignat*}{2}
\text{Euler-Ansatz:}\quad&& y’=4y \Rightarrow \lambda=4\\
\Rightarrow&& \text{FS: }={ e^{4x}}\\
\Rightarrow&& y_h=C e^{4x}
\end{alignat*}
Partikuläre Lösung der inhomogenen DGL $y’=4y+2 e^{4x}$
Störgliedansatz: $y_{p,1}:=A_0 e^{4x}\cdot x=A_0x e^{4x}$
Ableitung: $y’_{p,1}=A_0\left( e^{4x}+x e^{4x}\cdot 4\right)=A_0(1+4x) e^{4x}$
In DGL einsetzen:
\begin{alignat*}{2}
&&A_0(1+4x) e^{4x}&=4\cdot A_0x e^{4x}+2 e^{4x}\\
\Rightarrow&&A_0+4A_0x&=4A_0x+2\\
\Rightarrow&&A_0&=2\\
\Rightarrow&&y_{p,1}&=2x e^{4x}
\end{alignat*}
Partikuläre Lösung der inhomogenen DGL $y’=4y+\cos(2x)$
Störgliedansatz: $y_{p,2}:=A_0\cos(2x)+B_0\sin(2x)$
Ableitung: $y’_{p,2}=-2A_0\sin(2x)+2B_0\cos(2x)$
In DGL einsetzen:
\begin{alignat*}{2}
&&-2A_0\sin(2x)+2B_0\cos(2x)&=4\cdot(A_0\cos(2x)+B_0\sin(2x))+\cos(2x)\\
\Rightarrow&&\sin(2x)(-2A_0-4B_0)+\cos(2x)(-4A_0+2B_0)&={0\cdot\sin(2x)+1\cdot}\cos(2x)
\end{alignat*}
Koeffizientenvergleich: $-2A_0-4B_0=0$ und $-4A_0+2B_0=1$ (ist ein LGS!)
LGS lösen mit Gauß-Algorithmus ergibt: $A_0=-\frac{1}{5}$ und $B_0=\frac{1}{10}$
Also ist $y_{p,2}=-\frac{1}{5}\cos(2x)+\frac{1}{10}\sin(2x)$
$\Rightarrow y=y_h+y_{p,1}+y_{p,2}=C e^{4x}+2x e^{4x}-\frac{1}{5}\cos(2x)+\frac{1}{10}\sin(2x)$
Beispiel 2
Finde alle Funktionen $y$ für die $(1+x^4)^2y’+4x^3(1+x^4)y+x=0$ gilt.
Dies ist eine inhomogene lineare DGL 1. Ordnung mit Variablen vor den Funktionen.
Homogene Lösung durch: TdV oder Lösungsformel (hom).
\begin{alignat*}{2}
\text{TdV:}\quad&&(1+x^4)^2y’+4x^3(1+x^4)y&=0\Rightarrow y’=-\frac{4x^3}{1+x^4}y\Rightarrow \frac{dy}{dx}=-\frac{4x^3}{1+x^4}y\\
\Rightarrow&& \frac{1}{y}dy&=-\frac{4x^3}{1+x^4}dx\\
\Rightarrow&& \int\frac{1}{y}dy&=\int-\frac{4x^3}{1+x^4}dx\\
\stackrel{\ast^1}{\Rightarrow}&& \ln |{y}|&=-\ln(1+x^4)+C_1\\
\Rightarrow&& |{y}|&= e^{-\ln(1+x^4)+C_1}=\frac{ e^{C_1}}{ e^{\ln(1+x^4)}}\\
\Rightarrow&& y_h&=C\frac{1}{1+x^4}
\end{alignat*}
\begin{alignat*}{2}
\text{oder Lösungsformel:}\quad&&y’&=-\frac{4x^3}{1+x^4}y\\
\Rightarrow&& y_h&=C e^{A_0(x)}\quad\text{mit}\quad A_0(x)=\int-\frac{4x^3}{1+x^4}dx\stackrel{\ast^1}{=}-\ln(1+x^4)\\
\Rightarrow&& y_h&=C e^{-\ln(1+x^4)}=C\frac{1}{1+x^4}
\end{alignat*}
$*^1$: Integrale lösen durch Substitution auf $x$-Seite: $z:=1+x^4$
Partikuläre Lösung durch: VdK oder Lösungsformel (part).
\begin{alignat*}{2}
\text{VdK:}\quad&&y_p&:=C(x)\frac{1}{1+x^4}\\
\Rightarrow&&y’_p&:=C'(x)\frac{1}{1+x^4}+C(x)\left(-\frac{4x^3}{(1+x^4)^2}\right)
\end{alignat*}
\begin{alignat*}{2}
\stackrel{\text{in DGL}}{\Rightarrow}&&(1+x^4)^2\biggl(C'(x)\frac{1}{1+x^4}+C(x)\left(-\frac{4x^3}{(1+x^4)^2}\right)\biggr)+4x^3(1+x^4)C(x)\frac{1}{1+x^4}+x&=0\\
\Rightarrow&&(1+x^4)C'(x)\frac{1}{1}+C(x)\left(-\frac{4x^3}{1}\right)+4x^3C(x)\frac{1}{1}+x&=0
\end{alignat*}
\begin{alignat*}{2}
\Rightarrow&&(1+x^4)C'(x)+x&=0\\
\Rightarrow&&C'(x)&=-\frac{x}{1+x^4}\\
\Rightarrow&&C(x)&=\int-\frac{x}{1+x^4}dx\\
\Rightarrow&&C(x)&=-\frac{1}{2}\arctan(x^2)\\
\Rightarrow&&y_p&=-\frac{1}{2}\arctan(x^2)\frac{1}{1+x^4}\\
\end{alignat*}
Also:
\begin{align*}
y_{allg}=y_h+y_p=C\frac{1}{1+x^4}-\frac{1}{2}\arctan(x^2)\frac{1}{1+x^4}
\end{align*}
Beispiele: Lineare DGL höherer Ordnung mit konstanten Koeffizienten
AWP:$\quad y“’+4y“+y‘-6y=0, \quad y(0)=y'(0)=0, y“(0)=1$
\begin{alignat*}{2}
&& y“’+4y“+y‘-6y&=0\\
\Leftrightarrow&& \lambda^3+4\lambda^2+\lambda-6&=0
\end{alignat*}
Nullstelle $\lambda=1$ erraten und Polynom durch Horner-Schema (oder Pol.div.) aufgetrennt:
\begin{alignat*}{2}
&& (\lambda-1)(\lambda^2+5\lambda+6)&=0\\
\stackrel{\text{pq-Formel}}{\Rightarrow}&& \underbrace{(\lambda-1)}_{\lambda=1}\underbrace{(\lambda+2)}_{\lambda=-2}\underbrace{(\lambda+3)}_{\lambda=-3}&=0
\end{alignat*}
Fundamentalsystem:
\begin{align*}
\text{FS}=\left\{e^{1x},e^{-2x},e^{-3x}\right\}
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=C_1 e^{1x}+C_2 e^{-2x}+C_3 e^{-3x}
\end{align*}
AWP lösen: Ableitungen:
\begin{align*}
y’&=C_1 e^{1x}-2C_2 e^{-2x}-3C_3 e^{-3x}\\
y“&=C_1 e^{1x}+4C_2 e^{-2x}+9C_3 e^{-3x}
\end{align*}
Anfangswerte einsetzen und das entstehende LGS lösen:
\begin{align*}
y(0)&=C_1 e^{1\cdot 0}+C_2 e^{-2\cdot 0}+C_3 e^{-3\cdot 0}=C_1+C_2+C_3=0\\
y'(0)&=C_1 e^{1\cdot 0}-2C_2 e^{-2\cdot 0}-3C_3 e^{-3\cdot 0}=C_1-2C_2-3C_3=0\\
y“(0)&=C_1 e^{1\cdot 0}+4C_2 e^{-2\cdot 0\cdot 0}+9C_3 e^{-3\cdot 0}=C_1+4C_2+9C_3=1\\[4mm]
&\left\{\begin{array}{rrrrrcl}
C_1&+&C_2& +& C_3& = & 0 \\
C_1&-&2C_2& -& 3C_3& = & 0 \\
C_1&+&4C_2& +& 9C_3& = & 1
\end{array}\right.\quad\stackrel{\text{Gauß-Alg.}}{\rightarrow}\quad C_1=\frac{1}{12},\ C_2=-\frac{1}{3},\ C_3=\frac{1}{4}
\end{align*}
\begin{align*}
\Rightarrow y_{spez}=\frac{1}{12} e^{1x}-\frac{1}{3} e^{-2x}+\frac{1}{4} e^{-3x}\quad\text{löst das AWP.}
\end{align*}
Weiteres Beispiel
Finde alle Funktionen $y$, für die $\quad y“’+3y“+3y’+y=0 \quad$ gilt.
\begin{alignat*}{2}
&& y“’+3y“+3y’+y&=0\\
{\Rightarrow}&& \lambda^3+3\lambda^2+3\lambda+1&=0
\end{alignat*}
Nullstelle $\lambda=-1$ erraten und Polynom durch Horner-Schema (oder Pol.div.) aufgetrennt:
\begin{alignat*}{2}
&& (\lambda+1)(\lambda^2+2\lambda+1)&=0\\
\stackrel{\text{pq-Formel}}{\Rightarrow}&& \underbrace{(\lambda+1)}_{\lambda=-1}\underbrace{(\lambda+1)}_{\lambda=-1}\underbrace{(\lambda+1)}_{\lambda=-1}&=0
\end{alignat*}
Fundamentalsystem:
\begin{align*}
\text{FS}=\left\{e^{-1x},x e^{-1x},x^2 e^{-1x}\right\}
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=C_1 e^{-x}+C_2x e^{-x}+C_3x^2 e^{-x}
\end{align*}
Finde alle Funktionen $y$, für die $\quad y^{(4)}-6y“’+22y“-30y’+13y=0 \quad$ gilt.
\begin{alignat*}{2}
&& y^{(4)}-6y“’+22y“-30y’+13y&=0\\
{\Rightarrow}&& \lambda^4-6\lambda^3+22\lambda^2-30\lambda+13&=0
\end{alignat*}
Nullstelle $\lambda=1$ erraten und Polynom durch Horner-Schema (oder Pol.div.) aufgetrennt:
\begin{align*}
\underbrace{(\lambda-1)}_{\lambda=1}\underbrace{(\lambda^3-5\lambda^2+17\lambda-13)}_{\lambda=?}=0
\end{align*}
Nullstelle $\lambda=1$ des Restpolynoms erraten (also doppelte Nullstelle) und Restpolynom durch Horner-Schema (oder Pol.div.) nochmals aufgetrennt:
\begin{align*}
\underbrace{(\lambda-1)^2}_{\lambda=1}\underbrace{(\lambda^2-4\lambda+13)}_{\lambda=?}=0
\end{align*}
Durch pq-Formel die komplex konjugierte Nullstelle $\lambda=2\pm 3i$ bestimmt.
Fundamentalsystem:
\begin{align*}
\text{FS}=\left\{e^{1x},x e^{1x}, e^{2x}\cos(3x), e^{2x}\sin(3x)\right\}
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=C_1 e^{x}+C_2x e^{x}+C_3 e^{2x}\cos(3x)+C_4 e^{2x}\sin(3x)
\end{align*}
Weiteres Beispiel
Finde alle Funktionen $y$, für die$\quad 2y“+8y’=2 e^{-4x}\quad$ gilt.
\begin{alignat*}{2}
&& 2y“+8y’&=2 e^{-4x}\\
\Rightarrow&&y“+4y’&= e^{-4x}\quad\text{(da vor höchster Ableitung 1 als Faktor stehen muss.)}
\end{alignat*}
Homogene Lösung
Fundamentalsystem:
\begin{align*}
\text{FS}=\left\{e^{0x},e^{-4x}\right\}=\left\{1,e^{-4x}\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_h=C_1\cdot 1+C_2 \cdot e^{-4x}=C_1+C_2 e^{-4x}
\end{align*}
Partikuläre Lösung bestimmen: Störgliedansatz:
\begin{align*}
y_p:={(A_0)}\cdot e^{-4x}\cdot x^{1}=A_0x e^{-4x}
\end{align*}
Ableitungen bestimmen:
\begin{align*}
y_p’&=A_0\Bigl(1 e^{-4x}+x e^{-4x}\cdot(-4)\Bigr)=A_0(1-4x) e^{-4x}\\
y_p“&=A_0\Bigr((-4) e^{-4x}+(1-4x) e^{-4x}\cdot(-4)\Bigl)=A_0(-8+16x) e^{-4x}
\end{align*}
In DGL einsetzen:
\begin{alignat*}{2}
&&y“+4y’&= e^{-4x}\\
\Rightarrow&&A_0(-8+16x) e^{-4x}+4\cdot A_0(1-4x) e^{-4x}&= e^{-4x}\\
\Rightarrow&& -8A_0+16xA_0+4A_0-16xA_0&=1\\
\Rightarrow&& -4A_0&=1\\
\Rightarrow&& A_0&=-\frac{1}{4}
\end{alignat*}
Also gilt:
\begin{align*}
y_p=-\frac{1}{4}x e^{-4x}
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=y_h+y_p=C_1+C_2 e^{-4x}-\frac{1}{4}x e^{-4x}
\end{align*}
Partikuläre Lösung bestimmen: VdK (LGS-Variante):
\begin{align*}
y_p=C_1(x)+C_2(x) e^{-4x}
\end{align*}
Löse das Gleichungssystem:
\begin{align*}
\left(
\begin{array}{cc}
1 & e^{-4x} \\
0 & -4 e^{-4x}
\end{array}
\right)
\cdot
\left(
\begin{array}
CC’_1(x) \\
C’_2(x)
\end{array}
\right)
=
\left(
\begin{array}
00 \\
e^{-4x}
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{cc|c}
11 & e^{-4x} & 0 \\
0 & -4 e^{-4x} & e^{-4x}
\end{array} \right) \\
\Rightarrow
\left( C’_2(x)=\frac{ e^{-4x}}{-4 e^{-4x}}=-\frac{1}{4}\quad C’_1(x)-\frac{1}{4} e^{-4x}=0 \quad C’_1(x)=\frac{1}{4} e^{-4x} \right)
\end{align*}
Integrieren:
\begin{align*}
C_1(x)&=\frac{1}{4}\cdot\left(-\frac{1}{4}\right) e^{-4x}=-\frac{1}{16} e^{-4x}\quad\text{und}\quad C_2(x)=-\frac{1}{4}x
\end{align*}
Partikuläre Lösung:
\begin{align*}
y_p=-\frac{1}{16} e^{-4x}-\frac{1}{4}x e^{-4x}
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=y_h+y_p=C_1+C_2 e^{-4x}-\frac{1}{16} e^{-4x}-\frac{1}{4}x e^{-4x}
\end{align*}
Den Term $C_2 e^{-4x}-\frac{1}{16} e^{-4x}$ könnten wir zusammenfassen zu $(C_2-\frac{1}{16}) e^{-4x}$, wobei $C_2-\frac{1}{16}$ wieder eine Konstante aus $\mathbb{R}$ ist. Damit würden wir bei exakt der Lösung landen, die wir durch den Störgliedansatz bestimmt haben.
Weiteres Beispiel
$\text{RWP:} \quad y“-2y’+y=\frac{ e^{x}}{x^2},\quad y(1)=y'(1)= e$Homogene Lösung (also löse $y“-2y’+y=0$)
Fundamentalsystem:
\begin{align*}
\text{FS}=\left\{e^{1x},x e^{1x}\right\}
\end{align*}
Homogene Lösung:
\begin{align*}
y_h=C_1 e^x+C_2x e^x
\end{align*}
Partikuläre Lösung bestimmen: Störgliedansatz:
Da $\frac{ e^{x}}{x^2}$ keiner Struktur aus der Ansatztabelle entspricht, können wir die partikuläre Lösung so nicht ohne Weiteres bestimmen.
Partikuläre Lösung bestimmen: VdK (LGS-Variante):
\begin{align*}
y_p=C_1(x) e^x+C_2(x)x e^x
\end{align*}
Löse das Gleichungssystem:
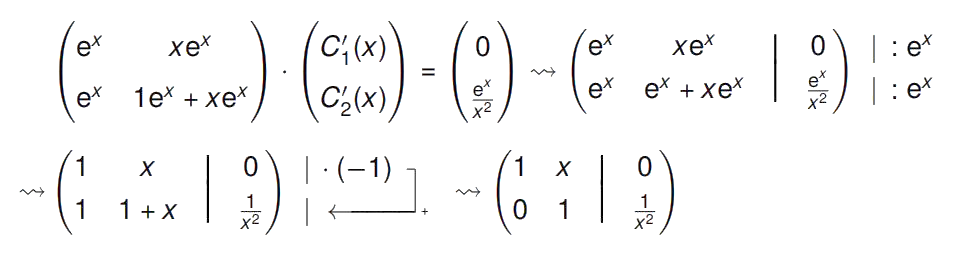
\begin{align*}
C’_2=\frac{1}{x^2}\quad C’_1+\frac{1}{x^2}\cdot x=0\quad C’_1=-\frac{1}{x}
\end{align*}
Integrieren:
\begin{align*}
C_1(x)&=-\ln |{x}|\quad\text{und}\quad C_2(x)=\int{\frac{1}{x^2}}dx=\int{x^{-2}}dx=\frac{1}{-1}x^{-1}=-\frac{1}{x}
\end{align*}
Partikuläre Lösung:
\begin{align*}
y_p=-\ln|{x}| e^x-\frac{1}{x}x e^x=-\ln |{x}| e^x- e^x
\end{align*}
Allgemeine Lösung:
\begin{align*}
y_{allg}=y_h+y_p=C_1 e^x+C_2x e^x-\ln |{x}| e^x- e^x
\end{align*}
RWP lösen: Ableitungen:
\begin{align*}
y’&=C_1 e^x+C_2 e^x+C_2x e^x-\frac{e^x}{x}-\ln |{x}| e^x- e^x
\end{align*}
Randwerte einsetzen und das entstehende LGS lösen:
\begin{align*}
y(1)&=C_1 e^1+C_2\cdot 1\cdot e^1-\ln |{1}| e^1- e^1=C_1 e+C_2 e-e= e\\
y'(1)&=C_1 e^1+C_2 e^1+C_2\cdot 1\cdot e^1-\frac{e^1}{1}-\ln |{1}| e^1-e^1=C_1 e+C_22 e-2 e=e\\[4mm]
&
\left\{
\begin{array}{rrrrrcl}
C_1 e&+&C_2 e& = & 2 e \\
C_1 e&+&2C_2 e & = & 3 e
\end{array}\right.\quad\stackrel{\text{Gaus-Alg.}}{\Rightarrow}\quad C_1=1,\ C_2=1
\end{align*}
\begin{align*}
\quad y_{spez}=e^x+x e^x-\ln |{x}| e^x-e^x=e^x\left(x-\ln |x| \right)\quad\text{löst das RWP.}
\end{align*}
Beispiele: Nicht-lineare DGL erster Ordnung
Beispiel 1
Löse das AWP: $y’y^3= e^x,\quad y(0)=3$
Lösen per TdV:
\begin{align*}{2}
&&\frac{dy}{dx}y^3&= e^x\quad y^3 dy= e^x dx\\
\Leftrightarrow&& \int_3^y y^3 dy&=\int_0^x e^x dx\\
\Leftrightarrow&& \frac{1}{4}y^4-\frac{1}{4}3^4&= e^x – e^0\ \Bigl|\Bigr.\ \cdot 4\\
\Leftrightarrow&& y^4-81&=4 e^x-4\\
\Leftrightarrow&& y^4&=4 e^x+77\\
\Leftrightarrow&& y=y_{spez}&=\sqrt[4]{4 e^x+77}\text{ (pos. Lsg., da AWP} y(0)=3>0)
\end{align*}
Löse das AWP: $\frac{y‘}{\sin^3(x)}=y\cos(x)\ln(y),\quad y\left(\frac{\pi}{4}\right)=e$
Lösen per TdV:
\begin{align*}
&&\frac{dy}{dx}\cdot\frac{1}{\sin^3(x)}&=y\cos(x)\ln(y)\Leftrightarrow \frac{1}{y\ln(y)}dy=\cos(x)\sin^3(x) dx\\
\Leftrightarrow&& \int_e^y \frac{1}{y\ln(y)}dy&=\int_{\frac{\pi}{4}}^x \cos(x)\sin^3(x) dx\\
\stackrel{\ast^1}{\Leftrightarrow}
&&\ln\bigl(\ln(y)\bigr)-\ln\bigl(\ln(e)\bigr)&=\frac{1}{4}\sin^4(x)-\frac{1}{4}\sin^4\left(\frac{\pi}{4}\right)\\
\Leftrightarrow&& \ln\bigl(\ln(y)\bigr)-\ln\bigl(1\bigr)&=\frac{1}{4}\sin^4(x)-\frac{1}{4}\left(\frac{1}{\sqrt{2}}\right)^4\\
\Leftrightarrow&& \ln\bigl(\ln(y)\bigr)-0&=\frac{1}{4}\sin^4(x)-\frac{1}{4}\cdot \frac{1}{4}\\
\Leftrightarrow&& \ln\bigl(\ln(y)\bigr)&=\frac{1}{4}\sin^4(x)-\frac{1}{16}\\
\Leftrightarrow&& \ln(y)&=e^{\frac{1}{4}\sin^4(x)-\frac{1}{16}}\\
\Leftrightarrow&& y=y_{spez}&=e^{\left(e^{\frac{1}{4}\sin^4(x)-\frac{1}{16}}\right)}=\text{e}\left\{e^{\frac{1}{4}\sin^4(x)-\frac{1}{16}}\right\}
\end{align*}
$\ast^1: \text{Integrale lösen durch Substitution auf} \ y$-Seite: $z:=\ln(y)$ und Substitution auf $x$-Seite: $z:=\sin(x)$
Beispiel 2
Löse das AWP: $2y’y=2x\cdot\frac{1+y^4}{1+x^2},\quad y(0)=1$
Lösen per TdV:
\begin{align*}{2}
&&\frac{dy}{dx}2y&=2x\cdot\frac{1+y^4}{1+x^2}\Rightarrow \frac{2y}{1+y^4}dy=\frac{2x}{1+x^2}dx\\
\Rightarrow&& \int_1^y \frac{2y}{1+y^4} dy&=\int_0^x \frac{2x}{1+x^2} dx\\
\stackrel{\ast^1}{\Rightarrow}&& \arctan(y^2)-\arctan(1^2)&=\ln(1+x^2)-\ln(1+0)\\
\Rightarrow&& \arctan(y^2)-\frac{\pi}{4}&=\ln(1+x^2)\\
\Rightarrow&& \arctan(y^2)&=\ln(1+x^2)+\frac{\pi}{4}\\
\Rightarrow&& y^2&=\tan\left(\ln(1+x^2)+\frac{\pi}{4}\right)\\
\Rightarrow&& y=y_{spez}&=\sqrt{\tan\left(\ln(1+x^2)+\frac{\pi}{4}\right)}\text{ (pos. Lsg., da AWP y(0)=1>0)}
\end{align*}
$\ast^1$: Integrale lösen durch Substitution auf $y$-Seite: $z:=y^2$ und Substitution auf $x$-Seite: $z:=1+x^2$
Nicht-lineare DGLs können auch gewisse Strukturen aufweisen, für die es spezielle Lösungsansätze durch Substitutionen gibt. In den nachfolgenden Unterkapiteln stellen wir zwei dieser speziellen Strukturen vor.
Bernoulli-Differentialgleichung
Wenn sich eine DGL in der Form
\begin{align}
y’=p(x)y+q(x)y^a\text{ mit } a\in\mathbb{R}\setminus\{0,1\}
\end{align}
schreiben lässt, dann ist diese als Bernoulli-DGL typisiert (gewöhnlich, 1. Ordnung, nicht-linear wegen $y^a$).
Für $a=0$ wäre $y’=p(x)y+q(x)y^0\Rightarrow y’=p(x)y+q(x)$ eine inhomogene lineare DGL 1. Ordnung.
Für $a=1$ wäre $y’=p(x)y+q(x)y^1\Rightarrow y’=\Bigl(p(x)+q(x)\Bigr)y$ eine homogene lineare DGL 1. Ordnung.
Diese lässt sich mit dem Ansatz einer Substitution $z$ lösen:
\begin{align}
z:=y^{1-a}
\end{align}
Damit können wir die DGL auf eine inhomogene lineare DGL 1. Ordnung zurückführen, welche dann leicht zu lösen ist.
Herleitung der substituierten DGL:
\begin{align*}
\Rightarrow y&=\sqrt[1-a]{z}=z^{\frac{1}{1-a}}\\
\Rightarrow y’&=\frac{1}{1-a}\cdot z^{\frac{1}{1-a}-1}\cdot z’=\frac{1}{1-n}\cdot z^{\frac{a}{1-a}}\cdot z‘
\end{align*}
In $y’=p(x)y+q(x)y^a$ einsetzen:
\begin{align*}{3}
&&\frac{1}{1-a}\cdot z^{\frac{a}{1-a}}\cdot z’&=p(x)\cdot z^{\frac{1}{1-a}}+q(x)\cdot\left(z^{\frac{1}{1-a}}\right)^a&&\ \bigl|\bigr.\ \cdot(1-a)\\
\Rightarrow&&z^{\frac{a}{1-a}}\cdot z’&=(1-a)p(x)\cdot z^{\frac{1}{1-a}}+(1-a)q(x)\cdot z^{\frac{a}{1-a}}&&\ \bigl|\bigr.\ :z^{\frac{a}{1-a}}\\
\Rightarrow&&z’&=(1-a)p(x)\cdot z^{\frac{1}{1-a}-\frac{a}{1-a}}+(1-a)q(x)\cdot z^{\frac{a}{1-a}-\frac{a}{1-a}}&&\\
\Rightarrow&&z’&=(1-a)p(x)\cdot z^{1}+(1-a)q(x)\cdot z^{0}&&\\
\Rightarrow&&z’&=(1-a)p(x)\cdot z+(1-a)q(x)&&
\end{align*}
Im Anschluss wird rücksubstituiert und auf $y$ aufgelöst.
Lösungsansatz Bernoulli-DGL
- DGL korrekt typisieren
- DGL in Form $y’=p(x)y+q(x)y^a$ schreiben
- Substituieren: $z:=y^{1-a}$ setzen
- Ausgangs-DGL wird zur substituierten DGL $z’=(1-a)p(x)\cdot z+(1-a)q(x)$
- Substituierte DGL ist eine inhomogene lineare DGL 1. Ordnung
- Substituierte DGL mit Übergeordneten Lösungsverfahren lösen.
- Rücksubstitution von $z$ nach $y^{1-a}$
- Nach $y$ auflösen
Beispiel
Löse das AWP $y’+y-y^3=0,\quad y(0)=2$.
Die DGL ist eine Bernoulli-DGL.
\begin{align*}{2}
&&y’+y-y^3&=0\\
\Rightarrow&&y’&=-y+y^3\\
\Rightarrow&&y’=&p(x)y+q(x)y^a\Rightarrow p(x)=-1,\ q(x)=1,\ a=3,\ z:=y^{1-3}=y^{-2}\\
\stackrel{\text{subst.}}{\Rightarrow}&& z’&=(1-3)(-1)z+(1-3)(1)\\
\Rightarrow&& z’&=2z-2
\end{align*}
Inhomogene DGL $z’=2z-2$ per TdV lösen, da separierbar:
\begin{align*}{2}
&&z’&=2z-2\Rightarrow \frac{dz}{dx}=(2)(z-1)\Rightarrow\frac{1}{z-1}dz=2 dx\\
\Rightarrow&&\int\frac{1}{z-1}dz&=\int 2 dx\\
\Rightarrow&& \ln(z-1)&=2x+C_1\\
\Rightarrow&& z-1&=e^{2x+C_1}=C e^{2x}\\
\Rightarrow&& z=z_{allg}&=C e^{2x}+1
\end{align*}
Rücksubstitution: $z=y^{-2}=\frac{1}{y^2}$
\begin{align*}{2}
\Rightarrow&& \frac{1}{y^2}&=C e^{2x}+1 \\
\Rightarrow&& y=y_{allg}&=\pm\sqrt{\frac{1}{C e^{2x}+1}},\ C\in\mathbb{R}\
\end{align*}
AWP lösen und die spezielle Lösung der DGL bestimmen:
\begin{align*}{2}
&&y(0)&\stackrel{1}{=}\sqrt{\frac{1}{C e^{2\cdot 0}+1}}\stackrel{!}{=}2\\
\Rightarrow&&\sqrt{\frac{1}{C+1}}&=2\Rightarrow\frac{1}{C+1}=4\Rightarrow 1=4C+4\Rightarrow C=-\frac{3}{4}\\
\Rightarrow &&y=y_{spez}&=\sqrt{\frac{1}{-\frac{3}{4} e^{2x}+1}}
\end{align*}
$\ast^1$: Die negative Lösung aus $y_{allg}$ entfällt aufgrund des positiven $y_0$.
\begin{align*}
%y’+2xy&=y^2 e^{x^2} \\[1mm]
%3y’+y&=\frac{1}{y^2} \\[1mm]
%xy’+2y&=-x^3\cos(x)y^2}
\end{align*}
Eulerhomogene-DGL
Wenn sich eine nicht-lineare DGL erster Ordnung in der Form
\begin{align*}
y’=f\left(\frac{y}{x}\right)
\end{align*}
schreiben lässt, dann nennt sich diese DGL Eulerhomogene-DGL. Mit $f\left(\frac{y}{x}\right)$ ist gemeint, dass dort der Term $\frac{y}{x}$ in jeglicher Funktion verschachtelt eingebunden sein kann z.B. $y’=\frac{y}{x}-1-e^{\frac{y}{x}}$.
Die Bezeichnung „Eulerhomogene-DGL“ lässt vermuten, dass es sich um eine homo\-gene DGL im Sinne der Typisierung von DGLs handelt. Das ist jedoch nicht der Fall!
Solch eine DGL lässt sich ebenfalls mit dem Ansatz einer Substitution $z$ lösen:
\begin{align}{2}
&&z&:=\frac{y}{x}\notag\\
\Rightarrow &&y&=z\cdot x\\
\Rightarrow &&y’&=z’\cdot x+z\cdot 1
\end{align}
Beachte, dass $z$ eine Fkt. von $x$ ist (also Produktregel beim Ableiten!).
Lösungsansatz Eulerhomogene-DGL
- DGL korrekt typisieren
- DGL lässt sich schreiben als $y’=f(\frac{y}{x})$
- Substitutionen $\Rightarrow y=z\cdot x$ und $\Rightarrow y’=z’\cdot x+z\cdot 1$ nutzen und in die Ausgangs-DGL einsetzen.
- Nun versuchen, die substituierte DGL per TdV zu lösen
- Rücksubstitution von $z$ nach $\frac{y}{x}$
- Auf $y$ auflösen
Beispiel
Löse das AWP $y’=1+2\cdot\frac{y}{x},\quad y(1)=-3$
Substitutionen $\Rightarrow y=z\cdot x$ und $\Rightarrow y’=z’\cdot x+z\cdot 1$ nutzen:
\begin{align*}{2}
&& z’x+z&=1+2z\\
\Rightarrow&& z’x&=1+z
\end{align*}
TdV der inhomogenen DGL, da diese separierbar ist:
\begin{align*}{2}
&& \frac{dz}{dx}x&=1+z\Rightarrow\frac{dz}{1+z}=\frac{dx}{x}\\
\Rightarrow&& \int{\frac{1}{1+z}}dz&=\int{\frac{1}{x}}dx \\
\Rightarrow&& \ln|1+z|&=\ln|x|+C_1\\
\Rightarrow&& 1+z&=e^{\ln|x|+C_1}\\
\Rightarrow&& 1+z&=Cx\\
\Rightarrow&& z&=Cx-1
\end{align*}
Rücksubstitution:
\begin{align*}{2}
&& \frac{y}{x}&=Cx-1 \\
\Rightarrow&& y_{allg}&=Cx^2-x,\ C\in\mathbb{R}\
\end{align*}
AWP lösen:
\begin{align*}{2}
&&y(1)&=C\cdot 1^2-1=C-1\stackrel{!}{=}-3\\
\Rightarrow&&C&=-2\\
\Rightarrow&&y_{spez}&=-2x^2-x
\end{align*}
Wir hätten hier auch die üblichen Methoden für eine inhomogene lineare DGL 1. Ordnung sofort anwenden können.
Weiteres Beispiel
Finde alle Funktionen, für die $xy’=y-x-x e^{\frac{y}{x}}$ gilt.
\begin{align*}
xy’=y-x-x\exp^{\frac{y}{x}}\Rightarrow y’=\frac{y}{x}-1- e^{\frac{y}{x}}
\end{align*}
Substitutionen $\Rightarrow y=z\cdot x$ und $\Rightarrow y’=z’\cdot x+z\cdot 1$ nutzen:
\begin{align*}{2}
&& z’x+z&=z-1-\exp^z\\
\Rightarrow&& z’x&=-1-\exp^z
\end{align*}
TdV der nicht-linearen DGL:
\begin{align*}{2}
&& \frac{dz}{dx}x&=-1-e^z\Rightarrow\frac{1}{-1-e^z}dz=\frac{1}{x}dx \\
\Rightarrow&& -\int{\frac{1}{1+ e^z}}dz&=\int{\frac{1}{x}}dx\\
\stackrel{\ast^1}{\Rightarrow}&& -\left(-\ln|{1+e^z}|+\ln|{e^z}|\right)&=\ln|{x}|+C_1\\
\stackrel{\ast^2}{\Rightarrow}&& \ln|{1+e^z}|-\ln|{e^z}|&=\ln|{x}|+C_1\\
\Rightarrow&& \ln|{\frac{1+e^z}{e^z}}|&=\ln|{x}|+C_1\\
\Rightarrow&& \frac{1+e^z}{e^z}&=e^{\ln|{x}|+C_1}\\
\Rightarrow&& \frac{1+e^z}{e^z}&=e^{C_1}\cdot e^{\ln|{x}|}\\
\Rightarrow&& \frac{1}{e^z}+\frac{e^z}{e^z}&=Cx\\
\Rightarrow&& \frac{1}{e^z}+1&=Cx\\
\Rightarrow&& \frac{1}{e^z}&=Cx-1\\
\Rightarrow&& e^z&=\frac{1}{Cx-1}\\
\Rightarrow&& z&=\ln\left(\frac{1}{Cx-1}\right)\\
\Rightarrow&& z&=\ln(1)-\ln(Cx-1)\\
\Rightarrow&& z&=-\ln(Cx-1)
\end{align*}
$\ast^1$: Das Integral lösen durch Substitution $z=:\ln(u)\ \Leftrightarrow\ dz=\frac{1}{u}du$, und dann PBZ.\\
$\ast^2$: Den Term $\ln|{e^z}|$ könnten wir auch zu $z$ vereinfachen und danach die e-Funktion mit Potenzgesetzen nutzen.
Rücksubstitution:
\begin{align*}{2}
&& \frac{y}{x}&=-\ln(Cx-1) \\
\Rightarrow&& y_{allg}&=-x\ln(Cx-1),\ C\in\mathbb{R}\
\end{align*}