
Lineare Unabhängigkeit
Eine Familie von Vektoren ist linear unabhängig, wenn keine Linearkombination der Vektoren den Nullvektor ergibt, außer alle Vektoren werden mit Null multiplizieren. In anderen Worten ausgedrückt ist das gleichbedeutend mit: Eine Familie von Vektoren ist linear unabhängig, wenn sich kein einziger Vektor aus der Familie durch eine Linearkombination der verbleibenden Vektoren aus der Familie darstellen lässt.
Inhalt auf dieser Seite
Definition zur linearen Abhängigkeit
Lineare Abhängigkeit ist formal durch die folgende Implikation definiert:
Die Familie $(\overrightarrow{v_1},\ldots,\overrightarrow{v_n})$ ist linear unabhängig, wenn gilt:
\begin{align}
&\lambda_1\overrightarrow{v_1}+\lambda_2\overrightarrow{v_2}+\ldots+\lambda_n\overrightarrow{v_n}=\overrightarrow{0}\quad\lambda_1=\ldots=\lambda_n=0
\end{align}
Andernfalls ist $(\overrightarrow{v_1},\ldots,\overrightarrow{v_n})$ linear abhängig.
Diese Definition lässt sich in folgende Darstellung umschreiben:
\begin{align*}
{\lambda_1\overrightarrow{v_1}+\lambda_2\overrightarrow{v_2}+\ldots+\lambda_n\overrightarrow{v_n}=}&&\underbrace{\underbrace{\Bigl(\overrightarrow{v_1}\ldots\overrightarrow{v_n}\Bigr)}_{\text{Matrix}}\cdot\left(\begin{array}{c}{\lambda_1}\\{\vdots}\\{\lambda_n}\end{array}\right)=\left(\begin{array}{c}{0}\\{\vdots}\\{0}\end{array}\right)}_{\text{LGS}}& \ \Rightarrow\quad\left(\begin{array}{c}{\lambda_1}\\{\vdots}\\{\lambda_n}\end{array}\right)=\left(\begin{array}{c}{0}\\{\vdots}\\{0}\end{array}\right)\\
\text{bzw. }&&\underbrace{\underbrace{\Bigl(\overrightarrow{v_1}\ldots\overrightarrow{v_n}\Bigr)}_{\text{Matrix}}\cdot\overrightarrow{\lambda}=\overrightarrow{0}}_{\text{LGS}}& \ \Rightarrow\quad\overrightarrow{\lambda}=\overrightarrow{0}\notag
\end{align*}
Die Vektoren $\overrightarrow{v_1},\ldots,\overrightarrow{v_n}$ sind dabei die Spalten der Matrix.
Was sehen wir in dieser Darstellung?
Die Spaltenvektoren einer Matrix sind genau dann linear unabhängig, wenn das zugehörige homogene LGS eindeutig lösbar ist.
Äquivalent: Die Spaltenvektoren einer Matrix sind genau dann linear abhängig, wenn das zugehörige homogene LGS unendlich viele Lösungen besitzt.
Wichtig zu wissen:
- Ist die Matrix quadratisch, können die Spaltenvektoren l.u. oder l.a. sein
- Hat die Matrix mehr Zeilen als Spalten (also die Anzahl der Spaltenvektoren ist kleiner als die Anzahl ihrer Einträge), können die Spaltenvektoren l.u. oder l.a. sein
- Hat die Matrix mehr Spalten als Zeilen (also die Anzahl der Spaltenvektoren ist größer als die Anzahl ihrer Einträge), sind die Spaltenvektoren l.a.!
Ab hier sollte dir nun klar sein, dass
- eine LK eines Vektors durch eine l.u. Familie von Vektoren immer eindeutig ist
- eine LK eines Vektors durch eine l.a. Familie von Vektoren immer mehrdeutig ist
Schnelltests zur linearen Unabhängigkeit und linearen Abhängigkeit
Es gibt einige Methoden (wir haben diese einfach „Schnelltests“ genannt), mit denen wir eine Familie von Vektoren auf lineare (Un)Abhängigkeit überprüfen können.
Möglicherweise darfst du diese Schnelltests in deiner Mathematik-Veranstaltung nicht offiziell zur Argumentation benutzen. Sie dienen dir allerdings trotzdem enorm fürs Verständnis!
- Wenn der Nullvektor in einer Familie enthalten ist, ist diese immer l.a.
Familie $\left(\left(\begin{array}{c}{1}\\{2}\\{1}\end{array}\right),\left(\begin{array}{c}{0}\\{1}\\{-5}\end{array}\right),\left(\begin{array}{c}{0}\\{0}\\{0}\end{array}\right)\right)$ ist l.a.,\quad Familie $\left(\left(\begin{array}{c}{0}\\{0}\end{array}\right),\left(\begin{array}{c}{1}\\{0}\end{array}\right)\right)$ ist l.a.,\quad\ldots[/latex]
- Wenn eine Familie nur aus einem Vektor ($\neq\overrightarrow{0}$) besteht, dann ist diese l.u.
Familie $\left(\left(\begin{array}{c}{3}\\{2}\\{1}\end{array}\right)\right)$ ist l.u.,\quad Familie $\left(\left(\begin{array}{c}{1}\\{1}\end{array}\right)\right)$ ist l.u.,\quad\ldots[/latex]
- Wenn eine Familie aus zwei Vektoren besteht und diese beiden parallel zueinander stehen bzw. Vielfache sind, ist die Familie l.a.
Familie $\left(\left(\begin{array}{c}{-1}\\{4}\\{2}\end{array}\right),\left(\begin{array}{c}{2}\\{-8}\\{-4}\end{array}\right)\right)$ ist l.a., da die Vektoren Vielfache sind: $-2\cdot\left(\begin{array}{c}{-1}\\{4}\\{2}\end{array}\right)=\left(\begin{array}{c}{2}\\{-8}\\{-4}\end{array}\right)$
- Wenn eine Familie l.a. ist und es werden Vektoren hinzugefügt, bleibt sie l.a.
Familie $\left(\left(\begin{array}{c}{-1}{4}{2}\end{array}\right),\left(\begin{array}{c}{2}\\{-8}\\{-4}\end{array}\right)\right)$ ist l.a. (s.o.), also ist auch $\left(\left(\begin{array}{c}{-1}\\{4}\\{2}\end{array}\right),\left(\begin{array}{c}{1}\\{7}\\{9}\end{array}\right),\left(\begin{array}{c}{2}\\{-8}\\{-4}\end{array}\right)\right)$ l.a.
- Wenn eine Familie l.u. ist und es werden Vektoren herausgenommen, bleibt sie l.u.
Familie $\left(\left(\begin{array}{c}{1}\\{3}\\{0}\end{array}\right),\left(\begin{array}{c}{1}\\{1}\\{1}\end{array}\right),\left(\begin{array}{c}{-1}\\{1}\\{0}\end{array}\right)\right)$ ist l.u., also ist auch $\left(\left(\begin{array}{c}{1}\\{3}\\{0}\end{array}\right),\left(\begin{array}{c}{1}\\{1}\\{1}\end{array}\right)\right)$ l.u.
Erzeugendensystem
Ein Erzeugendensystem (EZS) eines Vektorraums $V$ ist eine Familie von Vektoren, die $V$ durch die Menge aller ihrer Linearkombinationen erzeugt.
Ganz allgemein ausgedrückt ist jede Familie von Vektoren ein EZS für einen entsprechenden Vektorraum. Daher ergibt die reine Frage, ob … ein EZS ist, wenig Sinn (vergleiche mit der Fragestellung bei einem UVR)
An die Anzahl der Vektoren aus der Familie sind keine Bedingungen geknüpft (sprich, ob die Familie von Vektoren l.u. oder l.a. ist, spielt keine Rolle; es dürfen sogar unendlich viele Vektoren ein EZS bilden). Sie müssen natürlich lediglich aus dem selben Vektorraum stammen.
\begin{align*}
\displaystyle \left(\left(\begin{array}{c}{1}\\{2}\\{3}\end{array}\right),\left(\begin{array}{c}{-2}\\{1}\end{array}\right)\right) \text{ kann kein EZS sein, da } (1,2,3)^T\in\mathbb{R}^3 \text{ und } (-2,1)^T\in\mathbb{R}^2 \text{ Vektoren aus verschiedenen Vektorräumen sind. }
\end{align*}
Basis
Eine Basis ist ein linear unabhängiges EZS. Vektoren aus einer Basis werden auch als Basisvektoren bezeichnet.
Anders als bei einem allgemeinen EZS, ergibt die Frage, ob … eine Basis ist, schon mehr Sinn. Denn eine Basis ist eine Familie aus l.u. Vektoren. Dennoch wird auch hier meistens gefragt: „Ist … eine Basis von …?“
Dimension
Die Dimension eines Vektorraums $V$ ($\dim(V)$) entspricht der Anzahl an linear unabhängigen Vektoren, die diesen Raum durch Linearkombinationen erzeugen können.
Später werden wir die Dimension durch den Rang leicht bestimmen können!
Wir können auch sagen: Die Dimension eines Vektorraums $V$ entspricht der Anzahl an Vektoren in einer zugehörigen Basis von $V$.
Koordinaten
Der Begriff „Koordinaten“ sollte dir schon bezüglich der Lagebeschreibung von Punkten etwas sagen. Im $\mathbb{R}^2$ lesen wir die Koordinaten eines Punktes an der $x$– und $y$-Achse ab, um zu beschreiben, wo sich der Punkt befindet. Im $\mathbb{R}^3$ äquivalent noch zusätzlich mit der $z$-Achse dazu. Wenn wir hinterfragen, warum wir das genau wie gerade beschrieben tun, kommen wir (in Vektorschreibweise) zu:
\begin{align*}
\left(\begin{array}{c}{2}\\{3}\\{4}\end{array}\right)=\underbrace{\left(\begin{array}{c}{2}\\{0}\\{0}\end{array}\right)}_{\ast^1}+\underbrace{\left(\begin{array}{c}{0}\\{3}\\{0}\end{array}\right)}_{\ast^2}+\underbrace{\left(\begin{array}{c}{0}\\{0}\\{4}\end{array}\right)}_{\ast^3}=\underbrace{\textbf{2}\cdot\left(\begin{array}{c}{1}\\{0}\\{0}\end{array}\right)+\textbf{3}\cdot\left(\begin{array}{c}{0}\\{1}\\{0}\end{array}\right)+\textbf{4}\cdot\left(\begin{array}{c}{0}\\{0}\\{1}\end{array}\right)}_{\ast^4}
\end{align*}
$\ast^1$: Wir gehen im Raum 2 Einheiten in $x$-, 0 Einheiten in $y$– und 0 Einheiten in $z$-Richtung.
$\ast^2$: Wir gehen im Raum 0 Einheiten in $x$-, 3 Einheiten in $y$– und 0 Einheiten in $z$-Richtung.
$\ast^3$: Wir gehen im Raum 0 Einheiten in $x$-, 0 Einheiten in $y$– und 4 Einheiten in $z$-Richtung.
$\ast^4$: Darstellung als $\textbf{Koordinaten}$ $\cdot$ Vektor
Auf der $x$-, $y$– (und $z$-)Achse befinden sich also Basisvektoren (hier die Standardbasis), mit denen wir die Lage von Punkten beschreiben können.
Koordinaten eines Punktes/Vektors müssen wir streng genommen immer in Bezug zu einem EZS angeben. Wenn dies nicht der Fall ist, ist das EZS immer die Standardbasis.
Nun ist es natürlich extrem wichtig, mit welchen Vektoren wir einen Punkt erreichen. An dieser Stelle merken wir uns:
- Koordinaten eines Punktes bzgl. einer Basis sind eindeutig!
- Koordinaten eines Punktes bzgl. eines EZS (welches keine Basis ist!) sind mehrdeutig!
Lineare Hülle
Die Lineare Hülle (auch der Spann oder das Erzeugnis genannt) eines Erzeugendensystems ist ein Untervektorraum des Vektorraums $V$, aus dem die Vektoren im Erzeugendensystem stammen. Visualisiert sieht dies wie folgt aus:
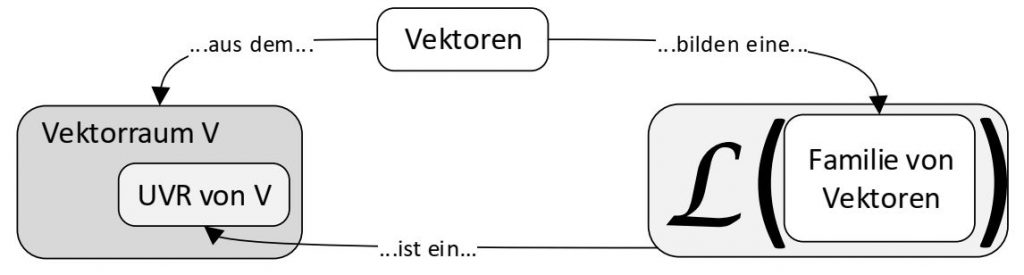
Als Gleichung in „Wortlaut“ ist das:
\begin{align}
L \ \text{(Familie von Vektoren aus V)}=\text{UVR von }V\quad\text{oder}\quad L \ (\text{EZS aus V})=\text{UVR von }V
\end{align}
Die lineare Hülle einer Familie von Vektoren entsteht durch die Menge aller möglichen Linearkombinationen der Vektoren:
\begin{align}
L \ (\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots)&=\text{span}\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots)=\left\langle\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots\right\rangle\\
&:=\{\lambda_1\overrightarrow{v}_1+\lambda_2\overrightarrow{v}_2+\ldots\ |\ \lambda_1,\lambda_2,\ldots\in\mathbb{R}\}
\end{align}
\begin{align}
L \ (\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots), \ \text{span}(\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots) \text{ und } \left\langle\overrightarrow{v}_1,\overrightarrow{v}_2,\ldots\right\rangle \text{ sind also nur Kurzschreibweisen! }
\end{align}
Zusammenhänge EZS – L(EZS)
Diese Zusammenhänge sind für unser Verständnis extrem wichtig! Im Prinzip geht es hier immer darum, ob sich die Dimension der linearen Hülle erhöht/verringert (dann ändert sich die lin. Hülle) oder ob die Dimension gleich bleibt (dann bleibt auch die lin. Hülle gleich).
Das natürlich immer ausgehend von einer bestimmten lin. Hülle. Natürlich können zwei verschiedene lin. Hüllen die gleiche Dimension haben!
- Wenn ein EZS l.u. ist und es wird ein Vektor aus dem EZS herausgestrichen, ändert sich die lineare Hülle (Dimension verringert sich um 1)
- Wenn ein EZS l.u. ist und es wird ein Vektor zu dem EZS hinzugefügt, kommt es darauf an:
- Ist der hinzugefügte Vektor eine LK von den ursprünglichen Vektoren, so wird das EZS l.a. aber die lineare Hülle ändert sich nicht (denn der neue Vektor lässt sich durch die ursprünglichen als LK darstellen und erhöht somit die Dimension der lin. Hülle nicht!)
- Ist der hinzugefügte Vektor keine LK von den ursprünglichen Vektoren, so bleibt das EZS l.u., aber die lineare Hülle ändert sich (Dimension erhöht sich um 1)
- Wenn ein EZS l.a. ist und es wird ein Vektor aus dem EZS herausgestrichen, kann sich die lineare Hülle ändern, sie muss aber nicht. Es kommt darauf an:
- Lässt sich der herausgestrichene Vektor als LK der noch übrigen Vektoren darstellen, dann ändert sich die lin. Hülle nicht (Dimension bleibt gleich, denn der herausgestrichene Vektor trug nichts zur lin. Hülle bei!)
- Lässt sich der herausgestrichene Vektor nicht als LK der noch übrigen Vektoren darstellen, dann ändert sich die lin. Hülle (Dimension verringert sich um 1)
- Wenn ein EZS l.a. ist und es wird ein Vektor zu dem EZS hinzugefügt, kann sich die lineare Hülle ändern, sie muss aber nicht. Es kommt darauf an:
- Lässt sich der hinzugefügte Vektor als LK der anderen Vektoren darstellen, dann ändert sich die lin. Hülle nicht (Dimension bleibt gleich, denn der hinzugefügte Vektor trägt nichts zur lin. Hülle bei!)
- Lässt sich der hinzugefügte Vektor nicht als LK der anderen Vektoren darstellen, dann ändert sich die lin. Hülle (Dimension erhöht sich um 1)
Du solltest merken, dass viele Aussagen einfacher und eindeutiger von der Hand gehen, wenn ein EZS eine Basis ist. Basen sind daher „gute“ Erzeugendensysteme.
Prüfen, ob eine gegebene Familie von Vektoren $(\overrightarrow{v_1},\ldots,\overrightarrow{v_n})$ ein EZS eines Vektorraums $V$ ist (also ob L $\ (\overrightarrow{v_1},\ldots,\overrightarrow{v_n})=V$ gilt):
Zuerst: (Originales) EZS von $V$ ausfindig machen (kleinstmögliche Anzahl an Vektoren). Oft ist das schon gegeben. Dann müssen die folgenden beiden Punkte erfüllt sein:
- Jeder Vektor aus dem EZS von $V$ muss eine LK der Vektoren der Familie $(\overrightarrow{v_1},\ldots,\overrightarrow{v_n})$ sein.
- $\dim(V)=\dim\bigl(L \ (\overrightarrow{v_1},\ldots,\overrightarrow{v_n})\bigr)$
Gegeben ist ein Vektorraum $V=\left\{s\left(\begin{array}{c}{1}\\{1}\\{2}\end{array}\right)+t\left(\begin{array}{c}{0}\\{-3}\\{1}\end{array}\right)\ \Bigl|\Bigr.\ s,t\in\mathbb{R}\right\}$
Gilt $L \ \left(\left(\begin{array}{c}{2}\\{-1}\\{5}\end{array}\right),\left(\begin{array}{c}{1}\\{7}\\{0}\end{array}\right),\left(\begin{array}{c}{4}\\{-5}\\{11}\end{array}\right)\right)=V$?
Das EZS von $V$ ist ablesbar: $\left(\left(\begin{array}{c}{1}\\{1}\\{2}\end{array}\right),\left(\begin{array}{c}{0}\\{-3}\\{1}\end{array}\right)\right)$
Jetzt müssen die folgenden LGS lösbar sein:
\begin{align*}
\underbrace{\underbrace{\begin{pmatrix} % 3×3
2 & 1 & 4 \\
-1 & 7 & -5 \\
5 & 0 & 11
\end{pmatrix}}_{A}\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right) = \left(\begin{array}{c}{1}\\{1}\\{2}\end{array}\right)}_{\text{LGS 1}}\quad\text{und}\quad\underbrace{\underbrace{\begin{pmatrix} % 3×3
2 & 1 & 4 \\
-1 & 7 & -5 \\
5 & 0 & 11
\end{pmatrix}}_{A}\left(\begin{array}{c}{x_1}\\{x_2}\\{x_3}\end{array}\right) = \left(\begin{array}{c}{0}\\{-3}\\{1}\end{array}\right)}_{\text{LGS 2}}
\end{align*}
Da es hier nur um die Lösbarkeit geht und nicht um eine konkrete Lösung, reicht der Gauß-Algorithmus bis zur ZSF. Außerdem können wir beide Rechnungen gleichzeitig durchführen, denn die Überführung der Matrix in ZSF ist bei beiden LGS gleich:
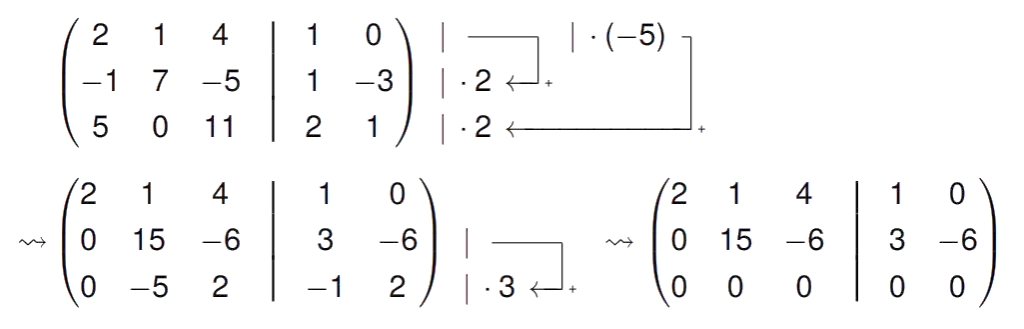
Wir sehen, dass sowohl LGS 1 als auch LGS 2 lösbar sind (mehrdeutig).
\begin{align*}
\text{Da }\left(\left(\begin{array}{c}{1}\\{1}\\{2}\end{array}\right),\left(\begin{array}{c}{0}\\{-3}\\{1}\end{array}\right)\right) \text{ l.u. (2 Vektoren und keine Vielfachen), ist } \text{dim}(V)=2.
\end{align*}
Wir lesen ab, dass $\text{rg(A)}=2$ gilt und damit $\dim(L\left(\left(\begin{array}{c}{2}\\{-1}\\{5}\end{array}\right),\left(\begin{array}{c}{1}\\{7}\\{0}\end{array}\right),\left(\begin{array}{c}{4}\\{-5}\\{11}\end{array}\right)\right)=2$
Also gilt $L\left(\left(\begin{array}{c}{2}\\{-1}\\{5}\end{array}\right),\left(\begin{array}{c}{1}\\{7}\\{0}\end{array}\right),\left(\begin{array}{c}{4}\\{-5}\\{11}\end{array}\right)\right)=V$.